Когда мы вычисляем предел в точке 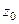 , он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела
, он может быть конечным, бесконечным либо не существовать. Аналогично этому, подобные ситуации могут быть и при вычислении предела 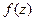 при
при 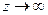 . Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.
. Бесконечность не является точкой в плоскости, тем не менее, тип такого объекта как «бесконечно-удалённая точка» можно тоже классифицировать как и типы особых точек, с помощью предела.
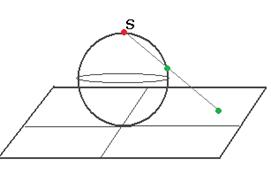
Существует геометрическая модель, в которой бесконечно-удалённая точка присутствует на равных с другими точками. Поместим сферу над плоскостью в начало координат. Если от верхней точки S провести любую наклонную прямую, то она 1 раз пересечётся со сферой и 1 раз с плоскостью. Таким образом, каждой точке комплексной плоскости можно однозначно поставить в соответствие точку на сфере. При этом единственная точка, для которой нет образа на плоскости - это точка S. Она соответствует горизонтальной касательной, и можно поставить ей в соответствие «бесконечно удалённую точку».
Классификация 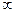 как особой точки происходит аналогично, как и было для точки
как особой точки происходит аналогично, как и было для точки 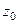 :
:
| Название | Устранимая особая точка | Полюс | Существенно-особая точка |
| При каком условии | 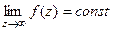
| 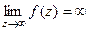
| 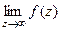 не существует
не существует
|
| Пример | 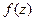 = = 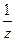
| 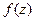 = = 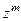
| 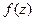 = = 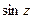
|
Только в данном случае наоборот, полюс если степень m в числителе, а не в знаменателе. Например, для 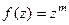 полюс порядка m.
полюс порядка m.
В задачах можно делать замену 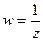 и таким образом сводить изучение
и таким образом сводить изучение 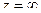 к изучению поведения функции в точке
к изучению поведения функции в точке 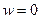 .
.
Пример. Определить тип точки 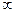 для
для 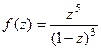 .
.
Решение. Сделаем замену 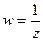 , т.е. После этого функция изменит вид так:
, т.е. После этого функция изменит вид так: 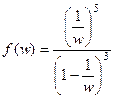 =
= 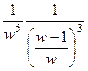 =
= 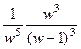 .
.
Попутно заметим, что 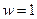 а значит и
а значит и 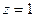 - полюс 3-го порядка.
- полюс 3-го порядка.
Для точки 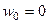 , соответствующей
, соответствующей 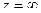 , видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить
, видим нуль 3-го порядка в числителе и 5-го порядка в знаменателе. Сократив дробь, можно получить 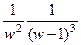 . Тогда видно, что
. Тогда видно, что 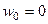 полюс 2-го порядка, а значит,
полюс 2-го порядка, а значит, 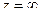 полюс 2-го порядка.
полюс 2-го порядка.
Пример. Определить тип точки 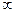 для
для 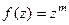 .
.
Решение. Сделаем замену 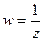 , т.е. После этого функция станет
, т.е. После этого функция станет 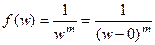 , то есть
, то есть 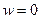 полюс порядка m, значит
полюс порядка m, значит 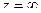 полюс порядка m.
полюс порядка m.
Пример. Определить тип точки 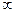 для
для 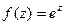 .
.
Решение. Сделаем замену 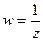 , т.е. После этого
, т.е. После этого 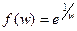 .
.
Если устремить 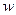 к 0 со стороны положительной полуоси, то получается
к 0 со стороны положительной полуоси, то получается 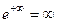 . Если со стороны отрицательной полуоси, то
. Если со стороны отрицательной полуоси, то 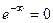 . А если со стороны мнимой оси, то предел вообще не существует: при
. А если со стороны мнимой оси, то предел вообще не существует: при 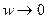 ,
, 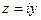 , и при этом
, и при этом 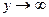 , при этом
, при этом 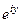 =
= 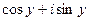 , т.е. при
, т.е. при 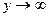 не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует. Вывод: предел в точке
не существует предел ни действительной, ни мнимой части. Итак, приближаясь к (0,0) на плоскости с разных сторон, получаем разные результаты, а при приближении по некоторым траекториям предел даже не существует. Вывод: предел в точке 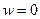 не существует,
не существует, 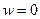 а значит
а значит 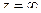 это существенно-особая точка.
это существенно-особая точка.
Определение. Пусть 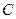 замкнутый контур, внутри него точка
замкнутый контур, внутри него точка 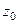 , на самом контуре и внутри него нет особых точек, кроме
, на самом контуре и внутри него нет особых точек, кроме 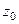 . Тогда интеграл
. Тогда интеграл 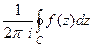 называется вычетом функции
называется вычетом функции 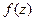 в точке
в точке 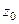 и обозначается
и обозначается 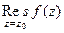 .
.
Теорема. Если 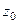 простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета:
простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета: 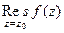 =
= 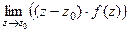 .
.
Доказательство (ДОК 23). Если 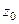 полюс 1-го порядка, то функцию можно представить в виде:
полюс 1-го порядка, то функцию можно представить в виде: 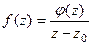 , тогда верно
, тогда верно 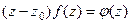 . В то же время по интегральной формуле Коши:
. В то же время по интегральной формуле Коши: 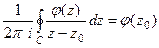 .Тогда
.Тогда 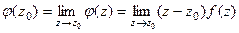 .
.
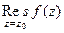 =
= 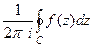 =
= 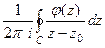 =
= 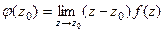 .
.
Что и требовалось доказать.
Выведем формулу для полюса порядка m.
Теорема. Если 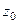 - полюс порядка m, то верна формула вычисления вычета:
- полюс порядка m, то верна формула вычисления вычета: 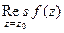 =
= 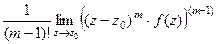 .
.
Доказательство (ДОК 24). Запишем обобщённую формулу Коши для какой-нибудь функции 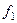 , т.к. обозначение
, т.к. обозначение 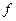 у нас уже использовано, оно будет применяться ко всей функции, которая в интеграле.
у нас уже использовано, оно будет применяться ко всей функции, которая в интеграле.
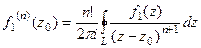 . Но ведь мы можем сделать такую замену индекса:
. Но ведь мы можем сделать такую замену индекса: 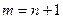 и переписать формулу в виде
и переписать формулу в виде
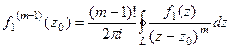 или эквивалентно:
или эквивалентно: 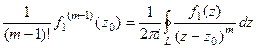 . Пусть
. Пусть 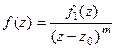 . Тогда
. Тогда
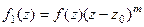 , а интегральная формула Коши запишется в виде:
, а интегральная формула Коши запишется в виде: 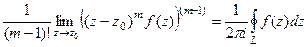 =
= 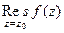 . Правая часть этой формулы по определению как раз и равна вычету
. Правая часть этой формулы по определению как раз и равна вычету 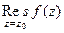 .
.
Пример. Найти вычет 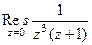 .
.
Решение. Здесь точка 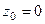 полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:
полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:
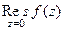 =
= 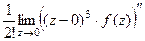 . Итак,
. Итак, 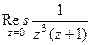 =
=  =
= 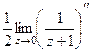 =
= 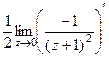 =
= 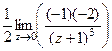 =
= 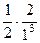 = 1.
= 1.
Пример. Найти вычет 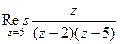 .
.
Решение. Здесь точка 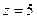 полюс 1 порядка. Поэтому
полюс 1 порядка. Поэтому
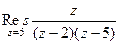 =
= 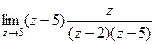 =
= 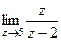 =
= 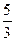 .
.
Пример. Найти вычет 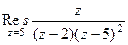 .
.
Решение. Здесь точка 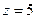 полюс 2 порядка. Поэтому
полюс 2 порядка. Поэтому
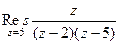 =
= 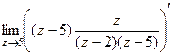 =
= 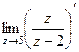 =
=
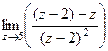 =
= 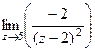 =
= 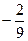 .
.
ЛЕКЦИЯ 7. 14.10.2019
ЛЕКЦИЯ 8. 21.10.2019
ЛЕКЦИЯ 9. 28.10.2019
ЛЕКЦИЯ 10. 11.11.2019
ЛЕКЦИЯ 11. 18.11.2019
ЛЕКЦИЯ 12. 25.11.2019
ЛЕКЦИЯ 13. 02.12.2019
ЛЕКЦИЯ 14. 09.12.2019
ЛЕКЦИЯ 15. 16.12.2019
ЛЕКЦИЯ 16. 23.12.2019
Дата: 2019-11-01, просмотров: 278.