Возможны разные подходы к определению понятия интеграла от комплексной функции. Так, например,  - функции двух переменных, тогда можно вычислять кратные интегралы от них по некоторой плоской области, и объединять результаты в комплексное число вида
- функции двух переменных, тогда можно вычислять кратные интегралы от них по некоторой плоской области, и объединять результаты в комплексное число вида 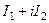 . Однако в качестве основного всё же исторически был принят метод интегрирования по кривой, именно при таком подходе возможно введение понятия первообразной
. Однако в качестве основного всё же исторически был принят метод интегрирования по кривой, именно при таком подходе возможно введение понятия первообразной 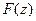 , а также получают применение многие факты из теории векторного поля. Итак, определение интеграла и метод его вычисления:
, а также получают применение многие факты из теории векторного поля. Итак, определение интеграла и метод его вычисления:
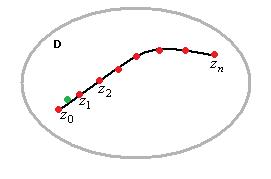
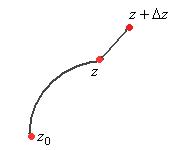
Определение. Пусть в области  задана некоторая функция
задана некоторая функция 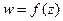 (не обязательно аналитическая), и в области
(не обязательно аналитическая), и в области  расположена кусочно-гладкая кривая
расположена кусочно-гладкая кривая  (не обязательно замкнутая). Введём разбиение кривой на n частей с помощью (n-1) внутренних точек. Таким образом, получилась последовательность точек
(не обязательно замкнутая). Введём разбиение кривой на n частей с помощью (n-1) внутренних точек. Таким образом, получилась последовательность точек 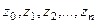 , расположенных по порядку на кривой, где
, расположенных по порядку на кривой, где 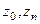 - начальная и конечная точки. Обозначим
- начальная и конечная точки. Обозначим 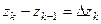 . Выберем на каждом участке дуги какую-то точку
. Выберем на каждом участке дуги какую-то точку 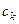 и составим интегральную сумму:
и составим интегральную сумму: 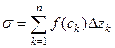 . Предел интегральных сумм при измельчении разбиения, т.е. при
. Предел интегральных сумм при измельчении разбиения, т.е. при 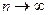 , называется интегралом от функции
, называется интегралом от функции 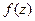 по кривой
по кривой 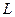 и обозначается
и обозначается 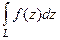 .
.
Метод вычисления. При вычислении необходимо разбить на действительную и мнимую части как функцию, так и дифференциал, затем раскрыть скобки и получить 4 слагаемых. Но их можно объединить по два, в двух из них нет мнимой единицы, а в двух она есть:
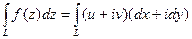 =
= 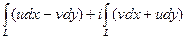 .
.
Таким образом, при вычислении всё сводится к двум криволинейным интегралам 2-го рода от векторных полей 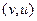 и
и 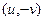 , а мнимая единица умножается на второй из них, при этом в самих вычислениях она фактически не участвует.
, а мнимая единица умножается на второй из них, при этом в самих вычислениях она фактически не участвует.
Некоторые свойства.
1. Линейность 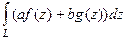 =
=  .
.
2. Если кривая АС разбита на две части некоторой точкой В, то: 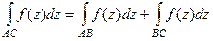
3. 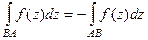 .
.
4. Если 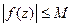 то
то 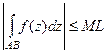 , где
, где  - длина кривой АВ.
- длина кривой АВ.
Пример. Вычислить интеграл 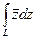 :
:
А) по прямолинейному отрезку от 0 до  .
.
Б) по параболе от 0 до  .
.
Решение.
А) 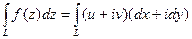 =
= 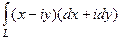 =
=
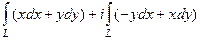 , далее вычисляем 2 криволинейных интеграла по отрезку, на котором
, далее вычисляем 2 криволинейных интеграла по отрезку, на котором 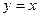 , заменяем
, заменяем 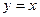 ,
, 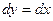 .
.
При этом 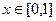 .
. 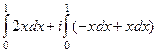 =
= 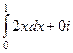 =
= 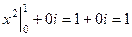 .
.
Б) Исходное раскрытие скобок происходит так же, как и в прошлом случае: 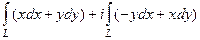 но теперь линия
но теперь линия  это не отрезок, заданный явным уравнением
это не отрезок, заданный явным уравнением 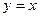 , а парабола, заданная явным уравнением
, а парабола, заданная явным уравнением 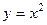 . Поэтому заменяем
. Поэтому заменяем 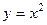 ,
, 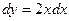 .
.
 =
= 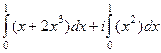 =
=
 =
=  .
.
Ответ. по отрезку: 1, по параболе:  .
.
Как видим, в зависимости от формы кривой могут получиться разные ответы, но это здесь потому, что функция не аналитическая, она содержит 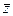 , а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию
, а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию 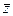 в составе функции, то есть тому, что
в составе функции, то есть тому, что 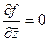 .
.
Пример. Вычислить 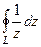 , где
, где 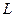 - окружность радиуса
- окружность радиуса  вокруг точки 0.
вокруг точки 0.
Решение. Представим функцию в виде 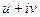 . Движение по окружности можно задать формулами:
. Движение по окружности можно задать формулами:
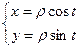
В этом случае 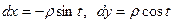 . Тогда
. Тогда
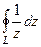 =
= 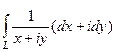 =
= 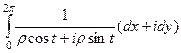 =
=
домножим на сопряжённое, 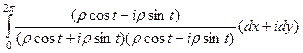 =
=
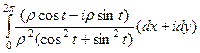 =
= 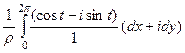 =
=
 =
= 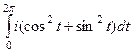 =
=
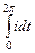 =
= 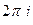 .
.
Пример. Вычислить 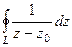 , где
, где  - окружность радиуса
- окружность радиуса  вокруг точки
вокруг точки 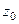 .
.
Решение. Изучим при этом ещё более короткий способ с более компактной записью. Представим 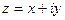 =
= 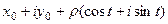 =
= 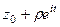 . Тогда
. Тогда 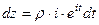 .
.
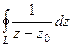 =
=  =
= 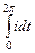 =
= 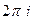 .
.
ЛЕКЦИЯ 5. 30.09.2019
Теорема 1. Если  замкнутый контур, внутри которого во всех точках
замкнутый контур, внутри которого во всех точках  является аналитической, то
является аналитической, то 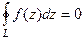 .
.
(ДОК 14). Доказательство. 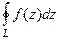 =
= 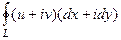 =
=
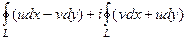 в двух этих интегралах - циркуляция двух векторных полей
в двух этих интегралах - циркуляция двух векторных полей 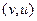 и
и 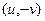 , они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем
, они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем 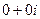 .
.
Теорема 2. Если 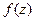 является аналитической во всех точках некоторой области
является аналитической во всех точках некоторой области 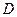 , граница которой односвязна, то интеграл от функции
, граница которой односвязна, то интеграл от функции 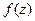 не зависит от пути, то есть имеет одно и то же значение для любой кривой
не зависит от пути, то есть имеет одно и то же значение для любой кривой 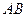 , соединяющей пару точек
, соединяющей пару точек 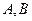 .
.
(ДОК 15). Доказательство. Аналогично прошлой теореме,
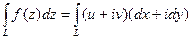 =
= 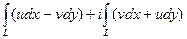 .
.
Криволинейные интегралы 2 рода от векторных полей 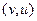 и
и 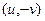 не зависят от пути, что доказано ранее в главе «теория поля».
не зависят от пути, что доказано ранее в главе «теория поля».
Так как для аналитической функции интеграл не зависит от пути, то для аналитической функции оказывается возможным ввести понятие первообразной. Введём в рассмотрение такую функцию: 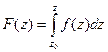 которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки
которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки 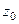 . Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей
. Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей 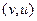 и
и 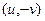 . Докажем, что построенная таким образом функция является первообразной.
. Докажем, что построенная таким образом функция является первообразной.
Теорема 3. Функция 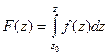 является первообразной от функции
является первообразной от функции  .
.
(ДОК 16). Доказательство.
Докажем, что производная от 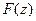 равна
равна 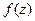 .
.
По определению производной, 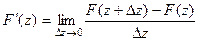 .
.
Распишем разность в числителе более подробно.
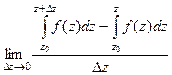 =
= 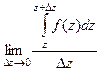 .
.
потому что по свойству 2, в числителе сокращается интеграл по той части, которая от 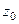 до
до 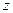 , и остаётся только от
, и остаётся только от 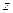 до
до 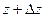 .
.
Распишем более подробно действительную и мнимую часть в интеграле.
 =
= 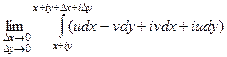
Так как векторные поля в этих криволинейных интегралах потенциальны, то можно пройти по любому пути от точки 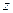 до
до 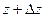 , в частности, по ломаной, где один участок горизонтальный, другой вертикальный (как это делали когда-то при поиске потенциала).
, в частности, по ломаной, где один участок горизонтальный, другой вертикальный (как это делали когда-то при поиске потенциала).
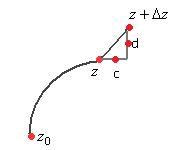
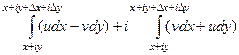 =
= 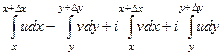
Получилось 4 интеграла, каждый от действительной функции. Для непрерывной функции действительного переменного верна теорема о среднем, т.е. свойство: 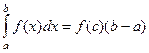 , значит, для этих 4 интегралов существуют такие точки
, значит, для этих 4 интегралов существуют такие точки 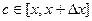 ,
, 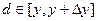 что выполняется:
что выполняется:
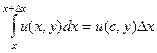 ,
, 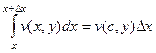 ,
,
 ,
, 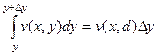
причём при 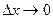 точка
точка 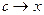 , ведь она находится на отрезке, который стягивается в одну точку, в свою левую границу, аналогично
, ведь она находится на отрезке, который стягивается в одну точку, в свою левую границу, аналогично 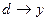 при
при 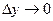 .
.
Тогда 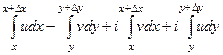 =
=
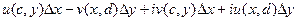 , в пределе это стремится к
, в пределе это стремится к
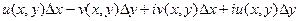 , что равно
, что равно
 =
= 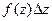 . Вспомним, что это изначально был числитель в дроби
. Вспомним, что это изначально был числитель в дроби  , и тогда
, и тогда 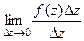 =
= 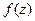 .
.
Теорема 4. Для аналитической на кривой  функции верна формула Ньютона-Лейбница:
функции верна формула Ньютона-Лейбница:  .
.
(ДОК 17). Доказательство. По построению первообразной,
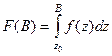 и
и 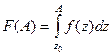 .
.
Но тогда 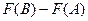 =
= 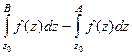 а тогда по 3-му свойству
а тогда по 3-му свойству
это 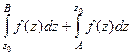 , что равно интегралу по кривой, проходящей от
, что равно интегралу по кривой, проходящей от  до
до  (через точку
(через точку  ).
).
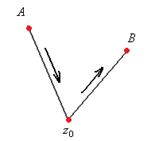
Тогда  =
= 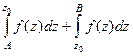 =
= 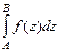 т.к. по свойству 2, их можно объединить. Итак,
т.к. по свойству 2, их можно объединить. Итак, 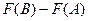 =
= 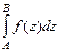 .
.
Пример. Вычислить 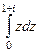 от 0 до
от 0 до 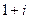 двумя способами:
двумя способами:
А) без формулы Б) по формуле Ньютона-Лейбница.
Решение.
А) 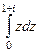 =
= 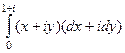 =
= 
Пусть точки 0 и 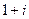 соединены по прямой
соединены по прямой  (вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда
(вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда 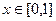 ,
, 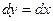 , и
, и
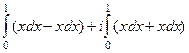 =
= 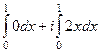 =
= 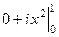 =
= 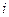 .
.
Б) По формуле: 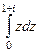 =
= 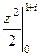 =
=  =
=  =
= 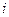 .
.
Интегральная формула Коши
Заметим, что в последнем примере в конце прошлой лекции  сократилось и ответ вообще не зависел от
сократилось и ответ вообще не зависел от  - радиуса окружности. То есть получается, при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
- радиуса окружности. То есть получается, при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
Теорема 1. (Интегральная теорема Коши).
Пусть  некоторый замкнутый контур,
некоторый замкнутый контур, 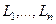 - n замкнутых непересекающихся контуров, лежащих внутри
- n замкнутых непересекающихся контуров, лежащих внутри  . Функция
. Функция 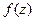 является аналитической на всех этих контурах, а также внутри
является аналитической на всех этих контурах, а также внутри 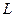 , но вне
, но вне 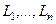 . Тогда
. Тогда  .
.
Доказательство (ДОК 18).
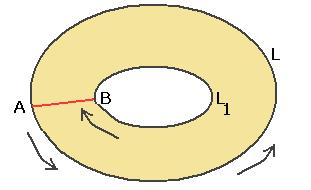
Для того, чтобы лучше понять идею доказательства, рассмотрим сначала ситуацию, когда внутри 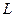 расположен один контур
расположен один контур 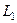 , то есть оласть аналитичности - кольцо. Можно взять какую-либо пару точек
, то есть оласть аналитичности - кольцо. Можно взять какую-либо пару точек 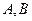 на
на  и
и 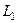 соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей:
соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей: 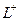 ,
, 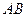 ,
, 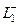 ,
, 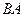 внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено
внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено 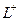 , затем переходя на внутренний контур по
, затем переходя на внутренний контур по 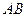 , затем двигаясь по внутреннему в противоположном направлении (
, затем двигаясь по внутреннему в противоположном направлении (  ), и возвращаясь по
), и возвращаясь по  снова на внешний контур. Чертёж:
снова на внешний контур. Чертёж:
Но если комбинированный контур окружает область аналитичности, то интеграл по нему равен 0.
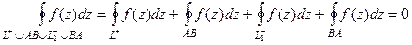 .
.
При этом интегралы по 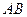 и
и  и так взаимно уничтожаются, поэтому
и так взаимно уничтожаются, поэтому 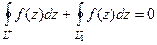 . Но если сменить направление движение по внутреннему контуру
. Но если сменить направление движение по внутреннему контуру 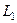 , то интеграл по нему сменил бы знак, тогда:
, то интеграл по нему сменил бы знак, тогда: 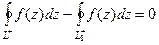
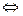
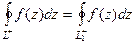 .
.
Таким образом, интегралы по  и
и 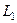 одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.
одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.
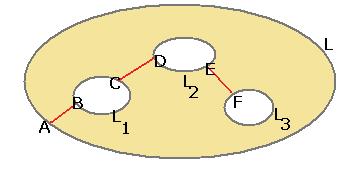
Если внутри  несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком
несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком 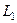 с
с 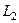 , затем
, затем  с
с 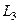 и так далее, до номера n.
и так далее, до номера n.
Теорема 2. (Интегральная формула Коши).
Пусть 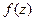 является аналитической на контуре
является аналитической на контуре  и внутри него, точка
и внутри него, точка 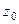 лежит внутри
лежит внутри 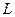 . Тогда
. Тогда 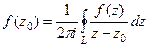 .
.
Доказательство (ДОК 19).
В рассмотренном примере в конце прошлой лекции мы вычислили 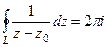 , то есть верно
, то есть верно 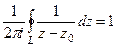 . Но мы можем домножить это равенство на любую комплексную константу, и тогда:
. Но мы можем домножить это равенство на любую комплексную константу, и тогда:  . Впрочем, тогда это же верно и для константы
. Впрочем, тогда это же верно и для константы 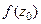 : получаем
: получаем 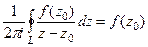 . Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что
. Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что  , или то же самое, что
, или то же самое, что 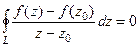 , то требуемое утверждение будет верно.
, то требуемое утверждение будет верно.
Рассмотрим функцию  . Это функция, которая участвует в определении предела, ведь
. Это функция, которая участвует в определении предела, ведь 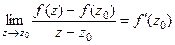 .
.
Таким образом,  , то есть
, то есть  имеет конечный предел в точке
имеет конечный предел в точке 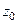 , а это значит, что она ограничена в окрестности этой точки,
, а это значит, что она ограничена в окрестности этой точки, 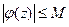 . По теореме 1 (интегральная теорема Коши), интеграл по
. По теореме 1 (интегральная теорема Коши), интеграл по  можно заменить на интеграл по любой малой окружности
можно заменить на интеграл по любой малой окружности 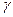 радиуса
радиуса 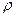 , лежащей внутри
, лежащей внутри 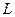 , результат при этом не изменится. Тогда
, результат при этом не изменится. Тогда  =
= 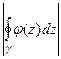
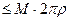 , где
, где 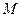 - максимальное значение модуля функции,
- максимальное значение модуля функции, 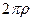 - длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого
- длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого  . То есть
. То есть 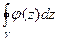 меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть
меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть 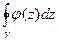 =
= 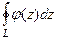 =
= 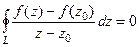 . Значит,
. Значит, 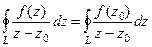 , а тогда:
, а тогда:
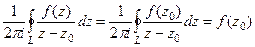 , т.е.
, т.е. 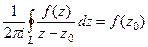 доказано в итоге.
доказано в итоге.
Интегральная формула Коши позволяет быстро вычислять интегралы по контуру вокруг точки разрыва, фактически не проводя подробное интегрирование. Достаточно убрать из знаменателя ту скобку 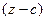 , которая соответствует этой точке разрыва, подставить в остальную функцию
, которая соответствует этой точке разрыва, подставить в остальную функцию 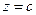 и домножить на
и домножить на 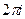 .
.
Пример. Вычислить 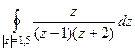 .
.
Решение. Внутри окружности радиуса 1,5 всего одна из двух точек разрыва функции, вторая снаружи. Обозначим в качестве 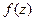 функцию без
функцию без 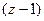 , как будто на
, как будто на 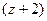 делим чуть раньше, а на
делим чуть раньше, а на 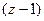 позже.
позже.
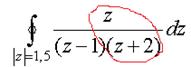
 =
=  , где
, где 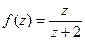 это то, что именно обозначается
это то, что именно обозначается  в интегральной формуле Коши.
в интегральной формуле Коши.
Тогда 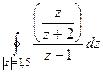 =
= 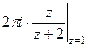 =
= 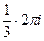 =
= 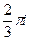 . \
. \
Ответ. 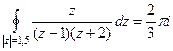 .
.
ЛЕКЦИЯ 6. 07.10.2019
Теорема 3. (Обобщённая интегральная формула Коши).
Пусть 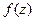 является аналитической на контуре
является аналитической на контуре  и внутри него, точка
и внутри него, точка 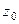 лежит внутри
лежит внутри 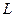 . Тогда
. Тогда  .
.
Доказательство (ДОК 20).
Продифференцируем по параметру  правую и левую часть равенства в исходной интегральной формуле Коши.
правую и левую часть равенства в исходной интегральной формуле Коши.
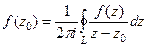 .
.
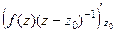 =
= 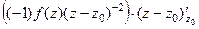 =
=  =
=  =
= 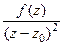 .
.
Таким образом, 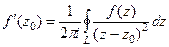 .
.
Следующая производная от 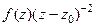 равна
равна
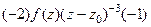 =
= 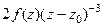 . Аналогично следующая (тертья от исходной функции) равна
. Аналогично следующая (тертья от исходной функции) равна 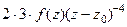 , далее по индукции для n-й производной получим
, далее по индукции для n-й производной получим 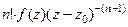 =
=  . Тогда
. Тогда 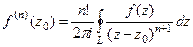 .
.
Рассмотрим примеры, похожие на предыдущий, но в которых будет 2 или 3 степень скобки 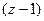 . По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять
. По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять 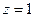 . А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет
. А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет 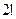 .
.
Пример. Вычислить 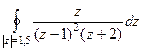 .
.
Решение. 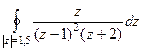 =
= 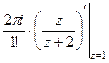 =
=  =
= 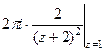 =
=  =
= 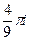 .
.
Ответ. 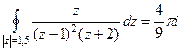 .
.
Пример. Вычислить 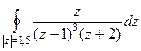 .
.
Решение. 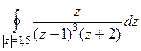 =
= 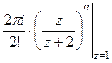 =
=  =
=
 =
= 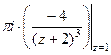 =
=  =
= 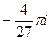 .
.
Ответ. 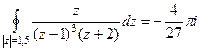 .
.
Лемма Доказать, что 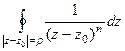 = 0 для любого целого
= 0 для любого целого  .
.
Доказательство (ДОК 21) Здесь по обобщённой интегральной формуле Коши при любом n получается, что 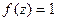 . Затем любая производная от константы есть 0. Поэтому результат всегда 0.
. Затем любая производная от константы есть 0. Поэтому результат всегда 0.
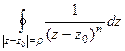 = 0 для
= 0 для 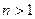 .
.
Особые точки и вычеты
Нули аналитической функции.
Определение. Точка 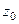 называется нулём функции
называется нулём функции 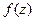 , если
, если 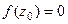 .
.
Мы сначала изучим нули функции, для того, чтобы затем изучить более подробно типы точек разрыва. Если 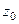 является нулём для
является нулём для 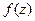 то в этой же точке предел
то в этой же точке предел  равен
равен 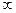 .
.
Вспомним, что в 1 семестре было ещё название «бесконечно-малая» и «бесконечно-большая» функция в точке. Бесконечно-малые могли быть разных порядков. Есть и здесь аналогичное более подробное определение, различающее порядки бесконечно малых:
Определение. Точка 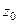 называется нулём порядка m функции
называется нулём порядка m функции 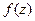 , если
, если 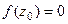 и функция представима в виде
и функция представима в виде 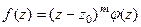 , где
, где 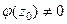 .
.
Определение. Точка 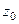 называется правильной точкой функции
называется правильной точкой функции 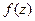 , если
, если 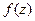 является аналитической в
является аналитической в 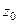 , и особой точкой, если она не является аналитической в
, и особой точкой, если она не является аналитической в 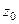 .
.
Определение. Точка 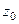 называется изолированной особой точкой, если в некоторой её окрестности
называется изолированной особой точкой, если в некоторой её окрестности 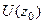 нет других особых точек.
нет других особых точек.
Существует такая классификация особых точек в зависимости от предела 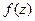 .
.
| Название | Устранимая особая точка | Полюс | Существенно-особая точка |
| При каком условии | 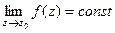
| 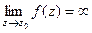
| 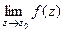 не существует
не существует
|
Пример
(  ) )
|  = = 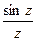
|  = = 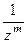
| 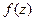 = = 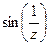
|
Лемма. Точка 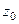 является нулём функции
является нулём функции 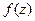
 она является полюсом функции
она является полюсом функции  .
.
Док-во очевидно: 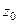 является нулём функции
является нулём функции 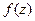
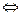 функция
функция 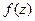 представима в виде
представима в виде 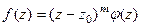 , причём
, причём
 . Это эквивалентно тому, что
. Это эквивалентно тому, что 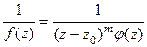 =
=
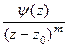 , где
, где 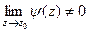 , а предел знаменателя равен 0. Это означает, что
, а предел знаменателя равен 0. Это означает, что 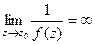 .
.
В связи с этим, естественным образом возникает определение полюса порядка 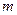 : точка
: точка 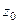 называется полюсом порядка m для функции
называется полюсом порядка m для функции 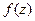 , если для функции
, если для функции  она является нулём порядка m.
она является нулём порядка m.
Замечание. Нуль и полюс функции соответствуют понятиям «бесконечно малая» и «бесконечно большая» функция в точке (из 1 семестра).
Пример. Указать тип всех особых точек для функции:
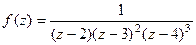 .
.
Решение. В знаментателе нули 1-го, 2-го и 3-го порядка, а именно, точки 2,3 и 4. Тогда для 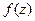 :
:  полюс 1-го порядка,
полюс 1-го порядка,
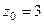 полюс 2-го порядка,
полюс 2-го порядка, 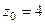 полюс 3-го порядка.
полюс 3-го порядка.
Теорема. Если 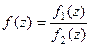 , причём точка
, причём точка 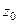 является нулём порядка m для функции
является нулём порядка m для функции 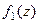 , и нулём порядка n для функции
, и нулём порядка n для функции 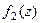 , то при
, то при 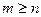 точка
точка 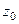 устранимая или правильная точка, а при
устранимая или правильная точка, а при 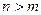 полюс порядка
полюс порядка  для функции
для функции  .
.
Доказательство (ДОК 22). Если 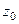 - нуль порядка m и n соответственно для числителя и знаменателя, то
- нуль порядка m и n соответственно для числителя и знаменателя, то 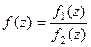 =
= 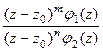 =
= 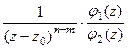 где
где  для каждой из двух функций. Тогда можно обозначить
для каждой из двух функций. Тогда можно обозначить  и в итоге
и в итоге 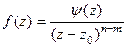 , это и означает, что полюс порядка
, это и означает, что полюс порядка 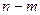 .
.
Пример. Определить тип особой точки  для функции
для функции 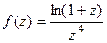 .
.
Решение. Представим функцию в числителе в виде разложения в ряд Тейлора.
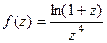 =
= 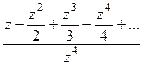 =
= 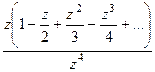 в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка
в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка  полюс 3 порядка.
полюс 3 порядка.
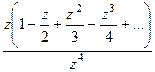 =
= 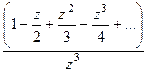 =
= 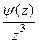 . В числителе после сокращения осталась функция, имеющая ненулевой предел.
. В числителе после сокращения осталась функция, имеющая ненулевой предел.
Дата: 2019-11-01, просмотров: 294.