Действия с комплексными числами.
Вспомнить из основных действий с комплексными числами:
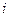мнимая единица. 
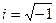. Комплексное число 
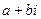, где 
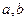- действительная и мнимая части Re(z), Im(z).
Замечание. В 4-мерном пространстве существует система кватернионов, обобщающая клмплексные числа, они строятся похожим образом: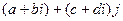 
, затем 
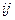обозначается 
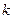, и получаем 
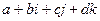. Обобщение в 3-мерном пространстве невозможно, т.к. в таком случае всегда получится система с делителями нуля, то есть 
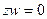, где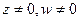 
.
Сопряжённое число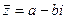 
, если 
.
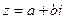При этом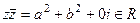 
.
Выражение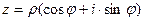 
называется тригонометрической формой комплексного числа, 
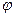- его аргументом, 
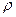- модулем.
.
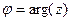
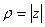Это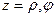 
такие же, как в полярных координатах.
Умножение и деление в тригонометрической форме.
= 
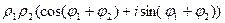
(умножить их модули и сложить аргументы).
Формула деления двух комплексных чисел в тригонометрической форме: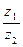 
= 
.
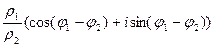Формула Муавра для возведения в степень:
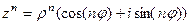
Корень порядка n вычисляется по такой формуле:
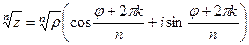
Между прочим, действительную и мнимую часть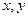 
для числа 
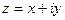можно выразить через 
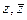. Докажем такие формулы:
, 
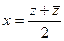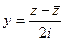
Доказательство (ДОК 5).
Сложим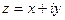 
и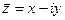 
.
= 
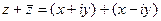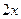, тогда .
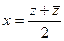Вычтем 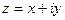и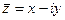 
.
= 
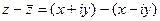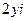, тогда 
.
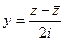Формула Эйлера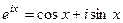 
.
Доказательство (ДОК 6).
Обобщение любой функции на случай комплексного переменного можно проводить с помощью рядов. Поскольку существует любая степень мнимой единицы 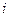, например 
, 
, 
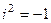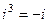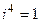, и т.д. то этот подход возможен. Вспомним разложение экспоненты по формуле Тейлора.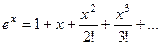 
Тогда вычислим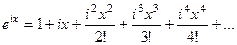 
=
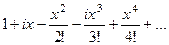теперь соберём в отдельные слагаемые все части, где нет 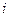, и где есть .
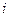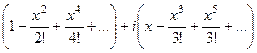но ведь в 1 и 2 скобках стоят разложения 
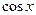и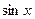 
. Итак, 
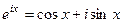, что и требовалось доказать.
Теперь для любого числа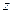 
можно вычислить 
:
= 
= 
= 
= 
.
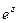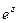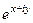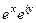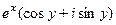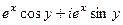Для сопряжённого числа можно вычислить аналогично:
= 
= 
= 
= 
.
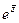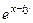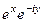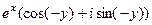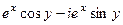(здесь воспользовались чётностью cos и нечётностью sin).
Получается, сопряжение под знаком экспоненты приводит
Функции комплексного переменного.
Только что мы рассмотрели функцию =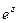 
.
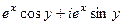Обобщим на комплексную плоскость синус и косинус.
Верны такие формулы: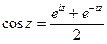 
, 
.
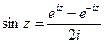Доказательство (ДОК 7).
Рассмотрим для действительного числа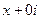 
и покажем, что данные функции, а именно 
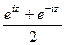и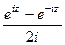 
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
1) 
= 
= 
= 
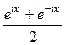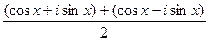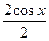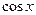
2) 
= 
= 
= 
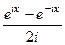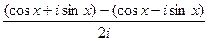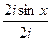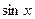
Неограниченность синуса и косинуса в комплексной плоскости.
Пример.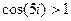 
.
Вычислим: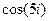 
= 
= 
.
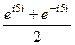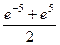
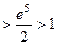Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
.
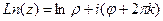Доказательство (ДОК 8).
,
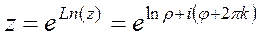
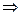
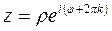
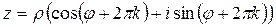это означает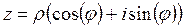 
так как синус и косинус не зависят от прибавления угла, кратного 
. Это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа.
Если вычислять логарифм положительного действительного числа, то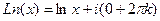 
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 
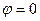. Для любого числа, которое не является действительным положительным, 
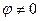, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае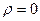 
, и не существует 
.
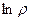Пример. Вычислить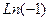 
.
Здесь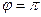 
, 
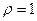. Поэтому 
= 
.
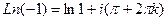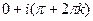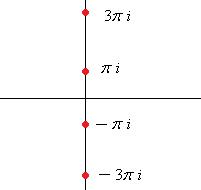
Точки в комплексной плоскости: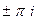 
, 
, 
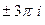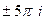, и так далее.
Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
ЛЕКЦИЯ 3. 16.09.2019
Для всякой функции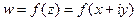 
можно отдельно выделить действительную и мнимую части, и представить в виде
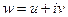. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 
, 
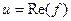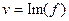. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 
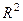в 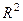, а именно 
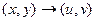. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
Пример. Разложить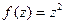 
на действительную и мнимую часть, изобразить искажения плоскости при переходе 
.
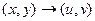1) 
= 
= 
= 
.
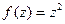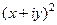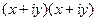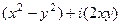Таким образом,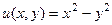 
, 
.
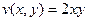Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем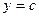 
, при этом 
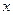изменяется от 
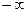до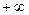 
, пусть движение задано с помощью параметра 
:
.
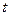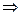
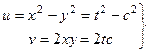Чтобы составить уравнение, взаимосвязывающее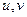 
, и узнать, какая это кривая, исключим параметр 
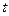, выразив из второго уравнения: 
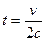, тогда 
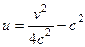. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 
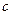, тем левее вершина, и тем более пологая парабола получается, ведь 
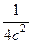при этом меньше. А если 
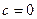, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 
.
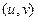Аналогично, для какой-либо вертикальной прямой:
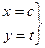
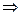
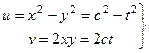. Тогда, исключая параметр 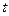, получим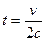 
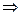
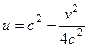. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении 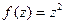, а красным - вертикальные прямые и их образы:
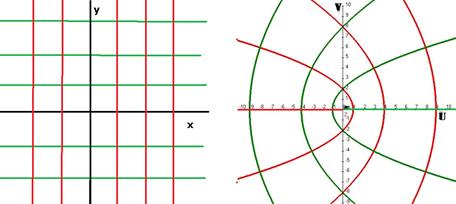
Пример. Разложить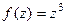 
на действительную и мнимую часть.
Используем то, что нашли ранее: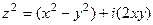 
, тогда
= 
= 
.
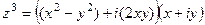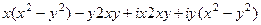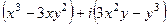Здесь 
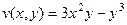
Пример. Разложить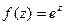 
на действительную и мнимую часть.
По формуле Эйлера: =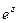 
= 
= 
= 
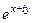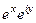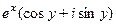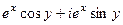, тогда 
, 
.
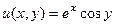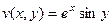Изучим деформации плоскости при действии линейной функции вида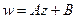 
, где коэффициенты 
, 
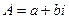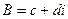это тоже некоторые комплексные числа. При этом очевидно, что 
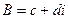приводит к сдвигу плоскости на вектор 
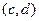, поэтому сначала более подробно изучим именно 
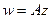без сдвига.
= 
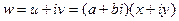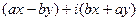. Но такое отображение можно представить с помощью линейного оператора:
= 
.
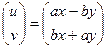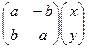Введём величину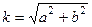 
, тогда существует какой-то угол 
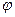, для которого 
, 
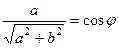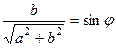. Причём заметим, что это именно 
, 
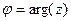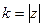для исходного комплексного числа.
Тогда матрица линейного оператора имеет вид: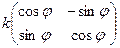 
то есть это композиция растяжения и поворота плоскости, причём поворот на угол 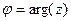, а растяжение или сжатие на 
.
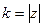(ДОК 9). Доказать что линейное отображение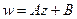 
в комплексной плоскости есть композиция растяжения, поворота и сдвига.
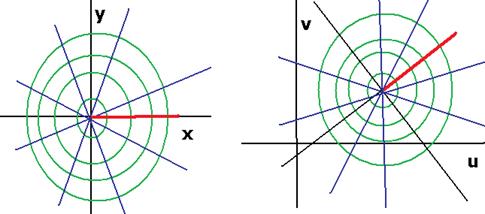
На этом чертеже показано, как изменяется плоскость при линейном отображении. Красным веделено горизонтальное направление, после отображения оно повёрнуто.
Замечание. Отображение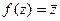 
соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.
Дата: 2019-11-01, просмотров: 233.
