1. M[X]=np
2. D[X]=npq
3. 
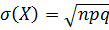
4. 
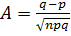
5. 
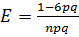
6. 
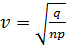
7. 
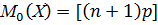
Примеры:
Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в цель.
Решение:
Поскольку p=0,7 , то q=1-p=1-0,7=0,3. По условию n=5, k=2, тогда по формуле находим:
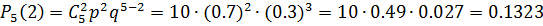
Ответ: вероятность равна 0.1323
Доля изделий из хлопка на предприятии составляет 30%. Чему равно наивероятнейшее число изделий из хлопка в случайно отобранной партии из 75 изделий.
Решение:
По условию n=75, p=0.3, поэтому q=1-p=0,7 . Поэтому:
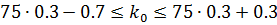т.е 
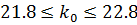
Из последнего неравенства следует, что k0=22 (k0=[22.8])
Ответ: наивероятнейшее число равно 22.
Геометрическое распределение
Проведем независимые испытания, в каждом из которых вероятность того, что событие произойдет, равна p (0< p<1), и, соответственно, вероятность того, что не произойдет, равна q (q=1- p ) . И поставим условие, что, как только событие произойдет, мы заканчиваем испытания. Т.е, если событие произошло в k-ом испытании, то в предшествующих k-1 испытаниях оно не произошло. Введем дискретную случайную величину Х – число испытаний, которые нужно провести до первого совершения события. Очевидно, возможными значениями X являются натуральные числа: x1=1, x2=2, … .
Пусть в первых k-1 испытаниях событие не произошло, а в k-ом испытании произошло. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий, найдем по формуле:
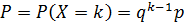
Геометрическим распределением называется распределение дискретной случайной величины X, определяемое формулой:
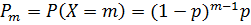, где 0 < p < 1; m=1, 2, …
Примерами реальных случайных величин, распределенных по геометрическому закону, являются: число выстрелов до первого попадания в цель, число испытаний до первого положительного результата, число бросаний кубика до первого выпадения нужной цифры и т.д.
Ряд распределения случайной величины X , имеющей геометрическое распределение, имеет вид:
| xi | 1 | 2 | 3 | … | m |
| pi | p | qp | q2p | … | qm-1p |
Характеристики геометрического распределения
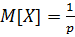
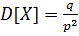
3. 
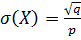
4. 
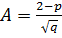
5. 
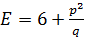
6. 
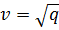
7. 
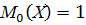
Пример:
Вероятность поражения цели равна 0,6. Стрельба по мишени происходит до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.
Решение:
Случайная величина X - число сделанных выстрелов - имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:
| xi | 1 | 2 | 3 | … | m | … |
| pi | 0.6 | 0.24 | 0.096 | … | 0.6∙0.4m | … |
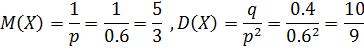
Вероятность того, что для поражения цели потребуется не более трёх патронов: P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3) = 0.6+0.24+0.096 = 0.936.
Ответ: вероятность равна 0.936
Распределение Пуассона
Рассмотрим случай, когда число n независимых испытаний является достаточно большим, а вероятность того, что событие произойдет в каждом из этих испытаний p - достаточно малым.
Положим np=a, где a постоянная величина. Это значит, что среднее число совершения события в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.
Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой:
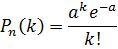
постоянную a = np называют параметром распределения Пуассона.
Закон Пуассона зависит от одного параметра a. Он является одновременно математическим ожиданием и дисперсией случайной величины X , распределенной по закону Пуассона.
Дата: 2019-11-01, просмотров: 156.
