Распределение Бернулли
Проведем n независимых испытаний, в каждом из которых событие может произойти или не произойти. Все испытания имеют одинаковые условия и вероятность того, что событие произойдет в каждом испытании одна и та же. Обозначим эту вероятность через p, а вероятность не совершения события через q (q=1-p).
Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p и q ≡1- p соответственно. Таким образом: P ( X =1)= p , P ( X =0)= q .
Говорят, что событие {X=1} является «успехом», а событие {X=0} — «неудачей». Эти названия условны, и могут быть изменены, в зависимости от условий.
Вероятность того, что в серии из n независимых испытаний событие произойдет ровно k раз (и не произойдет n-k раз) обозначим через Pn(k ), тогда 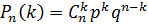 , где
, где 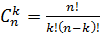 . Данную формулу называют формулой Бернулли.
. Данную формулу называют формулой Бернулли.
Число k0, которому при указанном n соответствует максимальная биноминальная вероятность Pn(k0), называется наивероятнейшим числом появления события А.
При заданных значениях n и p число определяется неравенствами:
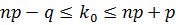
Следствие :
1. Если число 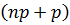 – целое, то
– целое, то 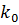 имеет два значения:
имеет два значения:
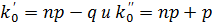 .
.
2. Если число 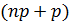 не является целым, то
не является целым, то 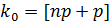 - целая часть числа (np+p).
- целая часть числа (np+p).
Характеристики распределения Бернулли
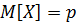
2. D[X]=pq
3. 
4. 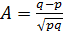
5. 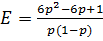
6. 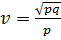
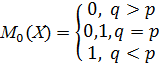
Примеры:
В тире Иван совершает 7 выстрелов по тарелкам с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания? б) не менее 5 попаданий?
Решение:
а) совершили n=7 независимых друг от друга испытаний с вероятностью попадания в тарелку в каждом из них p=0.8 . Вероятность того, что будет точно m=4 попаданий вычисляем по формуле Бернулли:
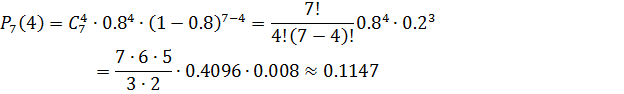
Ответ: вероятность равна 0.1147.
б) событие А, смысл которого в том, что при n=7 выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий: B – 5 попаданий из 7, событие C – 6 попаданий с 7 и D – все 7 выстрелов метки.
По формуле Бернулли находим вероятности событий:
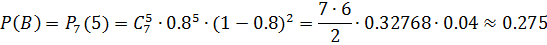
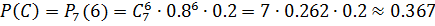
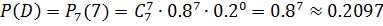
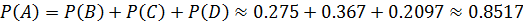
Ответ: вероятность равна 0.8517.
Биноминальное распределение
Представим, что в одинаковых условиях мы проводим n независимых испытаний, в каждом из которых событие может произойти с вероятностью p или не произойти с вероятностью q ( q =1- p ). В каждой серии из n испытаний событие может либо не произойти, либо произойти 1 раз, 2 раза, … , n раз. Рассмотрим дискретную случайную величину X, где Х - «число произошедших событий при n испытаниях». Найдем закон распределения этой случайной величины. Величина X может принимать следующие значения: x0= 0 , x1=1 , x2=2 , …, xn=n.
Вероятность pk того, что случайная величина X принимает значение xk , вычисляется по формуле Бернулли:
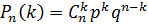 (k=0,1,2,…,n).
(k=0,1,2,…,n).
Закон распределения данной величины, определяемый формулой Бернулли, называется биноминальным.
Постоянные n и p, и входящие в формулу Бернулли, называются параметрами биноминального распределения.
Биноминальный закон распределения дискретной случайной величины X можно представить в виде следующей таблицы:
| xi | 0 | 1 | … | k | … | n |
| pi | qn | 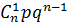
| … | 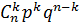
| … | pn |
Данная таблица строится следующим образом:
a) при x=0 , 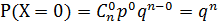 - это означает, что в n испытаниях событие А не произойдет ни разу,
- это означает, что в n испытаниях событие А не произойдет ни разу,
b) при x=1, 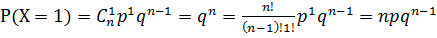 - вероятность того, что событие А произойдет один раз,
- вероятность того, что событие А произойдет один раз,
и т.д.,
c) при x=n, 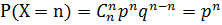 .
.
Дата: 2019-11-01, просмотров: 281.