Глава 1. Дискретная случайная величина

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

КУРСОВАЯ РАБОТА

Выполнила:

студентка 3 курса очной формы обучения

Герасимова Татьяна Александровна

Руководитель:

дфмн, проф. Хэкало С.П.

Итоговая оценка - ______________

Подпись______________________

Коломна – 2017

Содержание Введение………………………………………………………………........3. Глава 1. Дискретная случайная величина §1. Понятие дискретной случайной величины......................4. §2. Характеристики. Примеры..........….……………..……...4. Глава 2. Распределения дискретных случайных величин §1. Распределение Бернулли……………..……………..….10. §2. Биноминальное распределение…………......................12. §3. Геометрическое распределение ……………………….14. §4. Распределение Пуассона ………………….…………...16. Заключение………………………………………………………..............19. Список используемой литературы……………..……………………..…20.

Введение

Теория вероятностей — раздел математики, изучающий случайные события, величины, их свойства и операции над ними.

Становление теории вероятностей как науки относят к средним векам и связывают с первыми попыткам математического анализа азартных игр. Сегодня же теория вероятности плотно вошла в нашу жизнь и методы теории вероятностей можно встретить практически в любой дисциплине. Законы распределения случайных величин применяют не только к математике, физике, химии, но и к дисциплинам, носящим отчасти прогностический характер, таким как социология, экономика, политология и другие. Да и сам человек зачастую надеется на волю случая и удачу, это ли не есть теория вероятности.

Случайные величины подразделяются на дискретные и непрерывные величины.

Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси.

Примерами данной величины являются: температура комнаты в фиксированное время суток, масса наугад выбранного апельсина, рост наугад выбранного человека в толпе и т.д.

В данной работе мы рассмотрим понятие дискретной случайной величины, ее характеристики и законы распределения.

Глава 1. Дискретная случайная величина

Понятие дискретной случайной величины

Случайная величина ξ называется дискретной, если она принимает конечное или счетное множество значений. Такая случайную величину характеризуют таблицей, которая называется таблицей распределения:

ξ	a₁	a₂	…	a_n	…
P	р ₁	р ₂	…	р _n	…

где a₁, a₂, ..., a_n, ... – значения случайной величины ξ, а p₁, p₂, …, p_n, ... – вероятности этих значений, т. е. .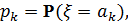

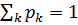Примеры: число попаданий в цель при n выстрелах; число выпавших решек, при подкидывании монеты; число вызовов, поступивших в скорую и др.

Характеристики

1) Математическое ожидание

Математическим ожиданием дискретной случайной величины X, принимающей:

a) конечное множество значений с законом распределения

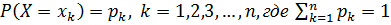называется сумма произведений ее значений на их соответствующие вероятности и записывается:

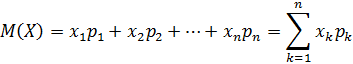
b) бесконечную последовательность значений с законом распределения 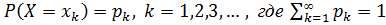также называется сумма произведений ее значений на их соответствующие вероятности и записывается:

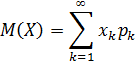
но, при условии, что этот ряд сходится абсолютно.

Замечание: математическое ожидание дискретной случайной величины приближенно равно среднему арифметическому всех ее возможных значений. Именно из-за этого, математическое ожидание M (X) дискретной случайной величины часто называют ее средним значением. Так как P₁+P₂+…+P_n=1, то

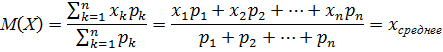
Распределение Бернулли

Проведем n независимых испытаний, в каждом из которых событие может произойти или не произойти. Все испытания имеют одинаковые условия и вероятность того, что событие произойдет в каждом испытании одна и та же. Обозначим эту вероятность через p, а вероятность не совершения события через q (q=1-p).

Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p и q ≡1- p соответственно. Таким образом: P ( X =1)= p , P ( X =0)= q .

Говорят, что событие {X=1} является «успехом», а событие {X=0} — «неудачей». Эти названия условны, и могут быть изменены, в зависимости от условий.

Вероятность того, что в серии из n независимых испытаний событие произойдет ровно k раз (и не произойдет n-k раз) обозначим через P_n(k ), тогда 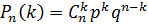, где 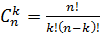. Данную формулу называют формулой Бернулли.

Число k₀, которому при указанном n соответствует максимальная биноминальная вероятность P_n(k₀), называется наивероятнейшим числом появления события А.

При заданных значениях n и p число определяется неравенствами:

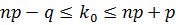
Следствие :

1. Если число 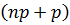– целое, то 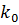имеет два значения:

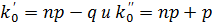2. Если число 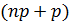не является целым, то 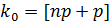- целая часть числа (np+p).

Биноминальное распределение

Представим, что в одинаковых условиях мы проводим n независимых испытаний, в каждом из которых событие может произойти с вероятностью p или не произойти с вероятностью q ( q =1- p ). В каждой серии из n испытаний событие может либо не произойти, либо произойти 1 раз, 2 раза, … , n раз. Рассмотрим дискретную случайную величину X, где Х - «число произошедших событий при n испытаниях». Найдем закон распределения этой случайной величины. Величина X может принимать следующие значения: x₀= 0 , x₁=1 , x₂=2 , …, x_n=n.

Вероятность p_k того, что случайная величина X принимает значение x_k , вычисляется по формуле Бернулли:

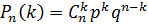(k=0,1,2,…,n).

Закон распределения данной величины, определяемый формулой Бернулли, называется биноминальным.

Постоянные n и p, и входящие в формулу Бернулли, называются параметрами биноминального распределения.

Биноминальный закон распределения дискретной случайной величины X можно представить в виде следующей таблицы:

x_i	0	1	…	k	…	n
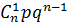
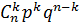
p_i	qⁿ		…		…	pⁿ

Данная таблица строится следующим образом:

a) при x=0 , 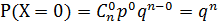- это означает, что в n испытаниях событие А не произойдет ни разу,

b) при x=1, 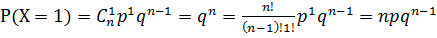- вероятность того, что событие А произойдет один раз,

и т.д.,

c) при x=n, .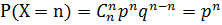

Распределение Пуассона

Рассмотрим случай, когда число n независимых испытаний является достаточно большим, а вероятность того, что событие произойдет в каждом из этих испытаний p - достаточно малым.

Положим np=a, где a постоянная величина. Это значит, что среднее число совершения события в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.

Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой:

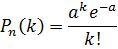
постоянную a = np называют параметром распределения Пуассона.

Закон Пуассона зависит от одного параметра a. Он является одновременно математическим ожиданием и дисперсией случайной величины X , распределенной по закону Пуассона.

Заключение

Моя тема является очень актуальной и востребованной во многих сферах жизни. Изучив огромное количество информации, я постаралась изложить основные аспекты данной темы, и пришла к выводу, что и сама часто использую дискретные случайные величины. Также я рассмотрела некоторые распределения данных величин и если изначально это были просто формулы, то теперь я понимаю, что законы распределения активно используются в прогнозировании. Сами мы не можем угадать каждое событие, которое произойдет, но, зная законы распределения, можем рассчитать, какое событие произойдет наиболее вероятно.

Существует большое количество распределений: нормальное, Пуассона, вырожденное, гипергеометрическое, биноминальное и т.д. Каждое из них было разработано для анализа данных, имеющих то или иное происхождение и обладающих некоторыми характеристиками.

Изучение мной данной темы, как будущего учителя математики полезно и тем, что эта информация пригодится для навыка обработки и анализа экспериментальных данных, анкет и тестов, которые широко используются в практической деятельности в школе.

Подводя итог своей курсовой работы, хочу сказать, что мне понравилось работать в данном формате. Это был полезный опыт.

Список используемой литературы

1. Дискретная случайная величина. [Электронный ресурс] URL: https://ru.wikipedia.org/wiki/ Дискретная_случайная_величина

2. Теория вероятностей: учебное пособие / Е.Н. Рассоха, Р24 Л.М. Анциферова, И.В. Березина. Оренбургский гос. ун-т.– Оренбург: ОГУ, 2011. - 243с

3. Законы распределения дискретных случайных величин. [Электронный ресурс] URL: http://komane.ru/nuda/soderjanie-1-binomialenoe-raspredelenie/main.html

4. Наиболее распространенные законы распространения дискретных случайных величин. [Электронный ресурс] URL: http://poznayka.org/s50253t1.html

5. М.В.Дубатовская Теория вероятностей и математическая статистика. Лекция 9. Основные законы распределения случайных величин. [Электронный ресурс] URL: http://economy.bsu.by/wp-content/uploads/2016/03/Lecture-9.pdf

6. Гусева Е.Н. Теория вероятностей и математическая статистика : [электронный ресурс] учеб. пособие / Е. Н. Гусева. – 5-е изд., стереотип. – М.: ФЛИНТА, 2011. – 220 с.

7. Теория вероятностей и математическая статистика: учебное пособие / К.А. Джафаров. – Новосибирск: Изд-во НГТУ, 2015. – 167 с.