1. Математическое ожидание постоянной величины равно этой постоянной: M (C)=C , где С=соnst.
Доказательство: константу C можно рассматривать как дискретную случайную величину, принимающую единственное значение с вероятностью 1, поэтому М(С)=С*1=С.
2. Постоянный множитель можно выносить за знак математического ожидания: M (CX )=CM ( X ) , С=соnst.
Доказательство: постоянную С можно рассматривать как случайную величину, причем С и X – независимые величины, поэтому:
М(СХ)=М(С)*М(Х)=С*М(Х).
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M (X+Y)=M(X)+M(Y).
Доказательство: 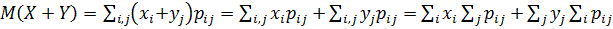
Т.к 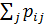 - представляет собой не что иное, как полную вероятность того, что величина Х примет значение х i . то
- представляет собой не что иное, как полную вероятность того, что величина Х примет значение х i . то 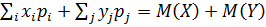 .
.
4. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий: M(X-Y)=M(X)-M(Y).
Доказательство: 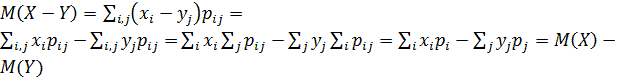 .
.
5. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин: 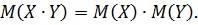
Доказательство: 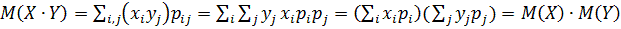
Пример:
Найти математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей:
| xi | 3 | 4 | 5 | 6 | 7 |
| pi | 0.1 | 0.2 | 0.5 | 0.2 | 0.1 |
Решение:
М(Х)=3*0.1+4*0.2+5*0.5+6*0.2+7*0.1=0.3+0.8+2.5+1.2+0.7=5.5
Неравенства выполняются: 3<5.5<7.
Ответ: математическое ожидание данной случайной величины равно 5.5.
2) Мода
Модой дискретной случайной величины называется ее значение, принимаемое, с наибольшей вероятностью по сравнению с двумя соседними значениями и обозначается через М0(Х).
Пример: Найти моду случайной величины Х, заданной следующим рядом распределения:
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0. 2 | 0. 4 | 0. 2 5 | 0. 1 | 0. 05 |
Решение: в силу определения М0(Х)=1.
3) Моменты случайных величин
Начальным моментом k-го порядка случайной величины Х, называется математическое ожидание k-ой степени этой величины:
vk(X)=M(Xk)
Для дискретной случайной величины Х начальный момент k-го порядка выражается суммой:
a) 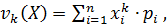 если она принимает конечное множество значений.
если она принимает конечное множество значений.
b) 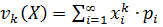 , если дискретная случайная величина принимает счетное множество значений и при условии, что этот ряд сходится абсолютно.
, если дискретная случайная величина принимает счетное множество значений и при условии, что этот ряд сходится абсолютно.
Центрированной случайной величиной называется отклонение случайной величины Х от ее математического ожидания, т.е 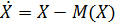 . Центрирование случайной величины равносильно переносу начала отсчета в точку mx =M (X).
. Центрирование случайной величины равносильно переносу начала отсчета в точку mx =M (X).
Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени центрированной случайной величины:
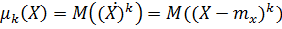
Центральный момент дискретной случайной величины Х выражается суммой:
a) 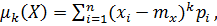 если она принимает конечное множество значений.
если она принимает конечное множество значений.
b) 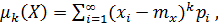 если дискретная случайная величина принимает счетное множество значений и при условии, что ряд сходится абсолютно.
если дискретная случайная величина принимает счетное множество значений и при условии, что ряд сходится абсолютно.
4) Дисперсия
Математическое ожидание квадрата соответствующей центральной величины называется дисперсией, или рассеянием:
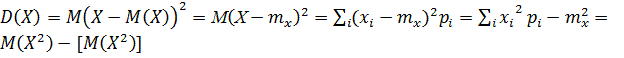
Свойства дисперсии
1. Дисперсия постоянной величины равна нулю.
Доказательство: воспользуемся 1 свойством математического ожидания, D(C)=M[C-M(C)]2=M(C-C)2=M(0)=0.
2. Постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат: D(CX)=C2D(X).
Доказательство: в силу 2 свойства математического ожидания имеем, что 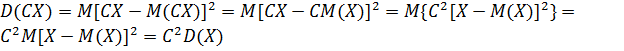 .
.
3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме дисперсий: 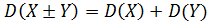 .
.
Доказательство: 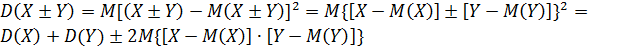 .
.
Величины X и Y независимы, поэтому величины X-M(X) и Y-M(Y) также независимы, следовательно: 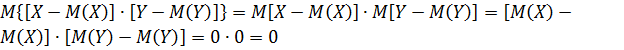 . Следовательно, D(X
. Следовательно, D(X 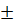 Y)=D(X)+D(Y).
Y)=D(X)+D(Y).
Пример:
| Х | 1 | 3 | 5 |
| р | 0.2 | 0.5 | 0.3 |
Найти дисперсию случайной величины, ряд распределения которой:
Решение:
М[X]=1×0.2+3×0.5+5×0.3=0.2+1.5+1.5=3.2. По определению,
D[X]=(1-3.2)2×0.2 + (3-3.2)2×0.5 + (5-3.2)2×0.3 = (-2.2)2×0.2 + (-0.2)2×0.5 + 1.82×0.3 = 4.84×0.2 + 0.04×0.5 + 3.24×0.3=1.96.
Ответ: дисперсия данной случайной величины равна 1.96.
5) Среднее квадратическое отклонение. Асимметрия и Эксцесс
В качестве характеристики рассеивания намного удобнее пользоваться числом, размерность которого совпадает с размерностью случайной величины, поэтому дисперсия не всегда удобна и из нее извлекают корень квадратный.
Средним квадратическим отклонением случайной величины X называется квадратный корень из ее дисперсии:
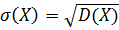
Коэффициентом вариации называют отношение среднего квадратического отклонения к математическому ожиданию:
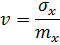
Коэффициент вариации применяется для неотрицательной случайной величины в качестве характеристики «степени ее случайности».
Коэффициентом асимметрии А случайной величины Х, называется величина:
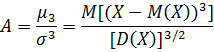
Коэффициентом эксцесса случайной величины Х, называется величина:
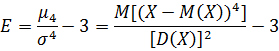
Дата: 2019-11-01, просмотров: 296.