1. Сколько и каких может быть пересечений для четырех множеств A, B, C, D?
2. Изобразить все возможные ситуации из п.1 в виде диаграммы Эйлера-Венна.
3. С помощью диаграмм Эйлера-Венна проверить равенства:
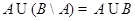
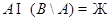
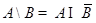
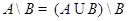
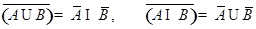(Законы де Моргана)
Замечание: чем больше Вы рассмотрите различных "взаимоположений" множеств 
и 
,
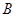Тем лучше.
Метод математической индукции
1. Доказать равенство
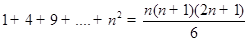
2. неравенство
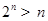
3. Доказать что-нибудь "геометрическое":
,
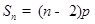где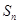 
- сумма внутренних углов выпуклого n-угольника.
Комбинаторика: Перестановки. Размещения. Сочетания. Треугольник Паскаля. Бином Ньютона.
1. Вычислить:
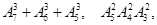
2. Проверить равенства:
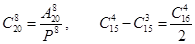
3. Решить уравнение: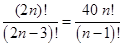 
4. Решить уравнение: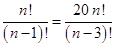 
3. Сколько трехцветных флагов можно составить из 7
базовых цветов крсн#оранж#желт#зелен#голуб#син#фиол
(Каждый Охотник Желает Знать Где Сидит Фазан), белого, черного и коричневого
(всего - 10 цветов):
а) без различия порядка их расположения?
б) с различием порядка их расположения?
4. Сколькими способами из 15 человек можно создать группы по 5 человек в каждой?
5. Сколько трехзначных чисел можно составить из цифр 1,2,3,4,5?
6. Сколькими способами из 14 человек, владеющих всеми четырьмя инструментами можно создать
ансамбль из гитариста, пианиста, скрипача и саксофониста?
Алгебраическая форма комплексного числа. Сложение, умножение и деление комплексных чисел. Комплексно сопряженные числа.
1. Вычислить (записать в алгебраической форме):
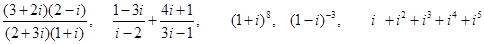
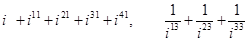
2. Решить уравнения:
3. Вычислить (записать в алгебраической форме), используя формулу для бинома Ньютона
(и треугольник Паскаля):
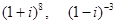
Связь декартовых и полярных координат на плоскости. Модуль и аргумент комплексного числа, тригонометрическая форма комплексного числа. Формула Эйлера и экспоненциальная форма комплексного числа
1. Записать комплексные числа в виде алгебраической формы,
изобразить их на комплексной плоскости:
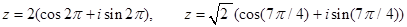
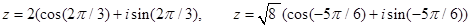
2. Записать комплексные числа в виде алгебраической формы. Указание: сначала привести к экспоненциальной форме, используя формулу Эйлера (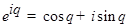 
)
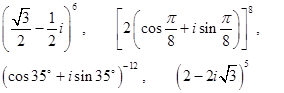
Найти алгебраическую форму с помощью формул Эйлера,
Изобразить число на комплексной плоскости.
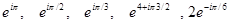
Экзамен
Теоретические вопросы к экзамену
1. Множества и операции над множествами. Основные числовые множества.
2. Алгебраическая форма комплексного числа. Сложение, умножение и деление комплексных чисел. Комплексно сопряженные числа.
3. Перестановки. Размещения. Сочетания. Треугольник Паскаля.
4. Бином Ньютона.
5. Вектор, координаты, сложение, умножение на число.
6. Сложение матриц. Умножение матриц.
7. Квадратная матрица, единичная матрица, матрица поворота на плоскости.
8. Определитель матрицы. Минор. Алгебраическое дополнение. Свойства определителя.
9. Обратная матрица. Алгоритм ее вычисления.
10. Системы алгебраических уравнений: случай однозначной разрешимости.
11. Системы алгебраических уравнений: случай неоднозначной разрешимости и случай несовместности.
12. Метод Гаусса для решения систем алгебраических уравнений.
13. Последовательность. Предел последовательности. Пример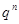 
. Теоремы о пределах.
14. Функция. Области определения и значений. Типы функций.
15. Графики и свойства основных элементарных функций.
16. Обратная функция. Примеры. Обратные тригонометрические функции.
17. Предел функции. Замечательные пределы.
18. Непрерывные функции. Непрерывность слева/справа. Точки разрыва 1-го и 2-го рода.
19. Производная функции. Геометрический смысл производной.
20. Основные правила дифференцирования. Таблица производных. Дифференцирование сложной функции.
21. Возрастание и убывание функции. Экстремумы функции и их нахождение.
22. Выпуклость функции. Точки перегиба.
23. Теоремы сложения и умножения вероятностей.
24. Классическая вероятность.
Дата: 2019-11-01, просмотров: 273.
