Основным источником возбуждения вынужденных колебаний мостовых сооружений на ВСМ является воздействие движущейся цепочки осевых сил, соответствующей схеме высокоскоростного поезда. При этом основным параметром, характеризующим динамическое воздействие подвижной нагрузки, выступает частота возбуждения, которая изменяется линейно в зависимости от скорости движения поезда. Когда частота возбуждения приближается к собственным частотам пролётного строения, могут возникать резонансные колебания.

Согласно данному выводу можно определить «критические» или резонансные скорости поезда, при которых будут наблюдаться указанные явления:

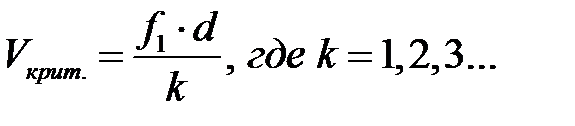
f₁ – первая собственная частота пролётного строения;

d – длина вагона, расчётного поезда.

Для демонстрации указанного явления приведены графики изменения вертикальных перемещений в середине пролёта балочного железобетонного пролётного строения, длиной 34,2 м при прохождении поезда ЭВС-1 «Сапсан» (длина вагона 25,26 м) с резонансной скоростью 108,2 м/с (389,5 км/ч) (рис. 14.11). Величина первой собственной частоты вертикальных изгибных колебаний составляет 4,283 Гц.

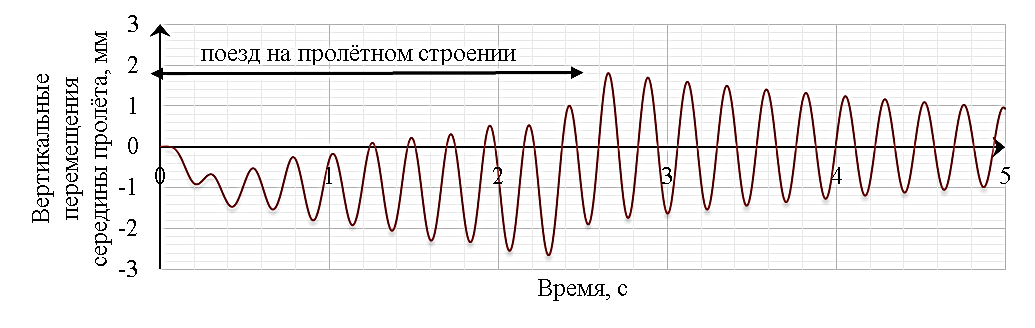
Рисунок 14.11. График изменения вертикальных перемещений в середине пролёта балочного железобетонного пролётного строения, длиной 34,2 м при прохождении поезда ЭВС-1 «Сапсан» с резонансной скоростью 108,2 м/с (389,5 км/ч)

Различие в величине динамического отклика пролётного строения можно увидеть из сравнения графиков изменения вертикальных перемещений в середине пролёта того же пролётного строения, длиной 34,2 м при прохождении поезда ЭВС-1 «Сапсан» со скоростью 95,94 м/с (345,4 км/ч) (рис. 14.12).

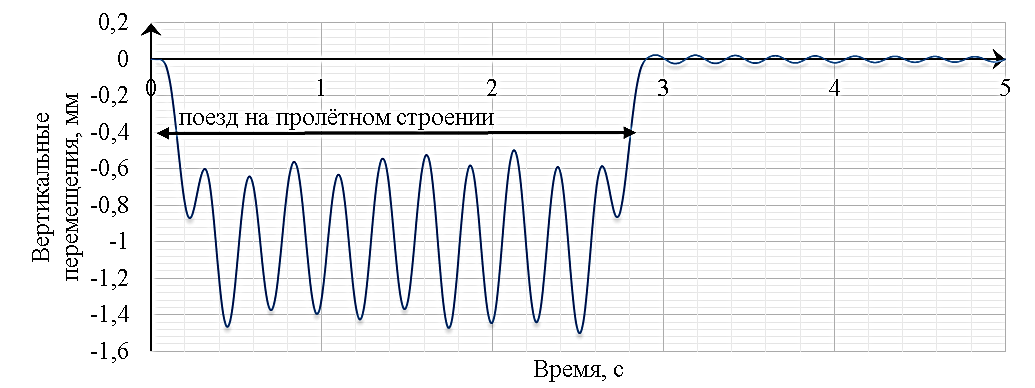
Рисунок 14.12. График изменения вертикальных перемещений в середине пролёта пролётного строения длиной 34,2 м при прохождении поезда ЭВС-1 «Сапсан»
со скоростью 95,94 м/с (345,4 км/ч)

Выше представлены два противоположных режима динамической работы пролётного строения при воздействии одного типа подвижного состава. В первом случае наблюдается основной резонансный режим колебаний пролётного строения (рис. 14.11), когда амплитуды вертикальных перемещений в середине пролёта нарастают в течение времени нахождения высокоскоростного поезда на пролётном строении. Во втором случае (рис. 14.12), скорость движения поезда соответствует режиму «антирезонанса», когда каждая последующая осевая сила в цепочке, за исключением последней, гасит колебания, вызванные предыдущей, и нарастания амплитуд колебаний не происходит. В итоге можно наблюдать колебания пролётного строения очень близкие к величине статических пульсаций при движении поезда с минимальной скоростью. Исходя из приведённых результатов любопытно отметить, что разница между рассмотренными скоростями движения поезда составляет всего 44,1 км/ч, в то время как реакция сооружения отличается весьма значительно.

В приведённых выше случаях рассмотрены характерные режимы, соответствующие резонансным и антирезонансным колебаниям пролётного строения при движении по нему высокоскоростного поезда. Для исследования более общего случая воздействия рассмотрен динамический отклик конструкции при воздействии поезда с нерезонансной скоростью. Ниже представлены графики изменения вертикальных перемещений (рис. 14.13) в середине пролёта пролётного строения длиной 34,2 м при движении поезда со скоростью 85,88 м/с (309,2 км/ч).

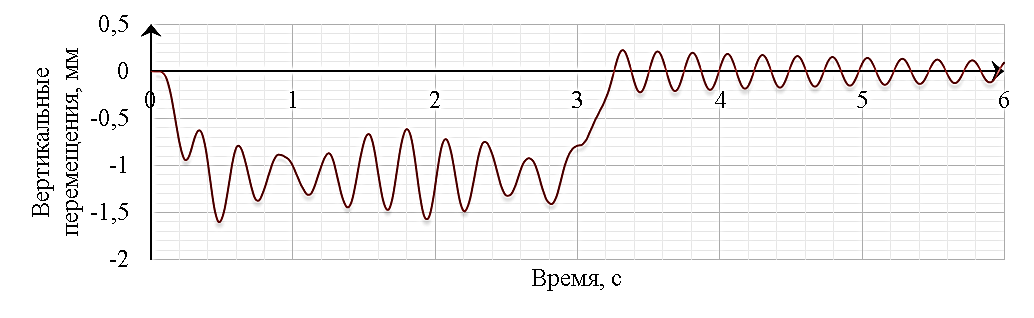
Рисунок 14.13. График изменения вертикальных перемещений в середине пролёта пролётного строения длиной 34,2 м при движении поезда со скоростью 85,88 м/с (309,2 км/ч).

При рассмотрении амплитудно-частотной характеристики колебаний пролётного строения для двух временных периодов, во время движения поезда по пролётному строению и после схода с него (рис. 14.14) видно, что пролётное строение совершает колебания с частотой, равной частоте вынужденных колебаний, вызванной движением поезда по сооружению
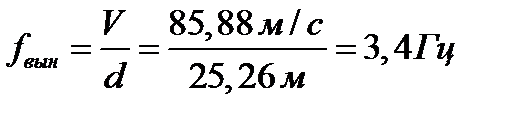( ) после схода поезда с пролёта, колебания становятся свободными, а их частота совпадает с первой собственной частотой вертикальных изгибных колебаний (4,283 Гц).

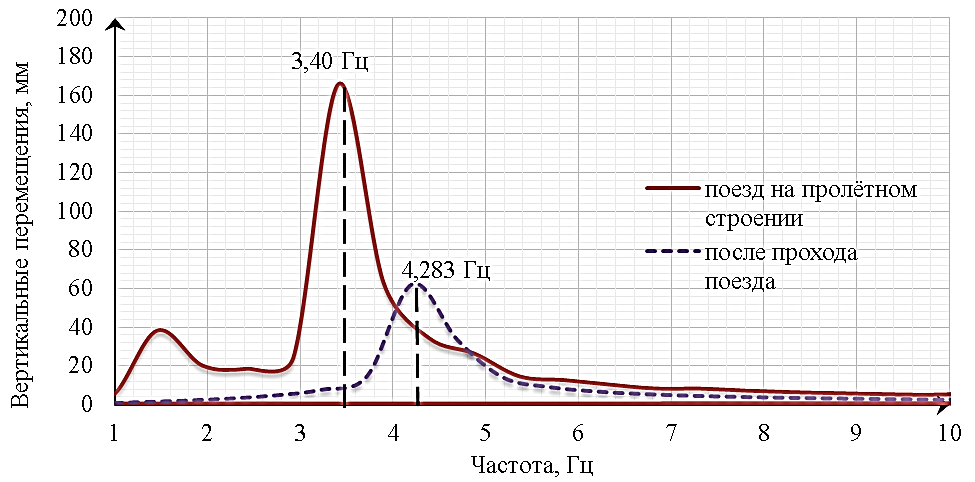
Рисунок 14.14. Амплитудно-частотная характеристика колебаний пролётного строения длиной 34,2 м при нахождении на сооружения и после прохода поезда