Управление предприятием в современных условиях должно базироваться на экономико-математических методах и моделях, в которых будут отображены основные закономерности его деятельности. Эти закономерности выражают объективные экономические связи в функционировании предприятия и должны учитываться при принятии решений относительно необходимого объема активов на предприятии, соотношением использования активов, себестоимостью и полученной прибылью.

Исследованию вопросов, связанных с использованием экономико-математичного моделирования в экономике, посвящено немало трудов как в мировой экономической литературе, так и в отечественной. Эти вопросы рассматривали Б. Райан, В. Хорн, Д. Мидлтон, Д. Стоун, К. Хитчинг, Ф. Бутинец, М. Пушкарь и другие.[ ]

Постоянное расширение сферы применения математического моделирования в экономике способствует созданию соответствующих программных систем. Если более ранняя экономическая регуляция рассматривалась часто как предмет политэкономии, то сейчас все более актуальным становится конструктивное внедрение методологии математического моделирования в сферу макроэкономики и микроэкономики. Таким образом, экономико-математическое моделирование несомненно остается актуальным направлением исследования процессов макро- и микроэкономического анализа и прогнозирования в современных условиях.

Для изучения разных экономических явлений экономисты используют их упрощенные формальные описания, которые называются экономико-математическими моделями. Экономико-математическая модель — математическое описание исследуемого экономического процесса. В экономико-математических моделях объектом является экономический процесс (например, использование ресурсов, распределение изделий между разными типами оборудования и тому подобное), а языком - классические или специально разработаны математические методы [5].

Эффективное управление предприятием в современных условиях должно базироваться на таких экономико-математических моделях, у которых будут отображены основные закономерности его деятельности. Эти закономерности должны выражать объективные экономические связи в функционировании предприятия и должны учитываться при принятии решений относительно необходимого объема активов на предприятии, соотношением использования как оборотных, так и необратимых активов, себестоимостью и прибылью. Таким образом, основной задачей, по нашему мнению, есть определение и достижение такого взаимного соответствия ресурсов (оборотных и необратимых активов), при котором обеспечивается достижение необходимого уровня прибыльности, достаточного для стойкого функционирования и развития предприятия, а также создания условий для расширения производства.

На основе логического анализа и системы группировок выявляется перечень признаков, который может быть положен в основу регрессивной модели связи. Если результативный признак находится в стохастической (вероятностной) зависимости от многих факторов, то уравнения, выражающие эту зависимость, называются многофакторными уравнениями регрессии.

Покажем взаимосвязь между снижением затрат на 1 изделие (X1), среднегодовым выпуском изделий (X2) и себестоимостью 1единицы изделия (Y). Для этого составим вспомогательную таблицу (Приложение ). Для математического выражения связи между выбранными факторами может быть использовано следующее уравнение:

,

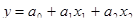Параметры a₀, a₁, a₂ определяют в результате решения системы 3-х нормальных уравнений:

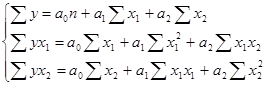
В результате решения данной системы (см. Приложение ) на основе исходных данных по 4 участкам было получено следующее уравнение регрессии:

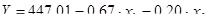
Коэффициент регрессии a₁ = -0,67 показывает, что при уменьшении затрат на 1 единицу изделия , себестоимость 1 единицы изделия снижается в среднем на 0,67 грн. (при условии постоянства среднегодового выпуска). Коэффициент a₂ = -0,20 свидетельствует о том, что при увеличении среднегодового выпуска изделий себестоимость 1 изделия в среднем уменьшается на 0,20 грн. (при постоянной величине затрат на 1 изделие).

Теснота связи между признаками, включёнными в модель, может быть определена при помощи коэффициентов множественной корреляции:

,

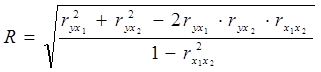где 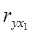, , 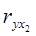 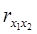- коэффициенты парной корреляции между x₁, x₂ и y. Формулы для нахождения данных коэффициентов можно представить следующим образом:

; ; ;

;              ;    ;

; ; ;

; ;   =

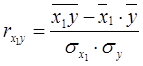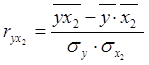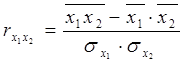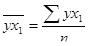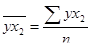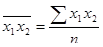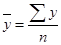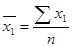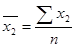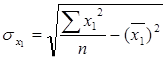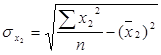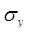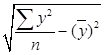
В рассматриваемом случае были получены следующие коэффициенты парной корреляции: 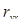= -0,37; 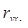= -0,59; 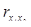= 0,56. Следовательно, между себестоимостью (y) и снижением затрат на 1 изделие(x₁) связь обратная средняя, между себестоимостью и среднегодовым выпуском изделий (x₂) связь обратная средняя. При этом связь между факторами прямая средняя ( 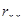= 0,56), нет мультиколлинеарности. Данное явление свидетельствует о вполне удачном выборе факторов.

Между всеми признаками связь средняя (R = 0,59). Коэффициент множественной детерминации (Д = R² * 100 = 34,81%) показывает, что 34,81% вариации себестоимости 1 изделия определяется влиянием факторов, включенных в модель.

Для оценки значимости полученного коэффициента R воспользуемся критерием Фишера, фактическое значение которого определяется по формуле:

,

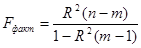 где n – число наблюдений,

m - число факторов.

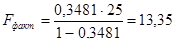
Для рассматриваемого случая получим F_факт = 13,35.

F_табл определяется при заданном уровне значимости (0,05) и числе степеней свободы: V₁ = n – m и V₂ = m – 1. Для нашего случая V₁=25, V₂=1, F_табл = 4,24.

Поскольку F_{факт >} F_табл, значение коэффициента R следует считать достоверным, а связь между x₁, x₂ и y - тесной.

Для оценки влияния отдельных факторов и резервов, которые в них заложены, также определяют коэффициенты эластичности, бета-коэффициенты, коэффициенты отдельного определения.

Коэффициенты эластичности показывают, на сколько % в среднем изменяется результативный признак при изменении факторного на 1% при фиксированном положении другого фактора:

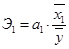 = -0,09 ;  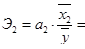            -0,28

Таким образом, изменение на 1% уменьшения затрат на 1 изделия ведёт к среднему снижению себестоимости на 0,09%, а увеличение на 1% среднегодового выпуска изделий - к среднему ее снижению на 0,28%.

При помощи β-коэфффициентов даётся оценка различия в степени варьирования вошедших в уравнение факторов. Они показывают, на какую часть своего среднего квадратического отклонения ( 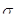) изменится результативный признак при изменении соответствующего факторного на величину своего среднего квадратического отклонения ( 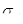). β-коэффициенты вычисляются следующим образом:

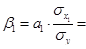 -0,10;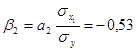

Это говорит о том, что наибольшее влияние на себестоимость 1 изделия с учётом вариации способен оказать второй фактор, т.к. ему соответствует наибольшая абсолютная величина коэффициента.

Коэффициенты отдельного определения используются для определения в суммарном влиянии факторов доли каждого из них:

;                       

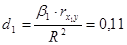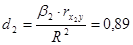
Таким образом, на долю влияния первого фактора приходится 11%, второго – 89%.