Критерии оценки структурной надежности радиотехнических систем методом статистического моделирования

Критерием оценки структурной надежности сетей связи методом статистического моделирования является вероятность наступления события - сеть связана.

На сегодняшний день в литературе известно несколько методов проверки сетей на связность: “поиск в глубину”, “разрастания” и “свертки”.

Известно, что метод “свертки” позволяет уменьшить до 50% (по сравнению с другими методами) затраты времени ЭВМ для данной процедуры. Суть данного метода заключается - одновременное соединение инцидентных вершин с произвольно выбранной вершиной до тех пор, пока сеть не представится в виде одной точки (если сеть связна) или множество точек (если сеть несвязна).

Однако методу, как и другим, присущ недостаток - резкое (нелинейное) увеличение затрат времени ЭВМ (по сравнению с другими методами) на процедуру проверки графа сети на связность.

Метод “разбиения". Суть метода “разбиения” состоит в следующем. Граф сети разбивается на подграфы, каждый из которых отдельно проверяется на связность методом “свертки". В результате получаем новый граф - суперграф, который в свою очередь проверяется на связность. Если суперграф связен, то делается вывод, что исходный граф сети связен. За счет “разбиения” исходного графа сети на подграфы появляется возможность работать на пологом участке кривой, отображающей зависимость затрат времени ЭВМ от размерности графа.

Оценка сложности метода “разбиения". Рассмотрим граф сети в виде квадратной решеткою Конечно, едва ли следует ожидать, что граф реальной сети будет иметь структуру с квадратной ячейкой. Однако оценки, полученные для данной ситуации, дадут представления о сложности предлагаемого метода проверки графа сети на связность. Вложим данный граф в прямоугольную систему координат.д.опустим, число вершин по осям x и y одинаково и равно L. Общее число вершин в графе будет равно S=L²

В данном случае по методу “свертки” достаточно выполнить

L-1=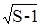

итераций для определения связности графа. Тогда сложность метода “свертка” будет определятся

Q=M ( ),

где M - степень каждой вершины графа.

Допустим, что граф разбит на n равных подграфов, тогда сложность

проверки каждого подграфа составит

G₁=M ( 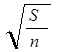-1)

Учитывая проверку на связность полученного суперграфа, размерность которого равна n, получим оценку сложности метода “разбиения"

Q_n=M ( 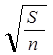-1) +M ( 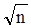-1).