Классификация структур радиотехнических систем

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Введение

Разработка современных информационных систем включает в качестве одного из обязательных этапов проектирования анализ их надежности. Проблема усложняется тем, что коммутационные сети, к анализу которых в конечном итоге сводится данная задача, являются сильно связными структурами (междугородние сети связи, системы управления и др.). Это затрудняет, а порой делает невозможным расчет их надежности строго аналитическими методами, как это имеет место, например, для параллельно-последовательных сетей. Единственным численным методом расчета надежности сильно связанных сетей остается метод полного перебора, который, однако, даже с привлечением быстродействующих ЭВМ, не позволяет анализировать сети, содержащие более 15-20 случайных компонент.

В тех случаях, когда в состав информационной системы включены не только физические объекты (каналы связи, транспортные средства, релейно-контактные элементы и т.п.), но и объекты, означающие такие понятия, как ”логическая связь", ”операция" и т.п. Одним из способов повышения надежности таких сетей является простое дублирование составляющих их элементов. Однако вследствие ограниченности ресурсов такой путь в большинстве случаев нерационален. К настоящему времени аналитический аппарат синтеза оптимальных структур коммуникационных сетей практически еще не разработан вследствие исключительной сложности в самой задаче. В инженерной практике при решении подобного рода задач часто прибегают к методу частичного перебора. Так, например, при выборе оптимальной структуры сети связи в качестве частных вариантов могут анализироваться некоторые типовые схемы соединения узловых пунктов. Применяется так называемый радиальный принцип соединения узлов, принцип связи ”каждого с каждым” или ”каждого с ближайшим", иерархический принцип соединения и т.д. Одним из основных критериев оценки этих вариантов является прежде всего надежность передачи сообщения в сети.

Среди методов вероятностного анализа коммуникационных сетей будем различать алгоритмические, являющиеся по существу программами для решения задач на ЭВМ, и методы аналого-вероятностного моделирования.

Одним из основных методов решения поставленных задач является метод статистического моделирования. Критерием оценки структурной надежности сетей связи по этому методу является вероятность наступления события - сеть связанна.

Метод разложения

Несколько менее трудоемким является метод, основанный на разложении структуры сети относительно какого-нибудь ее элемента (метод разложения Шеннона-Мура). Идея этого метода заключается в том, чтобы свести анализируемую структуру к последовательно-параллельным соединениям и тем самым избежать полного перебора состояний. Для примера рассмотрим сеть простейшей структуры в виде мостика (рис.2.1).

Рисунок 2.1 Метод разложения

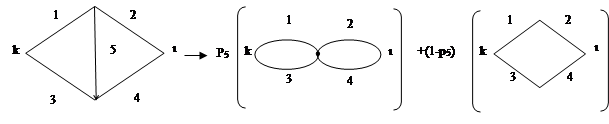Для простоты положим, что узлы этой сети идеально надежны, а ветви имеют конечную надежность р _i, i= 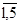. Нумерация ветвей приведена на рисунке. Проделаем с элементом под номером 5 ("перемычка" мостика) два опыта - "короткого замыкания", соответствующий исправному состоянию элемента, и "холостого хода", соответствующий его неисправному состоянию. Если перемычка находится в исправном состоянии, что случается с вероятностью p₅, то соединяемые ею узлы можно "стянуть" в смысле надежности (см. рис.2.1) и сеть будет иметь вид двух последовательно соединенных и параллельно включенных пар ветвей. Если перемычка находится в неработоспособном состоянии, что случается с вероятностью 1-p₅, то оставшаяся сеть будет иметь вид параллельного соединения цепочек.

Таким образом, мы "разложили" сеть относительно элемента 5, в результате чего получили две подсети с числом элементов на единицу меньше, чем в исходной сети. Поскольку обе подсети представляют собой последовательно-параллельные структуры, то, пользуясь формулами (2.3) и (2.4), можно сразу записать искомое выражение для вероятности связности сети относительно узлов r, l, используя для компактности обозначениеq_i=1-p_i.

H_rl=p₅ (1-q₁q₃) (1-q₂q₄) +q₅ [1- (1-q₁q₂) (1-q₃q₄)].

В более сложных структурах может потребоваться неоднократное применение теоремы разложения. Так, на рис.2.2 показано разложение относительно элемента 7 (верхняя строка), а затем по элементу 8 (нижняя строка). Получившиеся четыре подсети имеют последовательно-параллельные структуры и больше не требуют разложений. Легко видеть, что на каждом шаге число элементов в получающихся подсетях уменьшается на единицу а число подсетей, требующих дальнейшего рассмотрения удваивается. Поэтому описанный процесс в любом случае конечен, а число результирующих последовательно-параллельных структур составит 2^m, где т - число элементов, по которым пришлось провести разложение. Трудоемкость этого метода можно оценить величиной 2^m, что меньше трудоемкости полного перебора, но тем не менее все еще неприемлемо для расчета надежности реальных сетей коммутации.

Рисунок.2.2 Последовательное разложение сети

Расчет себестоимости

В данном проекте разработано программное обеспечение лабораторной работы на тему ” Исследование структурной надежности РТС". Ввиду отсутствия информации о подобных разработках осуществить сравнение данного продукта с аналогом не представляется возможным. Поэтому произведём расчёт себестоимости программы.

Себестоимость программного обеспечения можно определить по формуле 4.1:

С= (З / m) K ( t₁+t₂) (1+K_н) + 8 t₃ С_м, (4.1)

где С - себестоимость программного обеспечения;

З - среднемесячная заработная плата разработчика программы, (руб);

m - среднее количество рабочих дней в месяце;

К - коэффициент, учитывающий отчисления во внебюджетные фонды:

Пенсионный-28%.

Фонд занятости-1.5%

Фонд страхования-5.4%

Фонд мед. страхования-3.6%

Итого 38.5%, К=1.385

t₁ - время, затраченное разработчиком в днях:

1. Разработку требований к программе.

2. Составление алгоритма программы.

t₂ - время, затраченное на написание и отладку программы (дни),

K_{н. -}коэффициент, учитывающий накладные расходы. Мы его примем равным K_н.=2;

t₃ - время, затраченное на разработку программы с использованием машинного времени (дни).

Так как в данном случае время, на написание и отладку программы является временем, затраченным на разработку программы с использованием машинного времени, то t₂= t₃.

С_{м. -}стоимость одного часа машинного времени, (дни).

Среднемесячную заработную плату разработчика программы примем равную З=2000 рублей.

Количество рабочих дней в месяц примем равное m=20.

Коэффициент, учитывающий отчисления во внебюджетные фонды равен К=1.385.

Стоимость одного часа машинного времени примем равное С_м.=10 рублей.

Для расчета себестоимости необходимы затраты по времени. Для этого предлагается применять экспертные оценки. Работа по разработке программной продукции разбивается на этапы, для каждого этапа экспертами устанавливаются временные оценки. В качестве экспертов выступают автор проекта и руководитель дипломного проекта. На основании экспертных оценок затрат времени определяется средняя оценка, которая считается по формуле 4.2:

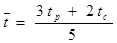, (4.2)

где t_p_-экспертная оценка руководителя, (дни);

t_c_-оценка автора проекта, (дни);

Оценка времени предусмотрена для трёх ситуаций:

1. Наименьшая возможная величина затрат.

2. Наиболее вероятная величина затрат.

3. Наиболее возможная величина затрат.

Экспертные оценки и средние оценки затрат времени приводятся в таблице 4.1:

Таблица 4.1 - Экспертные и средние оценки затрат времени

Этапы разработки программы	Наименьшая возможная величина зaтрат (дни)			Наиболее вероятная величина затрат (дни)			Наиболее возможная величина затрат (дни)
	t_p	t_c		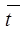t_p	t_c		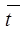t_p	t_c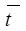
Подготовительное время, которое нужно потратить для того, чтобы приступить к написанию программы, t₁	6	5	5.6	7	6	6.6	9	8	8.6
Время, затраченное на написание и отладку программы, t₂=t₃	14	13	13.6	17	15	16.2	21	18	19.8

На следующем этапе рассчитывается ожидаемая величина затрат времени и стандартное отклонение этой величины для каждого этапа.

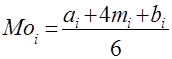, (4.3)

где Mo_i - ожидаемая величина затрат времени для каждого этапа времени, (дни);

а_i - средняя оценка наименьшей возможной величины затрат, (дни);

m_i - средняя оценка наиболее вероятной величины затрат, (дни);

b_i - средняя оценка наиболее возможной величины затрат, (дни);

G_i_-стандартное отклонение времени для каждого этапа, [дни].

Результаты ожидаемой величины и стандартное отклонения приводятся в таблице 4.2:

Таблица 4.2 - Результаты ожидаемой величины и стандартное отклонения.

Этапы разработки Программы	Средняя величина затрат времени по этапам			Ожидаемая величина затрат Времени для каждого этапа, Mo_i₍дни)	Стандартное отклонение времени для каждого этапа, G_i₍дни)
Этапы разработки Программы	наименьшей возможной, a_i₍дни)	наиболее вероятной, m_i ₍дни)	наиболее возможной, b_i₍дни)
Подготовительное время, которое нужно затратить для того, чтобы приступить к написанию программы, t₁	6	5.6	8.6	6.77	0.11
Время затраченное на написание программы и отладку, t₂= t₃	13.6	16.2	19.8	16.4	1.07

Зная математическое ожидание, по каждому этапу рассчитывается общая величина математического ожидания в целом по программе:

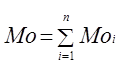(4.4)

Mo = 23.2 дня.

Зная стандартное отклонение, по каждому этапу рассчитывается общая величина стандартного отклонения в целом по программе:

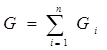, (4.5)

G = 1.18 дня.

В итоге себестоимость программы:

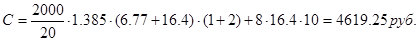
Данная программа предназначена для использования внутри ВУЗа.

Разработанная программа, позволяет проводить анализ различных типов структур сетей связи. Рассмотреть, как зависит надежность сети от выбранного типа структуры построения системы и от надежности линии связи, рассчитать надежность анализируемой системы, что практически не возможно реализовать в ручную.

Заключение

В данном проекте была разработана программа, которая позволяет рассчитывать структурную надежность радиотехнических систем методом статистического моделирования. Она значительно облегчает задачу расчета структурной надежности системы.

Используя данную программу, было проведено сравнения различных типов структур сетей. Наиболее надежными являются полносвязные структуры однако они требуют больших капитальных затрат. Наименьшие капитальные затраты требуются для построения иерархических структур, но они обладают плохой надежностью. Оптимальным соотношением между ценой и надежностью обладаю сотовые структуры.

Библиография

1. Бусленко Н.П. Моделирование сложных систем. М.: Наука, 1968.

2. Бойченко В.М., Гладкий В.С., Черный Е.И. Аналого-вероятностное моделирование систем из ненадежных элементов. - Изв. АН СССР, Техническая кибернетика, 1967, №1.

3. Гладкий В.С. Вероятностные вычислительные модели. М.: Наука, 1973.300с.

4. Гладкий В.С., Данилов А.Н. Новиков С.Н. Программа оценки структурной надежности сетей связи / Гос. ФАП СССР. - М., 1987.

5. Малиновский С.Т. Сети и системы передачи дискретной информации и АСУ / Учебник для электротехнических институтов связи. М.: Связь, 1979.384с.

6. Мизин И.А., Богатырев В.А., Кулешов А.П. Сети коммутации пакетов / Под ред.В.С. Семенихина. - М.: Радио и связь, - 408с

7. Толчан А.Я. О связности сети. Принципы построения сетей и систем управления. М.: Наука, 1964.

Приложение А

ПРОГРАМА.

uses crt;

Label 1;

Var

F1: text;

k1,n1,N,Ny, i,j,s,L,z,w,k,d: integer;

P: array [1. .50,1. .50] of real;

MS: array [1. .55,1. .55] of integer;

R: real;

m,h,mh: array [1. .66] of integer;

key: char;

PROCEDURE kol_node;

var r_key: char;

begin

repeat

window (1,1,80,25);

clrscr;

ASSIGN (F1,'FF1. txt');

rewrite (F1);

n1: =1;

write ('введите кол-во узлов s=');

readln (s);

r_key: =#27;

until r_key=#27;

close (f1);

end;

PROCEDURE kol_attemp;

var r1_key: char;

begin

window (1,1,80,25);

textbackground (blue);

clrscr;

repeat

write ('количество испытаний N=');

readln (N);

Ny: =0;

r1_key: =#27;

until r1_key=#27;

end;

PROCEDURE number_attemp;

label 1,2;

var param: byte;

d: integer;

begin

window (1,1,80,25);

textbackground (black);

clrscr;

assign (f1,'ff1. txt');

append (f1);

d: =0;

Ny: =0;

for i: =1 to s do

begin

m [i]: =0;

h [i]: =0;

mh [i]: =0;

for j: =1 to s do

begin

P [i,j]: =0;

MS [i,j]: =0;

end;

2: clrscr;

writeln ('Для автоматического ввода введите - 1');

writeln ('Для ручного ввода введите - 2');

readln (param);

if param=2 then

begin

n1: =1;

for i: =1 to s do

begin

n1: =n1+1;

for j: =n1 to s do

begin

write ('введите P [', i,',',j,'] =');

read (P [i,j]);

P [j, i]: =P [i,j] ;

end;

writeln;

END;

end;

if param=1 then

begin

n1: =1;

for i: =1 to s do

begin

n1: =n1+1;

for j: =n1 to s do

begin

P [i,j]: =random;

P [j, i]: =P [i,j] ;

end;

END;

end;

if (param<>1) and (param<>2) then goto 2;

for i: =1 to s do P [i, i]: =1;

for i: =1 to s do

begin

for j: =1 to s do

begin

write (' ',P [i,j]: 1: 3);

write (F1,' ',P [i,j]: 2: 3);

end;

writeln;

writeln (F1);

end;

1: while d<N do

begin

d: =d+1;

writeln (F1,'номер испытания N=',d);

R: =random;

writeln (F1,'R=',R: 1: 3);

for i: =1 to s do

begin

for j: =1 to s do

begin

if P [i,j] >R then MS [i,j]: =1

ELSE MS [i,j]: =0;

write (F1,' ',MS [i,j]);

end;

writeln (F1);

end;

k: =1;

k1: =0;

for j: =1 to s do

begin

mh [j]: =ms [1,j] ;

m [j]: =ms [1,j] ;

h [j]: =ms [1,j] ;

end;

FOR l: =1 to S do

begin

for j: =1 to s do

if m [j] =1 then

begin

k: =j;

for w: =1 to s do

begin

mh [w]: =mh [w] +MS [k,w] ;

if mh [w] >1 then mh [w]: =1;

end;

z: =0;

for j: =1 to s do

z: =z+mh [j] ;

if z=k1 then

begin

writeln (F1,'несвязна');

goto 1;

end;

k1: =z;

if z=s then

begin

writeln (F1,'связна');

Ny: =Ny+1;

goto 1;

end;

for j: =1 to s do

begin

m [j]: =mh [j] -h [j] ;

h [j]: =mh [j] ;

end;

writeln;

for i: =1 to s do

write (MS [n, i],' ');

writeln;

if z=s then writeln ('связна') else writeln ('несвязна');

writeln;

writeln ('Pн=',Ny/N: 1: 3);

writeln (F1,'Pн=',Ny/N: 1: 3);

close (F1);

readln;

end;

PROCEDURE MENU;

label ret;

var i,j,x: integer;

lin: integer;

s: array [1. .5] of string;

begin

key: =#0;

textbackground (7);

clrscr;

gotoxy (20,7);

textcolor (red);

write ('РАСЧЕТ СТРУКТУРНОЙ НАДЕЖНОСТИ СЕТИ РТС');

textcolor (white);

window (8,9,70,14);

textbackground (blue);

clrscr;

gotoxy (2,1); write ('+');

gotoxy (62,1); write ('+');

gotoxy (2,6); write ('+');

gotoxy (62,6); write ('+');

for j: =2 to 5 do

begin

gotoxy (2,j); write ('¦');

gotoxy (62,j); write ('¦');

end;

for i: =3 to 61 do

begin

gotoxy (i,1); write ('-');

gotoxy (i,6); write ('-');

end;

window (10,10,70,14);

textbackground (green);

textcolor (white);

s [1]: ='Количество узлов ';

s [2]: ='Количество испытаний ';

s [3]: ='Расчет ';

s [4]: ='Выход ';

writeln (s [1]);

textbackground (blue);

for x: =2 to 4 do

writeln (s [x]);

lin: =1;

repeat

repeat until keypressed;

if keypressed then

begin

key: =readkey;

if key=#0 then key: =readkey;

end;

if key=#80 then

begin

gotoxy (1,lin);

textbackground (blue);

write (s [lin]);

if lin<4 then lin: =lin+1 else lin: =1;

gotoxy (1,lin);

textbackground (green);

write (s [lin]);

end;

if key=#72 then

begin

gotoxy (1,lin);

textbackground (blue);

write (s [lin]);

if lin>1 then lin: =lin-1 else lin: =4;

gotoxy (1,lin);

textbackground (green);

write (s [lin]);

end;

if key=#13 then

begin

case lin of

1: kol_node;

2: kol_attemp;

3: number_attemp;

4: key: =#27;

end;

until (key=#27) or (key=#13);

window (1,1,80,25);

textbackground (black);

clrscr;

end;

BEGIN

repeat

MENU;

until key=#27;

end.

Приложение В

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ СТРУКТУРНОЙ НАДЕЖНОСТИ РАДИОТЕХНИЧЕСКИХ СИСТЕМ.

Проведем исследование трех типов структур систем связи: полносвязных, сотовых и иерархических. Полученные в результате исследования данные сведем в таблицу.

Таблица В. зависимость надежности РТС от надежности линии связи.

	Полносвязные	Сотовые	Иерархические
Р_Л.С.	Р_Н	Р_Н	Р_Н
0,1	0,286	0,123	0,028
0,3	0,507	0,292	0,131
0,5	0,654	0,443	0,248
0,7	0,761	0,619	0,407
0,9	0,907	0,863	0,772

Введение

Классификация структур радиотехнических систем

Одними из основных характеристик сетей связи, независимо от систем передачи информации, являются: структура, топология и структурная надежность.

Структура сети связи - взаимное расположение узлов коммуникаций и линий связи без учета их расположения на местности.

Топология сети связи - структура сети связи с учетом реального расположения узлов связи на местности.

Сеть считается связной, если все узлы коммуникаций можно соединить между собой цепью примыкающих друг к другу линий связи.

Структурная надежность сети связи - свойство сети обеспечивать связность сети в условиях выхода из строя ее элементов.

В качестве количественных оценок структуры сети связи, как правило, используются ‘S’ - количество узлов коммуникаций; ‘M’ - количество линий связи; ‘Kij’ - количество каналов в линии связи, соединяющей (‘i - й’ и ‘j - й’) узлы коммуникаций; ’Ri’ - степень узлов коммуникаций, которая показывает общее количество линий связи от данного узла к соседним (i,j=1…S, i≠j); U - сечение сети - минимальное число линий связи, одновременный отказ которых приводит к несвязной сети.

На сегодняшний день существует большое количество структур сетей, которые объединяют заданное множество узлов коммуникаций, однако среди них можно выделить три типа: сетеобразные, древовидные и кольцевые (таблица 1).

Кольцевые структуры имеют при ‘S’ узлов коммуникаций, ‘M’ линий связи и Ri=U. Капитальные затраты для создания сети связи кольцевой структуры относительно невелики. Однако, и структурная надежность такой сети также невысока. Так при выходе из строя всего двух не соседних узлов коммуникаций сеть остается не связной. Примером реализации кольцевой структуры являются локальная сеть ЭВМ БВК ЕС, созданная ВКЦП СО АН СССР.

К древовидным структурам сетей связи относятся все структуры имеющие M=S-1. Это звездообразные (U=1), линейные (U=1, Ri=2) и иерархические (U=1) структуры (таблица 1).

Отличительная особенность древовидных структур - минимальные капитальные затраты на их создания.

В линейных структурах все узлы коммуникаций, кроме оконечных, выполняют коммутационные функции. Примером построение таких сетей являются локальные сети ЭВМ: ИНФРА СО АН СССР и ETHERNET (США).

Звездообразная структура используется на уровне абонентских линий телефонных сетей связи, в терминальном комплексе NASDAQ (США) и в вычислительных сетях: ЭВС Латв. ССР и SNA (США).

Сетеобразные, в зависимости от их изображения на плоскости, различаются на плоские, которые не имеют пересекающихся линий связи; объемные, которые нельзя представить без пересечения линий связи.

Объемные, в зависимости от степени каждого узла коммутаций, могут быть полносвязными и неполносвязными.

В полносвязных структурах каждая пара узлов коммутаций соединена с линией связи, следовательно, Ri=U=S-1. Для ее построения необходимо иметь M=S (S-1) /2 линий связи. Структурная надежность таких сетей, по сравнению с другими (при равных S и вероятностях отказа каждого элемента сети), самая высокая. Однако, основным недостатком полносвязных сетей являются большие капитальные затраты. Примером построения таких сетей служит: международная сеть связи Почтового ведомства ФРГ или локальная сеть MERIT (США).

В неполносвязной структуре не каждая пара узлов коммуникаций соединена линией связи. Для построения при S узлов коммуникаций необходимо M=S*Rср. /2, где Rср. - средняя степень узлов коммуникаций сети. По количественным показателям (количество узлов коммутаций, линий связи, величина капитальных вложений на создания сети, структурная надежность, и U) неполносвязные и полносвязные структуры схожи. Примером применения неполносвязных структур являются сети ПДС.

Плоские сетеобразные структуры распадаются на ячеистые и радиально-кольцевые. Последние имеют высокую степень концентраций узлов коммуникаций в центре сети. При этом степень центрального узла коммутаций по отношению к остальным будет наивысшей.

Радиально-кольцевые структуры, как правило, применяются в сетях с явно выраженным характером тяготения удаленных узлов коммуникаций к центрую. Структурная надежность таких сетей, ввиду большого числа маршрутов между произвольной парой узлов коммуникаций, достаточно высокая. При этом капитальные затраты относительно небольшие.

Примером построения нерегулярных радиально-кольцевых структур (таблица 1) являются внутрисоюзные телефонные сети связи крупных городов.

Примеры реализации регулярных радиально-кольцевых структур неизвестны.

Ячеистые структуры (таблица 1) в отличии от радиально-кольцевых имеют относительно равномерное распределение узлов коммуникаций по всей площади сети связи. Каждый узел коммуникаций имеет сеть линий связи только с небольшим числом других узлов коммуникаций, как правило, ближних по расстоянию или имеющих большое тяготение. Из-за наличие большого числа маршрутов между произвольной парой узлов коммуникаций ячеистые структуры обладают достаточно высокой структурной надежностью при небольших капитальных затратах, по сравнению с объемными.

Ячеистые структуры различают регулярные и нерегулярные (таблица 1). К последним относятся структуры, в которых степень R i каждого узла коммуникаций различна. Для них количество линий связи M=S*Rср. /2. Примером таких сетей являются: локальная сеть ЭВМ СЕКОП АН СССР, вычислительные сети ARPA (США), CYCLADES (Франция), DATAPAC (Канада) и другие.

В ячеистых регулярных структурах каждый узел коммуникаций имеет степень: Ri = 3 (сотовая), Ri = 4 (квадратные) и Ri = 6 (треугольные). Для их создания необходимо M = Ri*S/2 линий связи.

Примером построения ячеистых регулярных квадратных структур является локальная сеть ЭВМ МИНИМАКС СО АН СССР.

Примеры реализации ячеистых регулярных сотовых и треугольных структур неизвестны.

Были рассмотрены основные структуры сетей связи, к которым можно свести произвольные путем выделения отдельных фрагментов, либо путем незначительных упрощений. Однако, реальные сети, как правило имеют смешанные структуры.

Таблица 1.

Типы структур сетей связи.

Сетеобразные.

Древовидные.

Плоские (планарные).

Объемные непланарные

Звездообразные.

Линейные.

Иерархические.

Кольцевые.

Ячеистые.

Радиально - кольцевые.

Полносвязные.

Неполносвязные.

Регулярные

Нерегулярные

Регулярные

Нерегулярные

Сотовые

Квадрат- ные

Треуголь-ные

Характеристики сети.

M=3S/2 Ri=4

M=2S Ri=4

M=3S Ri=6

M=SRср. /2

M=Sri/4 - 1

M=SRср. /2

M=S (S-1) /2 R=U=S - 1

M=Rср. S/2

M=S-1 U=1

M=S-1 U=1 Ri=2

M=S - 1 U=1

S=M U=Ri=2

Пример построения.

2. Методы исследования структурной надежности радиотехнических систем

Дата: 2019-07-30, просмотров: 207.

12 3 4 5 6 7 8 9 Следующая ⇒