Широко распространенным методом оценки надежности сложных технических систем является метод статистических испытаний. Однако для получения статистически достоверных результатов, особенно при высокой исходной надежности элементов системы и ее большой структурной избыточности, требуются значительные затраты машинного времени.

Опыт показывает, что основные затраты времени при статистических испытаниях сложной системы сопряжены с проверкой ее работоспособности в каждой реализации. При высокой исходной надежности p_i элементов или большой структурной, избыточности, характерной для разветвленных сетей коммутации, проверка на работоспособность подавляющего большинства реализации дает положительный результат, что обусловливает их малую информативность. Поэтому возникает естественное желание найти некоторое преобразование сети, позволяющее искусственно уменьшить исходную надежность ее элементов, чтобы быстрее набрать необходимую статистику отказов и получить обратное преобразование, позволяющее пересчитывать получаемые результаты на реальные показатели надежности элементов сети. Покажем, что такая возможность действительно существует.

Назовем разрезом подмножество элементов системы, удаление которых приводит к потере работоспособности. Рассмотрим некоторый разрез u, в который входит ровно z элементов. Частота выпадения такого разреза при статистических испытаниях стремится по ходу испытаний к ее вероятности:

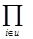P_u= p_i  (1-p_j).

Если обозначить через N общее число элементов сети, то вероятность Р_u можно записать в виде

P_u= ( 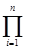p_i) 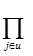 (1-p_j) / p_j.

Изменим исходные показатели надежности системы таким образом, чтобы каждый сомножитель (1-p_i) /p_j второго произведения увеличился в γ раз. Другими словами, вместо элемента с надежностью p_j введем элемент с надежностью p'_j такой, чтобы удовлетворялось условие

(1- p' _j) /p'_j=γ (1-p_j) /p_{j (}2.27)

При этом из (2.27) надежность нового элемента

p' _j= p_j [ p_j+ γ (1 - p_j)] ^-1 (2.28) '

Если произвести преобразование (2.27) для всех элементов сети, то вероятность выпадения разреза u в процессе испытаний изменится и составит

P_u= 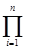p_j [ p_j+ γ (1 - p_j)] ^-1  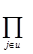γ (1-p_j) /p_j

Введем коэффициент δ увеличения частоты выпадания разреза

δ= P' _u/ P_u (2.29)

Подставляя в (2.29) старое и новое значения частоты выпадания разреза u, получаем

δ= 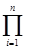p_j [ p_j+ γ (1 - p_j)] ^-1  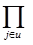γ.

Если в разрез u входит ровно z элементов, то

δ= γ^z 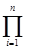p_j [ p_j+ γ (1 - p_j)] ^-1,

где второй сомножитель 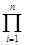p_j [p_j+ γ (1 - p_j)] ^-1=K константа для исходной системы. Коэффициент убыстрения можно представить в виде δ=γ^zK. Отсюда следует, что предлагаемое преобразование показателей надежности не приводит к нарушению относительной частоты появления разрезов фиксированного веса z, так как коэффициент убыстрения для всех этих разрезов одинаков. Однако относительная частота появления разрезов веса z+w по сравнению с разрезами веса z увеличивается в γ^w раз. Поэтому в ходе статистических испытаний преобразованной системы можно набрать достаточную статистику по разрезам большего веса, вероятность появления которых в исходной системе бывает обычно очень малой.

Пересчет вероятности появления разреза u из преобразованной системы в исходную производится в соответствии с (2.29):

P_u=P'_u/δ=P'_uγ^-zK^-1 (2.30)

Для выполнения обратного преобразования (2.30) кроме факта отказа системы необходимо фиксировать и вес z соответствующего разреза.

Из (6.30) следует, что каждый случай появления разреза u с весом z в преобразованной системе соответствует γ^-zK^-1 случаям появления такого же разреза в исходной системе. При этом если; д преобразованной системе за время испытаний произошло m отказов, то для исходной системы эквивалентное число отказов.

m_экв=K^-1 γ^-zi,

где z_i - число элементов, вышедших из строя при i-м отказе системы.

При возникновении очередного m-го отказа в преобразованной системе оценки надежности Р_m исходной системы уточняются в соответствии с выражением.

P_m=1-m_экв/M=1- (MK) - ¹ 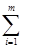γ^{- zi},

где М - общее число просмотренных реализации состояний преобразованной системы.

Возникает вопрос, каким следует выбирать параметр преобразования γ для максимального убыстрения. процесса статистических испытаний конкретной системы? Из (2.28) следует, что при γ=1 изменение исходной надежности не происходит и убыстрение отсутствует. Если выбрать γ слишком большим, то в преобразованной системе будут в основном возникать разрезы большого веса, не характерные для исходной системы, причем их вклад в результирующую надежность при больших z в соответствии с (2.30) будет невелик. Поэтому параметр γ следует выбирать таким образом, чтобы максимизировать вероятность возникновения наиболее "вероятных" разрезов.

Рассмотрим этот вопрос более подробно.

Для простоты положим, что показатели надежности всех элементов системы одинаковы и равны р. Обозначим через P (z) вероятность возникновения отказовых состояний веса z. Очевидно, что вероятность потери работоспособности системы

Q= 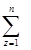P ( z). (2.31)

Обычно для реальных систем значение P (z) достаточно плавно меняется с увеличением веса разреза, поэтому в качестве наиболее вероятного разреза можно выбрать класс разрезов среднего веса.

Z_cp= [ 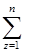zP ( z)] / 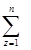P ( z).

Для надежных систем в выражении (2.31) можно пренебречь всеми членами, кроме первого ненулевого, соответствующего минимальному разрезу веса z₀, который и будет наиболее вероятным. Таким образом, задача состоит в том, чтобы максимизировать коэффициент убыстрения для наиболее вероятного разреза, т.е. найти максимум функции δ _(γ) при z=z_0, p_i=p, (i=1,2,…,N):

δ _{( γ)} = γ^z0 [ p+ γ (1- p)] ^{- N}. (2.32)

Из условия ∂δ _(γ) /∂γ=0 получаем оптимальное значение

γ₀= z₀ p [ ( N- z₀) / (1- p)] ^-1 (2.33)

Подставляя (2.33) в (2.28), нетрудно убедиться, что оптимальное значение γ₀ соответствует пересчитанному значению надежности элемента системы p'=1-z₀/N. Другими словами, для максимального убыстрения процедуры статистических испытаний необходимо таким образом пересчитать надежность элементов системы, чтобы средний вес отказов в преобразованной системе соответствовал весу наиболее вероятного разреза.

Убыстрение темпа набора статистики отказов в соответствии с (6.32) составит

δ_m={ z₀/ [ (1- p) N] } ^z0 [ ( N- z₀) / ( pN)] ^{N- z0}.

Так, для системы с параметрами p=0,99, N=20, z₀=3 время испытаний можно сократить приблизительно в 150 раз для достоверности получаемых результатов не хуже, чем в случае прямого набора статистики отказов системы.

Проведенные на ЭВМ сравнительные статистические испытания конкретных сетей по обычному и предлагаемому методам показали, что убыстрение сходимости результатов испытаний соответствует приведенным теоретическим оценкам.