Современные сети коммутации имеют весьма сложную структуру, которая в общем случае не сводится к последовательно-параллельным соединениям, поэтому для расчета надежности таких сетей нельзя применять методы, рассмотренные в §2.1 Прежде всего необходимо сформулировать критерий отказа сети. Через сеть обменивается информацией большое число пар абонентов, причем часто требуется, чтобы вероятность наличия связи между корреспондентами выделенной пары (r, l) была не менее заданной Р _rl. Под наличием связи понимается существование, по крайней мере, одного исправного пути между соответствующими узлами. Конечно, в сложной сети наличие исправного пути еще не гарантирует немедленного установления соединения, так как элементы этого пути могут быть заняты для обмена информацией других корреспондентов. Если, однако, предположить, что термин "наличие связи" относится только к информации высшей категории, доля которой в реальных сетях обычно весьма мала, и элементы любого исправного пути способны обеспечить обмен этой информацией в интересах всех корреспондентов, которые им могут воспользоваться, то возникает возможность рассматривать все пары корреспондентов независимо с точки зрения наличия связи между ними. В элементах сети, производительность которых недостаточна для обслуживания суммарной нагрузки высшей категории, можно предусмотреть согласно (2.7) или (2.8) большее число s рабочих компонентов.

Таким образом, сеть обладает заданной надежностью, если вероятность наличия связи или, как говорят, вероятность связности H_rl для каждой пары узлов не менее заданной Р _rl. В этих условиях расчет структурной надежности сети сводится к расчету вероятности связности между узлами. В дальнейшем рассмотрим и некоторые другие критерии надежности сети.

Итак, задана структура некоторой сети, состоящей из N элементов, причем надежность p_i каждого элемента известна (i= 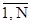). Необходимо определить вероятность связности относительно выделенной пары узлов r,l. Каждый элемент сети может находиться только в двух состояниях - исправен (И) или неисправен (H). При этом сеть может, очевидно, находиться в любом из S=2^N состояний. В некоторых из этих состояний сеть будет связна (С _rl) относительно рассматриваемых узлов. Если обозначить черезE_s вероятность того, что сеть находится в состоянии s, s=l, S, то искомая вероятность связности сети

H_rl= 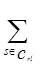E_s (2.9)

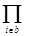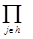где E_s= p_i  (1-p_i).

При этом по-прежнему предполагается, что отказы всех элементов сети - события независимые.

Рассмотренный метод расчета структурной надежности сети сопряжен с полным перебором ее состояний и при увеличении размеров сети быстро становится нереализуемым даже на современных быстродействующих ЭВМ.

Метод разложения

Несколько менее трудоемким является метод, основанный на разложении структуры сети относительно какого-нибудь ее элемента (метод разложения Шеннона-Мура). Идея этого метода заключается в том, чтобы свести анализируемую структуру к последовательно-параллельным соединениям и тем самым избежать полного перебора состояний. Для примера рассмотрим сеть простейшей структуры в виде мостика (рис.2.1).

Рисунок 2.1 Метод разложения

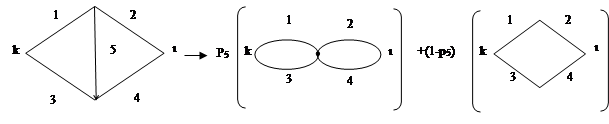Для простоты положим, что узлы этой сети идеально надежны, а ветви имеют конечную надежность р _i, i= 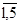. Нумерация ветвей приведена на рисунке. Проделаем с элементом под номером 5 ("перемычка" мостика) два опыта - "короткого замыкания", соответствующий исправному состоянию элемента, и "холостого хода", соответствующий его неисправному состоянию. Если перемычка находится в исправном состоянии, что случается с вероятностью p₅, то соединяемые ею узлы можно "стянуть" в смысле надежности (см. рис.2.1) и сеть будет иметь вид двух последовательно соединенных и параллельно включенных пар ветвей. Если перемычка находится в неработоспособном состоянии, что случается с вероятностью 1-p₅, то оставшаяся сеть будет иметь вид параллельного соединения цепочек.

Таким образом, мы "разложили" сеть относительно элемента 5, в результате чего получили две подсети с числом элементов на единицу меньше, чем в исходной сети. Поскольку обе подсети представляют собой последовательно-параллельные структуры, то, пользуясь формулами (2.3) и (2.4), можно сразу записать искомое выражение для вероятности связности сети относительно узлов r, l, используя для компактности обозначениеq_i=1-p_i.

H_rl=p₅ (1-q₁q₃) (1-q₂q₄) +q₅ [1- (1-q₁q₂) (1-q₃q₄)].

В более сложных структурах может потребоваться неоднократное применение теоремы разложения. Так, на рис.2.2 показано разложение относительно элемента 7 (верхняя строка), а затем по элементу 8 (нижняя строка). Получившиеся четыре подсети имеют последовательно-параллельные структуры и больше не требуют разложений. Легко видеть, что на каждом шаге число элементов в получающихся подсетях уменьшается на единицу а число подсетей, требующих дальнейшего рассмотрения удваивается. Поэтому описанный процесс в любом случае конечен, а число результирующих последовательно-параллельных структур составит 2^m, где т - число элементов, по которым пришлось провести разложение. Трудоемкость этого метода можно оценить величиной 2^m, что меньше трудоемкости полного перебора, но тем не менее все еще неприемлемо для расчета надежности реальных сетей коммутации.

Рисунок.2.2 Последовательное разложение сети