14. Задача синтеза для малых колебаний маятника. Здесь будет дано полное решение задачи синтеза оптимальных управлений для линейных объектов, описываемых уравнениями второго порядка. Фазовое пространство X в этом случае представляет собой плоскость.

Рассмотрим колебание плоского маятника. Как известно колебание маятника, подвешенного к точке опоры, описывается дифференциальным уравнением второго порядка:

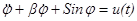(в нашем случае положим β=1)

при малых колебаниях маятника Sinφ≈φ тогда уравнение движения маятника запишется в виде:

                                                                             (3.1)

Управляющий параметр u (скалярный) будем предполагать изменяющимся в пределах -1£u£1.

Пусть 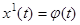— угол отклонения, а  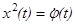— скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы:

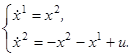                                                                         (3.2)

На плоскости x¹, x² «многогранник» U будет представляться отрезком [-1, 1], расположенным на оси x². Легко видеть, что ось x² не является собственным инвариантным подпространством матрицы A, которая для системы (3.2) имеет вид:

A= ,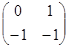

и потому условие общности положения всегда выполнено.

Найдём собственные значения матрицы A. Для этого составим характеристическое уравнение |λE─ A|=0, т. е. λ²+λ+1=0. Откуда находим, что собственные значения матрицы A такие:

т. е. собственные значения матрицы A комплексные. Введём обозначения 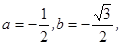 где b≠0.

Тогда матрица A преобразуется к виду:

= .

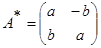Будем рассматривать систему, соответствующую матрице 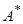, т. е. систему вида:

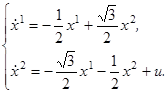                                                                (3.3)

Вначале рассмотрим соответствующую однородную систему:

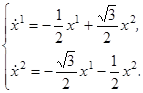                                                                      (3.4)

Общее решение этой системы имеет вид:

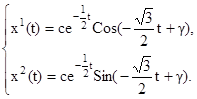
где c, γ – произвольные постоянные интегрирования.

Запишем функцию H и применим принцип максимума.

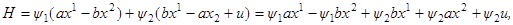
где ψ₁, ψ₂ определяются системой, сопряжённой к системе (3.3), т. е. системой вида:

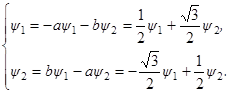                                                 (3.5)

Общее решение этой системы имеет вид:

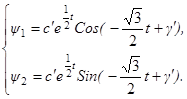
где c’, γ’ – произвольные постоянные интегрирования. Т. е. функция H имеет вид:

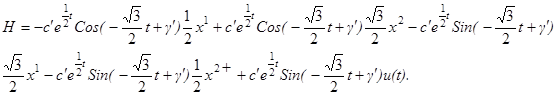
Подставим в функцию H представление решений x¹, x²:

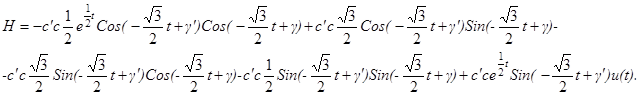
Т. к. собственный вектор матрицы A, соответствующий собственному значению l имеет вид q₁─iq₂, где q₁=(1;─1/2); q₂=(0;─ ).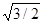

Пусть q₁ и q₂ – базисные векторы новой косоугольной системы координат y¹, y². Тогда переход от системы y¹, y² к системе x¹, x² выражается формулами:

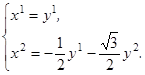
Тогда в новых координатах система уравнений (3.2) запишется в виде

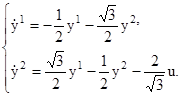
или, иначе, в виде

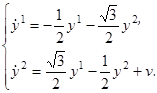
где v=(v¹, v²) ─ управляющая точка, которая может меняться в пределах многогранника V, представляющего собой отрезок [ 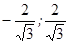] оси y².

Согласно теории вершинам e₁=(0, 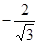), e₂=(0, 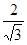) многогранника V соответствуют точки h₁=(1, - 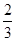), h₂=(-1, ) (координаты указаны в системе y¹, y²), а каждый из углов a₁, a₂, соответствующих этим вершинам, равен p.

Теперь уже нетрудно построить синтез оптимальных управлений в плоскости y¹, y². Кусками фазовых траекторий будут дуги логарифмических спиралей, т. к. у нас b=1, т. е. b>0 (рис. 18).

 При переходе от координат y¹, y² к координатам x¹, x² картина синтеза афинно искажается.

Список используемой литературы:

1. В.Г. Болтянский. «Математические методы оптимального управле­ния», М.: «Наука», 1968г.

2. Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. «Математическая теория оптимальных процессов», 4-е издательство. М.: «Наука», 1983г.

3. Р. Габасов, Ф.М. Кириллова. «Методы оптимизации», Минск, издательство БГУ, 1981г.