9. Формулировка задачи. Ниже будут подробно изучены управляемые объекты, движение которых описывается линейными дифференциальными уравнениями относительно величин x¹,…,xⁿ, u¹,…,u^r, т. е. уравнениями вида

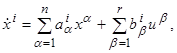 i=1,2,…,n,                                           (2.1)

где aⁱ_α и bⁱ_β ─ некоторые постоянные коэффициенты.

Одним из наиболее важных для приложений является случай, когда каждая из величин u¹, u²,…, u^r в уравнениях (2.1) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задаётся неравенствами

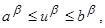 β=1,…,r.                                                                (2.2)

Как было указано выше (см. п. 4), эти неравенства определяют r-мерный параллелепипед.

В дальнейшем при рассмотрении объектов вида (2.1) будет предполагаться, что управляющий параметр u=(u¹, u²,…, u^r) может меняться в замкнутой области управления U, представляющей собой выпуклый многогранник (лежащий в пространстве переменных u¹, u²,…, u^r).

Для того чтобы записать уравнения (2.1) в векторной форме, мы введём в рассмотрение матрицы

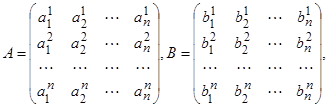                        (2.3)

элементами которых являются коэффициенты aⁱ_α, bⁱ_β, входящие в уравнения (2.1). Как обычно, результат применения матрицы A к вектору x=(x¹, x²,…, xⁿ) мы будем обозначать символом Ax, т. е. y=Ax есть n-мерный вектор, координаты которого определяются формулами

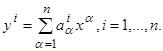                                                                 (2.4)

Аналогично для любого r-мерного вектора u=(u¹, u²,…, u^r) через Bu обозначается вектор, i-я координата которого равна 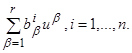 Таким образом, матрица A определяет линейное отображение координатного n-мерного пространства снова в n-мерное пространство, а матрица B определяет отображение r-мерного пространства в n-мерное.

Пользуясь матрицами A и B, мы можем теперь записать уравнения (2.1) в векторной форме:

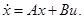                                                                                     (2.5)

Пусть u(t)=(u¹, u²,…, u^r) ─ произвольное допустимое (в смысле п. 4) управление, заданное на некотором отрезке t₀≤t≤t₁, и x₀=(x¹₀,…, xⁿ₀) ─ некоторая точка фазового пространства. Обозначим θ₁, θ₂,…, θ _k все точки, в которых хотя бы одна из функций u¹(t), u²(t),…, u^r(t) терпит разрыв, причём занумеруем эти точки таким образом, что t₀<θ₁<θ₂<…<θ _k<t₁. Подставив функции u¹(t), u²(t),…, u^r(t) в правые части системы (2.1),мы придём к системе уравнений

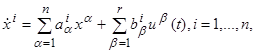                                          (2.6)

или в векторной форме,

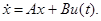                                                                                 (2.7)

Систему (2.7) мы рассмотрим сначала для значений t, удовлетворяющих неравенствам t₀≤t≤θ₁. На этом отрезке изменения аргумента существуют такие функции x¹(t),…, xⁿ(t), определённые и непрерывные на всём отрезке t₀≤t≤θ₁, которые, рассматриваемые на интервале t₀<t<θ₁, являются решениями системы (2.6) и, кроме того, удовлетворяют начальным условиям x¹(t₀)=x¹₀, x²(t₀)=x²₀,…, xⁿ(t₀)=xⁿ₀ (согласно сведениям из дифференциальных уравнений (см. книгу Л.С. Понтрягина «Обыкновенные дифференциальные уравнения», «Наука», М., 1965 (стр. 23, 24 и 168-172))).

Теперь мы можем рассмотреть систему (2.6) на отрезке θ₁≤t≤θ₂, воспользовавшись точкой γ₁=(x¹(θ₁),…, xⁿ(θ₁), θ₁) в качестве начального значения. На отрезке θ₁≤t≤θ₂ снова существует решение с начальным значением γ₁. Это решение мы снова обозначим через x(t)=(x¹(t),…, xⁿ(t)). Теперь функция x(t) построена на отрезке t₀≤t≤θ₂ и непрерывна на всём этом отрезке (и, в частности, в «точке сопряжения» θ₁;). Воспользовавшись, далее, новым начальным значением γ₂=(x¹(θ₂),…, xⁿ(θ₂), θ₂), мы продолжим эту функцию x(t) на отрезок θ₂≤t≤θ₃ и т. д. В конце концов мы определим x(t) на всём отрезке t₀≤t≤t₁.

Полученная функция x(t)=(x¹(t),…, xⁿ(t)) непрерывна на всём отрезке t₀≤t≤t₁ и является на нём кусочно-дифференцируемой; именно, во всех точках интервала t₀<t<t₁, кроме θ₁, θ₂,…, θ _k, функция x(t) непрерывно дифференцируема (и удовлетворяет системе (2.6)). Построенную функцию мы будем называть решением системы (2.6) (или уравнения (2.7)), соответствующим управлению u(t), при начальном условии x¹(t₀)=x¹₀, x²(t₀)=x²₀,…, xⁿ(t₀)=xⁿ₀. Наконец, мы будем говорить, что допустимое управление u(t), t₀≤t≤t₁, переводит фазовую точку из состояния x₀ в состояние x₁ (в силу закона движения (2.1) или (2.5)), если соответствующее ему решение x(t) системы (2.1), удовлетворяющее начальному условию x(t₀)=x₀, приходит в момент t₁ в точку x₁, т. е. удовлетворяет также «конечному» условию x(t₁)=x₁.

Теперь можно уточнить постановку задачи.

Линейной задачей оптимального управления мы будем называть задачу об отыскании оптимальных быстродействий в случае, когда выполнены следующие три условия:

1 ) уравнения движения объекта линейны (см. (2.1) или (2.5));

2 ) предписанное конечное состояние x₁ совпадает с началом координат (0, 0,…, 0) n-мерного фазового пространства переменных x¹, x²,…,xⁿ;

3 ) область управления U является r-мерным выпуклым многогранником в r-мерном пространстве (u¹, u²,…, u^r), причём начало координат этого пространства принадлежит многограннику U, но не является его вершиной.

Заметим, что начало координат xⁱ=0, i=1,…,n, является положением равновесия системы

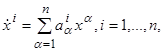                                                                 (2.8)

получающейся из системы (2.1) отбрасыванием управлений (т. е. получающейся из (2.1) при u¹= u²=…=u^r=0). Таким образом, условие 2) означает, что ищется управление, переводящее объект из заданного начального состояния x₀ в положение равновесия.

10. Принцип максимума. В пункте 6 мы сформулировали необходимое условие оптимальности, называемое принципом максимума. Данный пункт посвящён принципу максимума в случае линейной задачи оптимального управления. Вначале укажем те упрощения в формулировке принципа максимума, которые возникают в этом частном случае (т. е. в случае линейной задачи оптимального управления).

Заметим, прежде всего, что функция H (см. формулу (B) на стр. 10) принимает вид

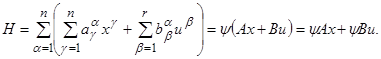           (2.9)

(Здесь в правой части записаны скалярные произведения; например, ψ Ax есть скалярное произведение векторов ψ и Ax.)

Далее, рассмотрим систему дифференциальных уравнений для вспомогательных переменных ψ₁, ψ₂,…, ψ _n (см. формулу (C) на стр. 10). Мы имеем

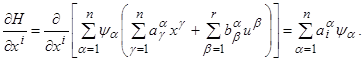
Следовательно, система уравнений для вспомогательных переменных принимает вид

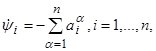                                                                 (2.10)

т. е. представляет собой так называемую сопряжённую систему (по отношению к линейной системе (2.8)). В векторной форме система (2.10) записывается в виде

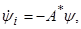                                                                                    (2.11)

где

─ матрица, получающаяся из матрицы A транспонированием (т. е. заменой строк столбцами).

Так как в правой части соотношения (2.9) первое слагаемое совсем не зависит от u, то при написании соотношения (D) (см. стр. 11) достаточно рассмотреть лишь второе слагаемое. Таким образом, соотношение (D) принимает в рассматриваемом случае вид

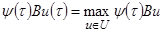                                                               (2.12)

для любого момента τ, t₀≤τ≤ t₁.

Наконец, соотношение (E) (стр. 11) становится просто ненужным, так как в рассматриваемом случае оно всегда выполняется. Действительно, так как x(t₁)=(0, 0,…, 0) (условие 2) на стр. 15), то в H(ψ(t₁), x(t₁), u(t₁)) первое слагаемое обращается в нуль (см. (2.9)). Второе же слагаемое, в силу (2.12), заведомо неотрицательно, ибо при u¹=…=u^r=0 (эта точка, в силу условия 3) на стр.15, принадлежит многограннику U) мы имеем ψ(τ)Bu=0, а потому максимальное значение выражения ψ(τ)Bu неотрицатнльно. Итак, соотношение H(ψ(t₁), x(t₁), u(t₁))³0 для линейной оптимальной задачи всегда выполнено.

Сказанное можно резюмировать следующим образом. Пусть u(t), t₀£t£t₁, - допустимое управление, переводящее объект (2.5) из заданного начального состояния x₀ в положение равновесия (0, 0,…, 0). Будем говорить, что управление u(t) удовлетворяет принципу максимума, если существует такое нетривиальное решение y(t) уравнения (2.11), для которого выполняется условие максимума (2.12) (в каждый момент времени t, t₀£t£t₁). Для оптимальности управления u(t) необходимо, чтобы оно удовлетворяло принципу максимума. Это и есть та упрощённая формулировка принципа максимума, к которой мы приходим в случае линейной задачи оптимального управления.

11. Принцип максимума — необходимое и достаточное условие оптимальности. Замечательным фактом является то, что в случае линейной задачи оптимального управления принцип максимума представляет собой не только необходимое, но и достаточное условие оптимальности. Однако факт этот имеет место не для произвольной линейной задачи — имеются малосущественные исключения. Поэтому мы наложим на линейную задачу некоторое ограничение, называемое условием общности положения. Сформулируем это условие:

Условие общности положения: если w — вектор, параллельный произвольному ребру многогранника U, то вектор B w не принадлежит никакому собственному инвариантному подпространству относительно преобразования A. Невыполнение условия общности положения означает, что хотя бы для одного ребра многогранника U векторы B w, AB w, A²B w,…, A^n-1B w линейно зависимы, т. е. определитель n-го порядка, составленный из координат этих векторов, обращается в нуль. Однако всюду в дальнейшем условие общности положения предполагается (если не оговорено противное) выполненным.

Теперь перейдём к теореме, упоминавшейся в начале этого пункта.

Т е о р е м а 2.1. Пусть u(t), t₀£t£t₁, — допустимое управление, переводящее объект из заданного начального состояния x₀ в положение равновесия (0, 0,…, 0). Для оптимальности управления u(t) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума.