Тема: Синтез оптимальных уравнений

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Механико-математический факультет

Кафедра теоретической механики и робототехники

Курсовая работа

Тема: Синтез оптимальных уравнений

Студента 3-го курса 13 группы

Павловского Сергея Александровича

Научный руководитель

Лютов Алексей Иванович

Минск 2001г.

ОГЛАВЛЕНИЕ

Г л а в а I. Введение................................................................................................ 2

§ 1. Задача об оптимальном быстродействии.................................................... 2

1.Понятие об оптимальном быстродействии.................................................. 2

2.Задача управления........................................................................................ 3

3.Уравнения движения объекта....................................................................... 5

4.Допустимые управления............................................................................... 6

§ 2. Об основных направлениях в теории оптимальных процессов.................. 7

5.Метод динамического программирования.................................................. 7

6.Принцип максимума..................................................................................... 9

§ 3. Пример. Задача синтеза............................................................................... 12

7.Пример применения принципа максимума............................................... 12

8.Проблема синтеза оптимальных управлений............................................ 14

Г л а в а II. Линейные оптимальные быстродействия..................................... 15

§ 4 Линейная задача оптимального управления............................................... 15

9.Формулировка задачи................................................................................ 15

10.Принцип максимума................................................................................. 16

11.Принцип максимума — необходимое и достаточное условие

оптимальности............................................................................................... 17

12.Основные теоремы о линейных оптимальных быстродействиях........... 18

§ 5. Решение задачи синтеза для линейных задач второго порядка................ 18

13.Упрощение уравнений линейного управляемого объекта...................... 18

Г л а в а III. Синтез оптимальных управлений для уравнения второго

порядка.......................................................................................................... 20

§ 6. Решение задачи синтеза в случае комплексных собственных значений...... 20

14.Задача синтеза для малых колебаний маятника...................................... 20

Список используемой литературы....................................................................... 23

Г л а в а I

ВВЕДЕНИЕ

Управляемые объекты прочно вошли в нашу повседневную жизнь и стали обиходными, обыденными явлениями. Мы видим их буквально на каждом шагу: автомобиль, самолёт, всевозможные электроприборы, снабжённые регуляторами (например, электрохолодильник), и т. п. Общим во всех этих случаях является то, что мы можем «управлять» объектом, можем в той или иной степени влиять на его поведение.

Обычно переход управляемого объекта из одного состояния в другое может быть осуществлён многими различными способами. Поэтому возникает вопрос о выборе такого пути, который с некоторой (но вполне определённой) точки зрения окажется наиболее выгодным. Это и есть (несколько расплывчато сформулированная) задача об оптимальном управлении.

Пример. Задача синтеза

7. Пример применения принципа максимума. В этом пункте мы разберём один пример вычисления оптимальных процессов. Именно, рассмотрим управляемый объект, упомянутый в п. 3 (см. уравнения (1.1)), при условии, что сила трения и упругая сила отсутствуют (т. е. b=0, k=0), масса m равна единице (m=1), а управляющий параметр подчинён ограничениям |u|≤1. Иначе говоря, мы рассматриваем материальную точку G массы m=1 (см. рис. 10), свободно и без трения движущуюся по горизонтальной прямой и снабжённую двигателем, развивающим силу u, где |u|≤1. Согласно (1.1) уравнения движения этого объекта имеют вид:

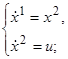(1.29)

─1≤u≤1. (1.30)

Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из заданного начального состояния x₀=(x₀¹, x₀²). Иначе говоря, будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит точка x₁=(0, 0). Механически это означает, что материальную точку, имеющую заданное положение x₀¹ и заданную начальную скорость x₀², мы хотим за кратчайшее время привести в начало отсчёта с нулевой скоростью (т. е. добиться того, чтобы точка пришла в начало отсчёта и остановилась там).

Функция H в рассматриваемом случае имеет вид

H=ψ₁x²+ψ₂u (1.31)

(см. (1.29) и (B)). Далее, для вспомогательных переменных ψ₁, ψ₂ мы получаем систему уравнений 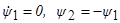. Из этой системы уравнений находим: ψ₁=d₁; ψ₂= ─d₁t+ d₂, где d1, d₂ ─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30):

u(t)= +1, если ψ₂(t)>0; u(t)= ─1, если ψ₂(t)<0.

Иначе говоря, u(t)=sign ψ₂(t)=sign (─ d₁t + d₂). Отсюда следует, что каждое оптимальное управление u(t), t₀≤t≤t₁, является кусочно-постоянной функцией, принимающей значения 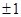и имеющей не более двух интервалов постоянства (ибо линейная функция ─d₁t + d₂ не более одного раза меняет знак на отрезке t₀≤t≤t₁).

Для отрезка времени, на котором u 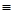1, мы имеем (в силу системы (1.29)) 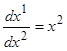, откуда находим

x¹=1/2(x²)²+c. (1.32)

Таким образом, кусок фазовой траектории, для которого u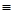

1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении оси x¹). По этим параболам фазовые точки движутся снизу вверх (ибо

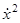= u 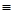1, т. е.

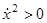Аналогично для отрезка времени, на котором u 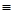─1, мы имеем, откуда находим

x¹= ─1/2(x²)²+ c’. (1.33)

Семейство парабол (1.33) (также получающихся друг из друга сдвигом в направлении оси x¹) показано на рис. 14. По параболам (1.33) фазовые точки движутся сверху вниз (ибо )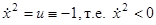

Как было указано выше, каждое оптимальное управление u(t) является кусочно-постоянной функцией, принимающей значения

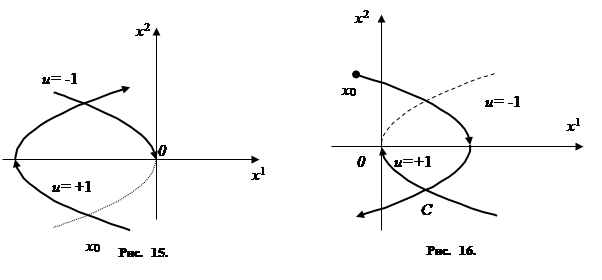
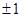и имеющей не более двух интервалов постоянства. Если управление u(t) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u= ─1, а затем u= +1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u.

На рис. 17 изображено всё семейство полученных таким образом фазовых траекторий (здесь AO ─ дуга параболы x¹=1/2(x²)², расположенная в нижней полуплоскости; BO ─ дуга параболы x¹= ─1/2(x²)², расположенная в верхней полуплоскости).

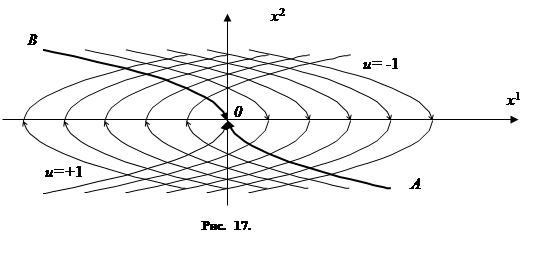Итак, согласно принципу максимума только изображённые на рис. 17 траектории могут быть оптимальными, причём видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (т. е. задание начальной точки x₀ однозначно определяет соответствующую траекторию).

8. Проблема синтеза оптимальных управлений. Посмотрим на разобранный в предыдущих пунктах пример с несколько иной точки зрения. Найденное выше решение оптимальной задачи можно истолковать следующим образом. Обозначим через v(x)= +1 ниже линии AOB и на дуге AO, v(x)= ─1 выше линии AOB и на дуге BO. Тогда (см. 17) на каждой оптимальной траектории значение u(t) управляющего параметра (в произвольный момент времени t) равно v(x(t)), т. е. равно значению функции v в той точке, в которой в момент t находится движущаяся фазовая точка, пробегающая оптимальную траекторию u(t)=v(x(t)). Это означает, что, заменив в системе (1.29) величину u функцией v(x), мы получим систему

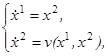(1.34)

решение которой (при произвольном начальном состоянии x₀) даёт оптимальную фазовую траекторию, ведущую в начало координат. Иначе говоря, система (1.34) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.

Рассмотренный пример показывает, что решение задачи об оптимальных управлениях естественно ожидать в следующей форме. Будем решать оптимальную задачу в общей постановке:

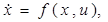
(см. п. 3), рассматривая всевозможные начальные состояния и каждый раз предписывая в качестве конечного состояния начало координат O фазового пространства. Тогда (насколько можно судить по разобранному выше примеру) существует такая функция v(x), заданная в фазовом пространстве V принимающая значения в области управления U, что уравнение

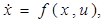(1.35)

определяет все оптимальные траектории, ведущие в начало координат. Иначе говоря, оптимальное управление оказывается естественным искать не в форме u= u(t), а в форме u= v(x), т. е. искомое оптимальное управление в каждый момент зависит лишь от того, в какой точке пространства находится в данный момент фазовая точка.

Функцию v(x), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией, а задачу нахождения синтезирующей функции ─ задачей синтеза оптимальных управлений. В разобранном примере синтезирующая функция была кусочно-непрерывной (даже кусочно-постоянной).

Г л а в а II

Г л а в а III