Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

5. Метод динамического программирования. Для управляемого объекта, описанного в предыдущем параграфе, мы рассмотрим задачу об оптимальном переходе ─ в смысле быстродействия ─ из фазового состояния x в фазовое состояние x₁. При этом конечную фазовую точку x₁ будем считать фиксированной, а в качестве начальной точки x будем рассматривать различные точки фазового пространства. Мы будем предполагать в этом пункте, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:

Г и п о т е з а 1. Какова бы ни была отличная от x₁ точка x фазового пространства, существует оптимальный (в смысле быстродействия) процесс перехода из точки x₀ в точку x₁ (рис. 6).

Время, в течение которого осуществляется оптимальный переход из точки x₀ в точку x₁, обозначим через T( x). В дальнейших рассуждениях будет удобно вместо T( x) ввести функцию ω(x), отличающуюся от неё знаком

ω(x)= ─T(x).                                                                                     (1.8)

Так как каждая точка x фазового пространства имеет координаты x¹,…, xⁿ, то ω(x)= ─T( x) является функцией от n переменных, т. е. ω(x)= ω(x¹,…, xⁿ). Поэтому имеет смысл говорить о непрерывности этой функции (по совокупности переменных x¹,…, xⁿ) и о дифференцируемости этой функции по каждой из переменных x¹,…, xⁿ.

А также будем предполагать, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:

Г и п о т е з а 2. Функция ω(x) непрерывна и всюду, кроме точки x₁, имеет непрерывные частные производные

Пусть теперь x₀ ─ произвольная отличная от x₁ точка фазового пространства, а u₀ ─ произвольная точка области U. Предположим, что объект находится в момент t₀ в фазовом состоянии x₀ и движется в течение некоторого времени под воздействием постоянного управления u= u₀. Фазовую траекторию объекта при этом движении обозначим через y(t)=(y¹( t),…, yⁿ( t)). Таким образом, фазовая траектория y( t) при t> t₀ удовлетворяет уравнениям

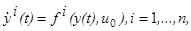                                                          (1.9)

(см. (1.2), (1.3)) и начальному условию

y(t₀)=x₀.                                                                                           (1.10)

Если мы будем двигаться из точки x₀ до точки y( t) (по рассматриваемой фазовой траектории), то затратим на это движение время t ─ t₀. Двигаясь затем из точки y( t) оптимально, мы затратим на движение от точки y(t) до точки x₁ время T( y( t)). В результате мы совершим переход из точки x₀ в точку x₁, затратив на этот переход время (t ─ t₀)+T(y(t)). Но так как оптимальное время движения от точки x₀ до точки x₁ равно T(x₀), т. е. равно T(y(t₀)), то T(y(t₀))≤(t ─ t₀)+T(y(t)). Заменяя функцию T через ω (см. (1.8)) и разделив обе части неравенства на положительную величину t ─ t₀, получаем отсюда 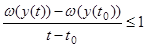и поэтому, переходя к пределу при t→ t₀, находим

│_при 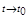≤1.                                                                  (1.11)

Но производная, указанная в левой части этого неравенства, вычисляется по формуле полной производной 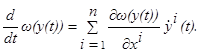 Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид  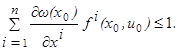Точки x₀, u₀ здесь были произвольными. Таким образом, для любой (отличной от x₁) точки x фазового пространства и любой точки u области управления U выполнено соотношение

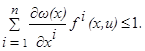                                                                    (1.12)

Пусть теперь (u(t), x(t)) ─ оптимальный процесс, переводящий объект из фазового состояния x₀ в состояние x₁, и t₀≤t≤t₁ ─ отрезок времени, в течение которого это оптимальное движение происходит, так что x(t₀)= x₀, x(t₁)=x₁ и t₁=t₀ + T(x₀). Движение по рассматриваемой оптимальной траектории от точки x₀ до точки x(t) осуществляется в течение времени t ─ t₀, а движение от точки x(t) до точки x₁ ─ в течение времени T(x₀) ─ (t ─ t₀). Быстрее, чем за время T(x₀) ─ (t ─ t₀), из точки x(t) попасть в точку x₁ невозможно. Итак, T(x₀) ─ (t ─ t₀) есть время оптимального движения из точки x(t) в точку x₁, т. е. T(x(t))= T(x₀) ─ (t ─ t₀). Заменив здесь T через ω, т. е. ω(x(t))= ω(x₀) + t ─ t₀) и взяв производную по t, получаем

 t₀≤t≤t₁.            (1.13)

Таким образом, для каждого оптимального процесса в течение всего движения выполняется равенство (1.13).

Если мы теперь введём в рассмотрение функцию

B(x, u(t))= 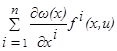,                                                         (1.14)

То соотношения (1.12) и (1.13) могут быть записаны следующим образом:

B(x, u)≤1 для всех точек x≠x₁ и u;                                                (1.15)

B(x, u)≡1 для любого оптимального процесса (u(t), x(t)).         (1.16)

Итак, справедлива следующая

Т е о р е м а 1.1. Если для управляемого объекта, описываемого уравнением (1.5) и предписанного конечного состояния x₁ выполнены гипотезы 1 и 2, то имеют место соотношения (1.15) и (1.16) (оптимальность понимается в смысле быстродействия).

Эта теорема и составляет сущность метода динамического программирования для рассматриваемой задачи. Эту теорему можно сформулировать и несколько иначе. Написав соотношение (1.16)

Для t=t₀, получим B(x₀, u(t₀))=1, т. е. для любой точки x₀ (отличной от x₁) найдётся в U такая точка u (а именно u= u(t₀)), что B(x₀, u)=1. В сопоставлении с неравенством (1.15) получаем соотношение

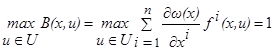 для любой точки x≠x₁.    (1.16^*)

Метод динамического программирования (1.15), (1.16) (или, что то же самое, (1.16^*), (1.16)) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции ω(x), так как эта функция входит в соотношения (1.15) ─ (1.16^*). Во-вторых, уравнение Беллмана (1.16^*) (или соотношения (1.15), (1.16)) представляет собой уравнение в частных производных относительно функции ω, осложнённое к тому же знаком максимума. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1 и 2. Ведь оптимальные управления и функция ω нам заранее не известны, так что гипотезы 1 и 2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно. Этот недостаток можно было бы считать не особенно существенным, если бы после решения оптимальной задачи этим методом оказалось, что функция ω(x) действительно является непрерывно дифференцируемой. Но дело заключается в том, что даже в простейших, линейных задачах оптимального управления функция ω(x) не является, как правило, всюду дифференцируемой. Тем не менее, методом динамического программирования можно нередко пользоваться как ценным эвристическим средством.

6. Принцип максимума. Продолжим теперь рассуждения предыдущего пункта, предположив функцию ω(x) уже дважды непрерывно дифференцируемой (всюду, кроме точки x₁). Итак, будем предполагать, что выполнена следующая

Г и п о т е з а 3. функция ω(x) имеет при x≠ x₁ вторые непрерывные производные 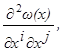i, j=1,2,…,n, а функции fⁱ(x, u) ─ первые непрерывные производные  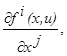где i, j=1,2,…,n.

Пусть (u( t), x( t)), t₀≤t≤t₁, ─ оптимальный процесс, переводящий объект (1.2) (или (1.3)) из фазового состояния x₀ в состояние x₁. Фиксируем некоторый момент времени t, t₀≤t≤t₁, и рассмотрим функцию B(x, u(t))= 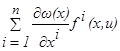 переменного x. В силу гипотезы 3 вытекает, что функция B(x, u(t)) всюду, кроме точки x₁, имеет непрерывные производные по переменным x¹,x²,…,xⁿ:

  (1.17)

В частности, так как x(t)≠x₁ (поскольку t<t₁), то функция B(x, u(t)) имеет вблизи точки x=x(t) непрерывные производные по переменным x¹,x²,…,xⁿ. Далее, мы имеем в силу (1.15), (1.16) B(x, u(t))≤1 для любого x≠ x₁; B(x, u(t))=1 при x= x(t).

Эти два соотношения означают, что функция B(x, u(t)) достигает в точке x=x(t) максимума, и потому её частные производные по x¹,…, xⁿ обращаются в нуль в этой точке:

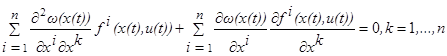(1.18)

Кроме того, дифференцируя функцию 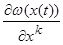 по t, находим

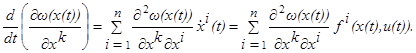
Поэтому соотношение (1.18) может быть переписано в следующем виде:

             (1.19)

Заметим теперь, что в формулы (1.15), (1.16), (1.17) и (1.19) сама функция ω не входит, а входят только её частные производные 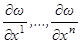. Поэтому мы введём для удобства следующие обозначения:

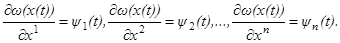                   (1.20)

Тогда функция B (см. (1.14)) записывается таким образом:

B(x(t), u(t))=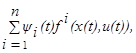

и соотношение (1.16) принимает вид

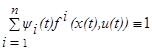, для оптимального процесса (x(t), u(t)), t₀≤t<t₁.     (1.21)

Кроме того, согласно (1.15)

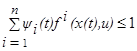 для любой точки u 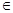U и всех t₀≤t<t₁.       (1.22)

 

 

Наконец, соотношения (1.19) записываются следующим образом:

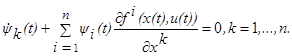                               (1.23)

Итак, если (u(t), x(t)), t₀≤t<t₁, ─ оптимальный процесс, то существуют такие функции ψ₁(t), ψ₂(t),…, ψ _n(t) (они определяются равенствами (1.20)), что имеют место соотношения (1.21), (1.22), (1.23).

Рассмотрение левых частей соотношений (1.21), (1.22) подсказывает нам, что целесообразно ввести в рассмотрение следующую функцию:

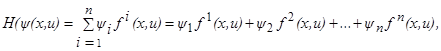            (1.24)

зависящую от 2n+ r аргументов ψ₁, ψ₂,…, ψ _n, x¹,…, xⁿ, u¹,…, u^r. С помощью этой функции соотношения (1.21), (1.22) записываются в следующем виде:

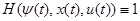для оптимального процесса (u(t), x(t)), t₀≤t<t₁,       (1.25)

где ψ(t)=(ψ₁(t),…,ψ _n(t)) определяются равенствами (1.20);

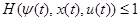для любой точки u 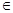U и всех t₀≤t<t₁.                         (1.26)

Вместо неравенства (1.26) мы можем в силу (1.25) написать следующее соотношение:

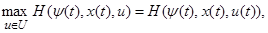 t₀≤t<t₁.                         (1.27)

Наконец, соотношения (1.23) можно, очевидно, переписать так:

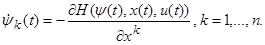                                      (1.28)

Итак, если (u(t), x(t)), t₀≤t<t₁, ─ оптимальный процесс, то существует такая функция ψ(t)=(ψ₁(t),…, ψ _n(t)), что выполняются соотношения (1.25), (1.27), (1.28), где функция H определяется соотношением (1.24).

Так как в соотношениях (1.24), (1.25), (1.27), (1.28) нигде не участвует явно функция ω(x), то равенства (1.20), выражающие функции ψ₁(t),…, ψ _n(t) через ω, никаких добавочных сведений не дают, и о них можно забыть, ограничившись утверждением, что какие-то функции ψ₁(t),…, ψ _n(t), удовлетворяющие перечисленным соотношениям (1.25), (1.27), (1.28), существуют. Соотношения (1.28) представляют собой систему уравнений, которым эти функции удовлетворяют. Заметим, что функции ψ₁(t),…, ψ _n(t) составляют нетривиальное решение этой системы (т. е. ни в какой момент времени t все эти функции одновременно в нуль не обращаются); действительно, если бы при некотором t было ψ₁(t)= ψ₂(t)=…=ψ _n(t)=0, то в силу (1.24) мы получили бы H(ψ(t), x(t), u(t))=0, что противоречит равенству (1.25). Таким образом, мы получаем следующую теорему, которая носит название принципа максимума.

Т е о р е м а 1.2. Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением (в векторной форме)

                                                                              (A)

и предписанного конечного состояния x₁ выполнены гипотезы 1, 2 и 3. Пусть (u(t), x(t)), t₀≤t≤t₁, ─ некоторый процесс, переводящий объект из начального состояния x₀ в состояние x₁. Введём в рассмотрение функцию H, зависящую от переменных x¹(t),…, xⁿ(t), u¹,…, u^r и некоторых вспомогательных переменных ψ₁(t),…, ψ _n(t) (см. (1.24)):

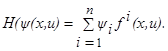                                                                  (B)

С помощью этой функции H запишем следующую систему дифференциальных уравнений для вспомогательных переменных:

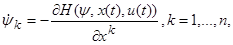                                                  (C)

где (u(t), x(t)) ─ рассматриваемый процесс (см. (1.28)). Тогда, если процесс (u(t), x(t)), t₀≤t<t₁, является оптимальным, то существует такое нетривиальное решение ψ(t)=(ψ₁(t),…, ψ _n(t)), t₀≤t<t₁, системы (C), что для любого момента t, t₀≤t<t₁, выполнено условие максимума

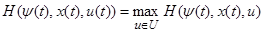                                          (D)

(см. (1.27)) и условие (1.25) H(ψ(t),x(t),u(t))=1.

Однако в приведённой здесь форме принцип максимума страдает одним недостатком: он выведен в предположение дифференцируемости (и даже двукратной) функции ω(x), а эта функция в действительности не является (в обычно встречающихся случаях) всюду дифференцируемой.

Из-за предположения о выполнении сформулированных гипотез (о функции ω(x)) принцип максимума в том виде, в каком он сформулирован выше, не является удобным условием оптимальности. По форме он выведен как необходимое условие оптимальности: если процесс оптимален, то выполнено соотношение (1.16^*) и соответственно (D), т. е. выполнение этого условия необходимо для оптимальности. Однако это условие выведено лишь в предположении выполнения гипотез 1, 2, 3, а их выполнение отнюдь не необходимо для оптимальности. Вот почему сформулированные выше теоремы не могут считаться необходимыми условиями оптимальности.

Замечательным, однако, является тот факт, что если в теореме 1.2 решение ψ(t) и условие максимума (D) рассматривать на всём отрезке t₀≤t≤t₁ (а не только при t₀≤t<t₁), а заключительное условие

H(ψ(t₁), x(t₁), u(t₁))≥0,                                                                        (E)

то в этой форме принцип максимума будет справедлив без каких бы то ни было предположений о функции ω, т. е. принцип максимума станет весьма удобным и широко применимым необходимым условием оптимальности.

Пример. Задача синтеза

7. Пример применения принципа максимума. В этом пункте мы разберём один пример вычисления оптимальных процессов. Именно, рассмотрим управляемый объект, упомянутый в п. 3 (см. уравнения (1.1)), при условии, что сила трения и упругая сила отсутствуют (т. е. b=0, k=0), масса m равна единице (m=1), а управляющий параметр подчинён ограничениям |u|≤1. Иначе говоря, мы рассматриваем материальную точку G массы m=1 (см. рис. 10), свободно и без трения движущуюся по горизонтальной прямой и снабжённую двигателем, развивающим силу u, где |u|≤1. Согласно (1.1) уравнения движения этого объекта имеют вид:

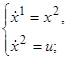                                                                                       (1.29)

─1≤u≤1.                                                                                          (1.30)

Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из заданного начального состояния x₀=(x₀¹, x₀²). Иначе говоря, будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит точка x₁=(0, 0). Механически это означает, что материальную точку, имеющую заданное положение x₀¹ и заданную начальную скорость x₀², мы хотим за кратчайшее время привести в начало отсчёта с нулевой скоростью (т. е. добиться того, чтобы точка пришла в начало отсчёта и остановилась там).

Функция H в рассматриваемом случае имеет вид

H=ψ₁x²+ψ₂u                                                                                    (1.31)

(см. (1.29) и (B)). Далее, для вспомогательных переменных ψ₁, ψ₂ мы получаем систему уравнений 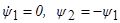. Из этой системы уравнений находим:  ψ₁=d₁; ψ₂= ─d₁t+ d₂, где d1, d₂ ─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30):

u(t)= +1, если ψ₂(t)>0; u(t)= ─1, если ψ₂(t)<0.

Иначе говоря, u(t)=sign ψ₂(t)=sign (─ d₁t + d₂). Отсюда следует, что каждое оптимальное управление u(t), t₀≤t≤t₁, является кусочно-постоянной функцией, принимающей значения 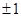 и имеющей не более двух интервалов постоянства (ибо линейная функция ─d₁t + d₂ не более одного раза меняет знак на отрезке t₀≤t≤t₁).

Для отрезка времени, на котором u 1, мы имеем (в силу системы (1.29)) 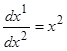, откуда находим

x¹=1/2(x²)²+c.                                                                                  (1.32)

Таким образом, кусок фазовой траектории, для которого u 1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении оси x¹). По этим параболам фазовые точки движутся снизу вверх (ибо 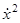= u 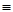1, т. е. ).

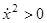Аналогично для отрезка времени, на котором u 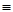 ─1, мы имеем, откуда находим

x¹= ─1/2(x²)² + c’.                                                                           (1.33)

Семейство парабол (1.33) (также получающихся друг из друга сдвигом в направлении оси x¹) показано на рис. 14. По параболам (1.33) фазовые точки движутся сверху вниз (ибо )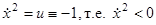

Как было указано выше, каждое оптимальное управление u(t) является кусочно-постоянной функцией, принимающей значения 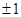 и имеющей не более двух интервалов постоянства. Если управление u(t) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u= ─1, а затем u= +1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u.

На рис. 17 изображено всё семейство полученных таким образом фазовых траекторий (здесь AO ─ дуга параболы x¹=1/2(x²)², расположенная в нижней полуплоскости; BO ─ дуга параболы x¹= ─1/2(x²)², расположенная в верхней полуплоскости).

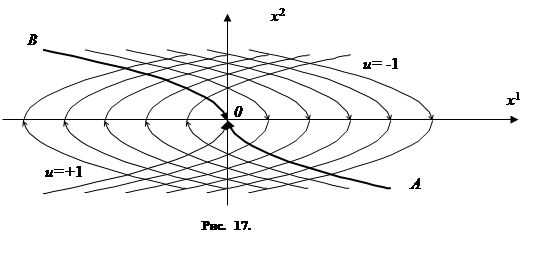Итак, согласно принципу максимума только изображённые на рис. 17 траектории могут быть оптимальными, причём видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (т. е. задание начальной точки x₀ однозначно определяет соответствующую траекторию).

8. Проблема синтеза оптимальных управлений. Посмотрим на разобранный в предыдущих пунктах пример с несколько иной точки зрения. Найденное выше решение оптимальной задачи можно истолковать следующим образом. Обозначим через v(x)= +1 ниже линии AOB и на дуге AO, v(x)= ─1 выше линии AOB и на дуге BO. Тогда (см. 17) на каждой оптимальной траектории значение u(t) управляющего параметра (в произвольный момент времени t) равно v(x(t)), т. е. равно значению функции v в той точке, в которой в момент t находится движущаяся фазовая точка, пробегающая оптимальную траекторию u(t)=v(x(t)). Это означает, что, заменив в системе (1.29) величину u функцией v(x), мы получим систему

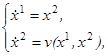                                                                             (1.34)

решение которой (при произвольном начальном состоянии x₀) даёт оптимальную фазовую траекторию, ведущую в начало координат. Иначе говоря, система (1.34) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.

Рассмотренный пример показывает, что решение задачи об оптимальных управлениях естественно ожидать в следующей форме. Будем решать оптимальную задачу в общей постановке:

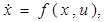
(см. п. 3), рассматривая всевозможные начальные состояния и каждый раз предписывая в качестве конечного состояния начало координат O фазового пространства. Тогда (насколько можно судить по разобранному выше примеру) существует такая функция v(x), заданная в фазовом пространстве V принимающая значения в области управления U, что уравнение

                                                                             (1.35)

определяет все оптимальные траектории, ведущие в начало координат. Иначе говоря, оптимальное управление оказывается естественным искать не в форме u= u(t), а в форме u= v(x), т. е. искомое оптимальное управление в каждый момент зависит лишь от того, в какой точке пространства находится в данный момент фазовая точка.

Функцию v(x), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией, а задачу нахождения синтезирующей функции ─ задачей синтеза оптимальных управлений. В разобранном примере синтезирующая функция была кусочно-непрерывной (даже кусочно-постоянной).

Г л а в а II