13. Упрощение уравнений линейного управляемого объекта. Нередко бывает, что в линейной задаче общая запись уравнений движения объекта в виде (2.1) неудобна и целесообразно воспользоваться некоторыми упрощениями. Мы здесь отметим стандартные упрощения, которые можно осуществить с помощью замены координат.

q Прежде всего, рассмотрим вопрос о замене координат в фазовом пространстве X рассматриваемого управляемого объекта. Предположим, что в пространстве X вместо координат x¹,…, xⁿ введены новые координаты y¹,…, yⁿ, связанные с прежними координатами соотношениями

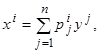
                                                   (2.13)

(где матрицы P=(pⁱ_j) и Q=(qⁱ_j) взаимно обратны). Ясно, что при такой замене линейная система (2.1) превращается в новую линейную систему

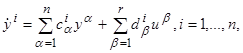
коэффициенты которой легко вычисляются:

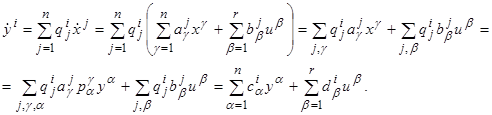
Таким образом, ,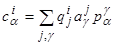      

Переходя к векторным обозначениям, можно сказать, что указанная замена координат переводит уравнение (2.5) в уравнение 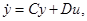 где матрицы C и D выражаются через матрицы A, B, P, Q по формулам C=QAP, D=QB.

Очевидно, при такой замене условия 1), 2), указанные на стр. 15, сохраняются и для уравнения 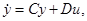 получаемого после замены. Далее, каждый процесс (u(t), x(t)), удовлетворяющий уравнению  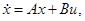переходит в процесс (u(t), y(t)), удовлетворяющий уравнению  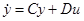(и обратно). Так как при этом время t не меняется, то указанная замена переводит оптимальные процессы для уравнения 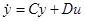(и наоборот). В частности, синтез оптимальных управлений для уравнения  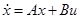переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения .

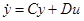Таким образом, если уравнение окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения . В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A трансформированной матрицей C=QAP, в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A, составленной из коэффициентов при фазовых координатах.

q Предположим, что в уравнении 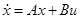 матрица A уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B, составленная из коэффициентов при управляющих параметрах.

С этой целью положим

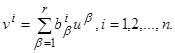                                                            (2.14)

Это означает, что вместо r управляющих параметров u¹,…,u^r вводятся n других управляющих параметров v¹,…, vⁿ, благодаря чему система (2.1) заменяется следующей:

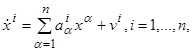
или в векторной форме,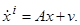

Нужно только выяснить, в каких пределах может изменяться точка v=(v¹, v²,…, vⁿ). Удобно считать, что эта точка v=(v¹, v²,…, vⁿ) расположена в том же пространстве X, что и точка x=(x¹,…, xⁿ).

Соотношения (2.14) определяют линейное отображение r-мерного пространства переменных u¹,…,u^r в фазовое пространство X. Образом многогранника U при отображении (2.14) является некоторый выпуклый многогранник в пространстве X, который мы обозначим через V.

Таким образом, получаем два линейных уравнения:

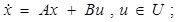                                                           (2.15)

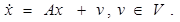                                                           (2.16)

Г л а в а III