Роль задач.

Под задачей будем понимать объект мыслительной деятельности,

содержащий требования и некоторые условия, в которых необходимо эти требования выполнить. Задачи, которые используют в процессе обучения математике, называют учебными математическими задачами.

Задачи в процессе обучения математике играют двоякую роль. С одной стороны, задачи – цель обучения математике. Качество математической подготовки учащегося оценивается с помощью задач, которые он способен решить на экзамене. С другой стороны, задачи служат средством обучения математике. Поэтому говорят, что задачи играют обучающую роль. Можно выделить несколько видов задач по их обучающей роли:

· задачи для усвоения математических понятий;

· задачи для обучения доказательствам;

· задачи для овладения математической символикой;

· задачи для формирования умений и навыков;

· пропедевтические задачи (предваряющие изучение нового материала, создающие проблемную ситуацию) и другие.

  Вместе с тем задачи играют развивающую роль, так как процесс их решения способствует:

· развитию мыслительных умений (например, таких как умение анализировать заданную ситуацию, сопоставлять данные и искомые величины, решаемые задачи с раннее решёнными, конструировать простейшие математические модели, отбирать необходимую информацию, систематизируя и обобщая её, оформлять свои мысли, оценивать полученные результаты, исследовать особые случаи);

· развитию логики мышления, так как приучает к полноценной аргументации, к потребности рассмотрения всех частных случаев (полноте дизъюнкции), к логически правильному использованию союзов «и», «или», к чётким формулировкам;

· активизации мыслительной деятельности учащихся посредством решения задач, включающих элементы исследования, на доказательство, на отыскание ошибок, занимательных, составленных самостоятельно.

  Приведём пример задачи, играющей развивающую роль: «через данную точку А проведите прямую, проходящую через лежащую вне чертежа току пересечения прямых а и b

Идея решения состоит в том, чтобы построить параллелограмм с вершиной в точке А и сторонами а₁ и b ₁ , параллельными данным прямым a и b , разделить его диагональ пополам и провести искомую прямую АО.

  Изменим условие задачи. Пусть точка пересечения прямых а и b ₁ «не помещается» на чертеже. Как в этом случае решить задачу?

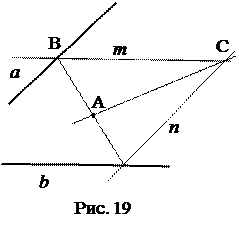
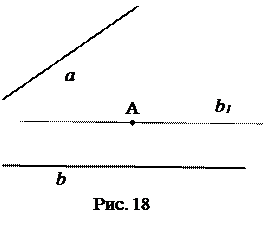
 Теперь идея решения задачи состоит в том, чтобы построить параллелограмм со сторонами на прямых а и b , как фигуру ценрально-симметричную относительно точки А. Для этого достаточно построить прямые т и п, центрально симметричные прямым а и b относительно точки А, и найти их точку пересечения С. Тогда СА – искомая прямая.

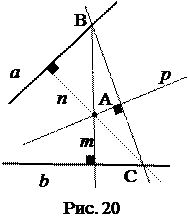Продолжим изменять условие задачи:  потребуем, чтобы искомая прямая была построена только с помощью прямоугольного чертёжного треугольника. Чтобы решить задачу с таким условием, будем считать точку А точкой пересечения высот некоторого треугольника со сторонами, принадлежащими прямым а и b. Через точку А проведем прямую, перпендикулярную к прямой а и продолжим её до пересечения с прямой b. Получим точку С (вершину треугольника). Аналогично получим точку В. ВС – сторона треугольника. Из точки А проведём перпендикуляр р к прямой ВС. Это и будет искомая прямая.

  Ясно, что процесс изменения условия задачи можно продолжить.

  Развивающую роль играют задачи, включающие элементы исследования, на доказательство, занимательные, на нахождение ошибок, на поиск  различных вариантов решения и выбор лучшего из них. Целесообразно составление задач учащимися.

  Задачи играют воспитывающую роль. Задача может воспитывать своей фабулой (текстовым содержанием). Например, подборка приведённая ниже  задач по арифметике из сборника С.А. Пономарёва и Н.И. Сырнева иллюстрирует возможности воспитания гражданина своей страны, гордящегося её природными богатствами,  успехами и достижениями.

№ 156. 7 мая 1895 года А.С. Попов демонстрировал первый в мире радиоприёмник. За 332 года 8 дней до этого начал печатать первые в России книги Иван Фёдоров. Когда начал печатать книги Иван Фёдоров?

№155 (1)

Первый советский искусственный спутник Земли был запущен 4 октября 1957 года, а прекратил своё существование 3 января 1958 года. Сколько времени находился в полёте первый советский искусственный спутник Земли?

№ 71. Высота кремлёвского холма 30 м, а Ленинских гор 78 м над уровнем Москвы-реки. Самое высокое здание на кремлёвском холме, колокольня Ивана Великого, имеет высоту 80 м и построено в 1600 году. Самое высокое здание на Ленинских горах, Московский университет, имеет высоту 240 м и построено в 1953 году. Составьте несколько задач по приведённым данным.

№ 779 (1). Длина Суэцкого канала 165,8 км, длина Панамского канала меньше Суэцкого на 84,7 км, а длина Беломорско – Балтийского канала на 145,9 км больше длины Панамского. Какова длина Беломорско – Балтийского канала?

№ 1075 (2). Ниже приведены длины важнейших рек Сибири: Обь с Иртышом 5206 км, Амур с Аргунью 4478 км, Лена 4264 км, Енисей 3807 км. Приняв длину Оби с Иртышом за 100%, выразите в процентах длины остальных рек (с точностью до 0,1%).

№ 1170 (2). Когда в самом западном пункте СССР (Калининградская область) полночь,  то  в  самом  восточном  пункте  СССР (мыс Дежнева) уже

11 час. 20 мин. На сколько градусов с востока на запад простирается территория СССР?

  Процесс решения задачи формирует настойчивость в достижении результата, аккуратность в записях (небрежно написанный знак минуса может и «отомстить»), вырабатывает трудолюбие, усидчивость, внимательность, сосредоточенность. «Нигде, как в математике, ясность и точность вывода не позволяет человеку отвертеться от ответа разговорами вокруг вопроса» писал известный советский математик А.Д. Александров. И в этом смысле работа с задачами воспитывает честность. Несомненно, что посредством решения математических задач формируется личность учащегося.

Место задач.

  Говоря о месте задач в обучении математике, следует ответить на вопрос «Где в учебном процессе они могут быть использованы?»

   1. Задачи могут быть полезны как средство мотивации изучения нового материала. Например, учащимся можно предложить вычислить значение выражения (50-0,3)² без калькулятора. Им придётся возводить 49,7 в квадрат. Естественно, записывая вычисления в столбик. Учитель может посчитать устно, так как знает формулу (а–в)²=а²-2ав+в²: 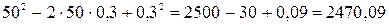 и тем самым мотивировать изучение формулы.

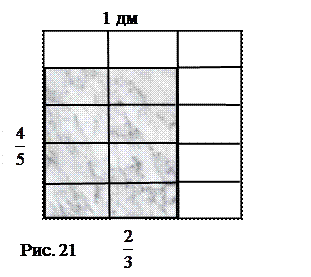   2. Задачи могут быть задействованы при объяснении нового материала (формировании понятия, изучении алгоритма). Например, убедить школьников в справедливости правила умножения обыкновенных дробей можно посредством задачи. Длина прямоугольника  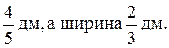Чему равна площадь прямоугольника? Изобразим данный прямоугольник.

        Рассматривая рисунок, получим 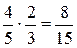. Как может быть получен такой результат?

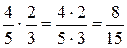. Посредством рассмотренной задачи может быть введён алгоритм.               

    3. Задачи могут быть использованы для закрепления изученного материала. Так, для закрепления понятия арифметического квадратного корня и его символа 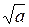 учащимся предлагаются следующие задачи.

№1. Назовите квадратные корни из 25; 0,04; 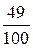 и укажите, какой из них является арифметическим.

№2. Докажите, что

1) число 9 есть арифметический квадратный корень из 81;

2) число -8 не является арифметическим квадратным корнем из 64;

3) число 0,3 не является арифметическим квадратным корнем из 0,9.

№3.

Прочитайте и докажите равенство:

1)

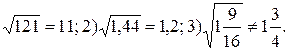
№4.

Найдите значение выражения:

1)

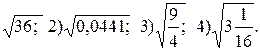
№5.

Найдите значение выражения:

1)

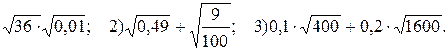
  4. Посредством задач можно проиллюстрировать приложения изученного материала. Например, приложения понятия «синус угла» в прямоугольном треугольнике можно показать с помощью задачи: «Угол подъёма дороги составляет в среднем 2°. На какую высоту поднимется турист, пройдя по дороге 12 км?»

  5. Задачи широко используются для формирования умений и навыков. В большом количестве такие задачи приводятся при изучении алгоритмов действий с натуральными, рациональными, положительными и отрицательными числами, выполнении тождественных преобразований выражений в алгебре. В геометрии такие задачи решаются при изучении преобразований фигур, решении основных задач на построение.

  6. Задачи используются при повторения учебного материала и его систематизации за счёт установления взаимосвязей между различными разделами, темами. Приведём пример такой задачи. «Найдите все значения параметра а, при которых действительные корни х₁, х₂ уравнения 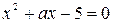удовлетворяют неравенству .

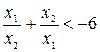Решение этой задачи предполагает:

· знание условия, при котором квадратное уравнение имеет действительные корни, теоремы Виета;  

· умение решать квадратное неравенство, умение складывать дроби, выражать сумму квадратов через сумму и произведение; решать дробно- рациональное неравенство методом интервалов.

  7. Задачи широко применяются как средство контроля качества математической подготовки учащихся. Контрольно - измерительные материалы ЕГЭ состоят из задач.

  8. Заниматься подготовкой к изучению понятия или темы также можно посредством задач. Например,  задание «Вычислите значения алгебраического выражения 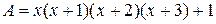 при заданных в таблице значениях переменной.                                                                                                                                             

Сколько значений А получено для каждого значения переменной х?» можно рассматривать как пропедевтическое для формирования понятия функции.

  Таким образом, задачи могут быть использованы на любом этапе процесса обучения математике.

  Анализ процесса решения задачи позволяет выделить в нём умственные действия и их взаимосвязи, представленные на следующей схеме.