Лекции по методике обучения математике

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекции по методике обучения математике

Общая методика

Составитель: кандидат педагогических наук,

доцент кафедры информатики и

методики преподавания математики

Бондаренко Татьяна Евгеньевна

Воронеж

ВГПУ

2014

Содержание

1. Предмет методики обучения математике . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

2. Цели обучения математике в школе . . . . . . . . . . . . . . . . . . . . . . . . . . 3

3. Лекции по общей методике обучения математике . . . . . . . . . . . . . . . . . . . 5

3.1. Математические понятия и методика их формирования . . . . . . . . . . . . . . 5

3.2.Теоремы и методика их изучения в курсе геометрии средней школы. . . 17

3.3. Задачи в процессе обучения математике. . . . . . . . . . . . . . . . . . . . . . . . . . 29

3.4. Методы обучения математике . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

Предмет методики обучения математике

Методика обучения математике (дидактика математики, педагогика математики, теория и методика обучения математике) – наука о математике как учебном предмете и закономерностях процесса обучения математике учащихся различных возрастных групп.

МОМ призвана ответить на следующие три вопроса:

1. Зачем следует обучать математике?

2. Что надо изучать?

3. Как надо обучать?

Таким образом, МОМ имеет своим предметом установление целей, определение содержания, разработку методов и организационных форм обучения.

Содержание МОМ составляют вопросы её общих теоретических основ (общая методика), а также вопросы изучения отдельных разделов и тем курса (частная или специальная МОМ)

МОМ тесно связана с другими науками: с математикой и её историей, с философией (теорией познания), психологией и возрастной физиологией, педагогикой (дидактикой). Учитывает богатый исторический опыт обучения математике и опыт передовых учителей.

Цели обучения математике

Один из возможных вариантов определения целей обучения математике представлен на следующей схеме:

Мировоззренческие цели направлены на создание условий для формирования математической составляющей целостной картины мира. Их можно разделить на информативные, практические и воспитательные.

Информативные цели связаны с усвоением учащимися системы математических знаний, идей и методов, с формированием умений и навыков.

Практические цели связаны с овладением учащимися методом математического моделирования, с умениями применять полученные знания на практике, в других учебных предметах, технике, пользоваться математическими инструментами, таблицами, схемами.

Воспитательные цели направлены на создание условий для развития устойчивого интереса к познанию, к изучению математики, на формирование таких качеств личности как воля, настойчивость, инициатива, активность и других.

Развивающие цели связаны с тем, что математика, как учебный предмет, обладает несравненными возможностями в развитии мышления человека. Обучение математике способствует развитию понятийного, логического, операционного, пространственного, алгоритмического, системного, критического мышления.

Общая методика обучения математике

Виды определений в школьном курсе математики

Структура определений

Наиболее часто встречаются определения конъюнктивной и дизъюнктивной структуры.

Если характеристические свойства определяемого понятия соединены союзом «и», то структура определения – конъюнктивная, если союзом «или», то дизъюнктивная.

Например, определение наибольшего общего делителя чисел а и в: «число с называется наибольшим общим делителем чисел а и в, если а делится на с и в делится на с и любой общий делитель чисел а и в делится на с» конъюнктивной структуры. Определение целых чисел: «числа натуральные, или им противоположные, или нуль называются целыми числами» - дизъюнктивной структуры.

Существуют определения и других структур, иногда более сложных. Например, определение предела функции в точке. Некоторые определения имеют условную структуру: «если а≠0, то а⁰=1».Посредством определения раскрывается содержание понятия. Вместе с тем, определение служит средством распознавания объектов, принадлежащих объёму понятия.

Распознавание объекта (явления) по определению понятия – это умственное действие, состоящее в проверке у имеющегося объекта (явления)

наличия тех характеристических свойств, которые указаны в определении. Результатом распознавания является вывод о принадлежности объекта объёму понятия. Отметим, что педагогике вместо термина «распознавание» используется термин «подведение под понятие».

Вывод о принадлежности или о непринадлежности объекта объёму понятия существенно зависит от структуры определения.

Если структура конъюнктивная, то объект принадлежит объёму понятия, если ему присуще каждое характеристическое свойство, указанное в определении; если дизъюнктивная, – то хотя бы одно из этих свойств.

Например, распознать среди данных на рисунке геометрических фигур четырёхугольники – это значит проверить наличие или отсутствие характеристических свойств, приведенных в определении четырёхугольника и сделать вывод, является ли данная фигура четырёхугольником.

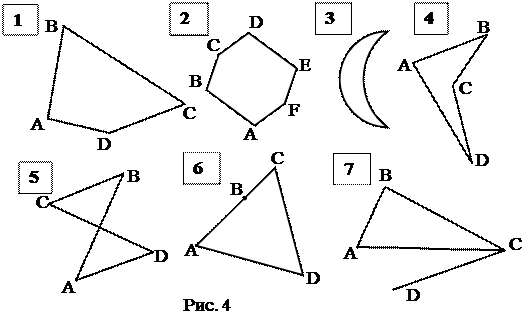
Приведём определение из учебника геометрии А.В. Погорелова для 7-9 классов: «четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться». Так как структура определения конъюнктивная, то рассматриваемая фигура является четырёхугольником, если ей присуще каждое характеристическое свойство, указанное в определении.

Ответить на вопрос, какие из чисел -3,5; 101, 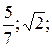-18; 0 являются целыми – это значит проверить (распознать), какие из них – натуральные, им противоположные или 0. Причём число будет целым, если ему присуще хотя бы одно характеристическое свойство из определения, так как его структура дизъюнктивная.

Требования, предъявляемые к определениям

1.Отсутствие порочного круга. Порочный круг предполагает, что определяемое понятие явно или неявно содержится в определяющем.

Контрпримеры.

1) Решение уравнения – это число, которое является его решением.

2) Угол называется прямым, если его стороны взаимно перпендикулярны. Две прямые называются взаимно перпендикулярными, если они образуют прямой угол.

2. Отсутствие омонимии: каждый термин должен встречаться не более одного раза в качестве определяемого, то есть один термин не должен обозначать разные понятия.

Контрпримеры.

1) Корень уравнения и корень из числа.

2) Квадрат – геометрическая фигура и произведение числа самого на себя.

3) Отношение двух чисел и бинарное отношение (параллельность, делимость).

Выбор ближайшего рода.

Контрпример.

1) Параллелограммом называется многоугольник, у которого противолежащие стороны попарно параллельны.

4. Достаточность. Определение должно содержать все существенные свойства понятия.

Контрпримеры.

1) Прямые называются параллельными, если они не пересекаются.

2) Смежными называются углы, имеющие общую сторону.

3) Произведение чисел, переменных или их степеней называется одночленом.

Отсутствие избыточности.

Контрпример.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Следует отметить, что в школьном курсе математики такие определения приводятся, исходя из методических соображений.

Средства для их реализации

Система целесообразно составленных вопросов и заданий для повторения необходимого материала.

Убедительные жизненные примеры, иллюстрирующие необходимость изучения нового понятия; проблемная ситуация, разрешение которой основано на использовании нового понятия.

3. Выделение существенных свойств понятия.

Цель: создание образов, адекватных формируемому понятию.

4. Синтез выделенных свойств, формулировка определения понятия

Цель: введение определения.

5. Работа над определением.

Цель: усвоение определения понятия

5.1. Усвоение формулировки

5.2. Анализ логический структуры определения.

5.3 Распознавание объектов по определению.

6. Изучение следствий из определения понятия (его свойств).

Цель: формирование понятия.

Примеры разнообразных моделей, обладающих такими свойствами.

Упражнения на построение объектов, удовлетворяющих указанным свойствам.

Упражнения на заполнение пропусков в формулировке определения, на нахождение ошибок в некорректных определениях.

Упражнения, способствующие выявлению логической структуры определения.

Упражнения на распознавание объектов, принадлежащих объёму понятия.

Учебные задачи на применение изученных свойств.

7. Изучение признаков понятия.

Цель: формирование понятия.

Учебные задачи на применение изученных признаков, в том числе на переформулировку определения понятия.

8. Установление связей изученного

понятия с другими понятиями.

Конструирование родословной понятия; его включение в существующую классификацию,

например, с помощью кругов Эйлера; задачи, в которых понятие используется в связи

с ранее изученными.

Формирование понятия дедуктивным методом осуществляется по следующему плану:

1. Формулировка определения нового понятия.

2. Рассмотрение частных и особых случаев выражения этого понятия.

3. Иллюстрация введённого понятия на конкретных примерах.

4. Изучение свойств и признаков понятия.

5. Аспекты применения понятия.

Отметим, что индуктивный метод применяется в старших классах, в

вузовской практике, а индуктивный – чаще используется в младших и средних классах.

Литература

1. Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н.Л. Стефановой. – М., Дрофа, 2005.

2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев, - М.: Просвещение, 2002.

3. Методика преподавания математики в средней школе: общая методика, Учеб. пособие для студентов пед. ин-тов / составители Р. С. Черкасов, А. А. Столяр. – М., Просвещение, 1985.

Теоремы и их виды

Связь между понятиями устанавливается с помощью суждений. Суждением принято называть предложение, в котором выражается мысль о предмете, объекте, явлении. Существуют два основных свойства суждения: что-то утверждать или отрицать, быть истинным или ложным.

Выделяются следующие виды суждений:

· общеутвердительное (образуется с помощью кванторных слов: всякий, любой);

· частно утвердительное (образуется с помощью кванторных слов: существуют, некоторые);

· общеотрицательное (образуется с помощью кванторных слов: ни один, никакой, не существует);

· частно отрицательное (образуется с помощью кванторных слов: не всякий, не любой).

Часто кванторные слова опускаются, считается, что они понятны из смысла всего предложения.

Например,

«все квадраты суть прямоугольники» - общеутвердительное суждение; «некоторые треугольники равнобедренные» - частно утвердительное суждение;

«не существует рационального числа, квадрат которого равен 2» - общеотрицательное суждение;

«не любое натуральное число – чётное» - частно отрицательное суждение.

Математическим предложением называют повествовательное предложение, выражающее общеутвердительное или общеотрицательное суждение о математических объектах.

Под теоремой принято понимать математическое предложение (утверждение), истинность которого доказывается.

Таким образом, родословную понятия «теорема» можно охарактеризовать «цепочкой» понятий: теорема→математическое предложение→ суждение.

Запись теоремы состоит из формулировки (суждения, утверждения) и доказательства.

Виды формулировки теоремы

Формулировка теоремы может быть категорической или условной. Для условной формы характерны слова «если…, то…». Например, «если в параллелограмме диагонали равны, то параллелограмм является прямоугольником». Теорема «сумма углов треугольника равна 180°» сформулирована в категорической форме.

В формулировке каждой теоремы можно выделить условие (то, что дано) и заключение (то, что требуется доказать). Если теорема сформулирована в условной форме, то между словами «если…, то» содержится её условие, после слова «то» - заключение. Пусть Р – условие теоремы, а Q – её заключение. Тогда символически теорему можно записать в виде Р Þ Q (если Р, то Q). При выделении условия и заключения в теореме, сформулированной в категорической форме, нет такой ясности. Поэтому целесообразно научить школьников переходить от условной к категорической формулировке теоремы. Так, приведённую выше теорему можно переформулировать: «если данная фигура – треугольник, то сумма его углов равна 180°».

Из данной теоремы (1) могут быть образованы ещё три утверждения. Поменяем местами условие и заключение. Получим обратное утверждение (2) Q Þ Р (если Q, то Р). Оно может быть истинным (тогда это обратная теорема) или ложным. Заменим условие и заключение теоремы на их отрицание. Получим противоположное утверждение (3) 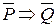(если не Р, то не Q). Оно также может быть либо истинным (теоремой), либо ложным. Наконец, может быть составлено контрапозитивное утверждение вида (4) .

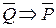Например, из теоремы «если углы вертикальны (Р), то они равны (Q)» (1) можно образовать следующие утверждения:

«если углы равны (Q), то они вертикальны (Р)» (2);

«если углы не вертикальны ( 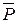), то они не равны ( 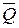)» (3);

«если углы не равны ( 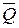),то они не вертикальны ( 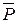)» (4).

Утверждения (1) и (4) истинны, а (2) и (3) – ложны. В математической логике доказывается, что утверждения (1) и (4), (2) и (3) равносильны, то есть их таблицы истинности совпадают. Схематически это можно изобразить так:

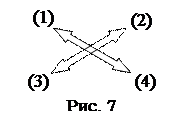
Аналогичным примером из алгебры является теорема «если каждое слагаемое делится на число, то и сумма делится на это число». Теорема «если в четырёхугольнике суммы противоположных сторон равны, то в него можно вписать окружность» служит примером истинности всех четырех утверждений.

Необходимое и достаточное условия

Пусть теорема сформулирована в виде Р Þ Q (если Р, то Q). Тогда Q называют необходимым условием Р, а Р – достаточным условием Q. Ясно, что Q – необходимое и достаточное условие Р, если обратное утверждение является истинным. Например, равенство углов является необходимым условием их вертикальности, а вертикальность углов является достаточным условием их равенства. При этом равенство углов не является необходимым и достаточным условием их вертикальности, так как обратное утверждение не является истинным. Равенство сумм противоположных углов четырёхугольника является необходимым и достаточным условием того, что в него можно вписать окружность. Подчёркивая этот факт, теорему формулируют в виде «для того, чтобы в четырёхугольник можно было вписать окружность необходимо и достаточно, чтобы суммы его противоположных сторон были равны». При этом доказывается истинность необходимого и достаточного условий. Доказывая необходимость, следует выделенное условие поставить в заключение теоремы.

Необходимость.

Дано: четырёхугольник; окружность, вписанная в четырёхугольник.

Доказать: суммы противоположных сторон четырёхугольника равны.

Затем докажем истинность обратной теоремы и тем самым докажем достаточность.

Достаточность.

Дано: суммы противоположных сторон четырёхугольника равны.

Доказать: в четырёхугольник можно вписать окружность.

Если некоторое условие Q является необходимым и достаточным условием Р, то его называют критерием Р. Так, равенство сумм противоположных сторон четырёхугольника является критерием того, что в него можно вписать окружность.

Доказательство теоремы

Процесс доказательства является предметом изучения логики, Мы рассмотрим некоторые аспекты, относящиеся к доказательству теорем в школе.

Одним из основных элементов доказательства теорем является умозаключение. Умозаключение есть мыслительная операция, в результате которой из одного или нескольких суждений, находящихся в определённой смысловой взаимной связи, получается новое суждение. По отношению к исходным суждением оно содержит новое знание. Исходные суждения – это посылки, полученное новое суждение – это вывод.

При доказательстве теорем в школьном курсе математики наиболее часто используется умозаключение, называемое силлогизмом. Оно имеет следующее строение:

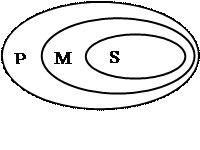
Все М суть Р (большая посылка)

Все S суть М (малая посылка)

S суть Р (вывод)

Рис. 8

Доказательство теоремы – это цепочка последовательно связанных силлогизмов, устанавливающих её истинность. При этом посылками силлогизмов могут быть аксиомы, теоремы, определения.

В качестве примера рассмотрим доказательство теоремы: «при пересечении двух параллельных прямых секущей соответственные углы равны».

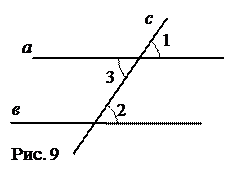
Дано: а || b. c – секущая,

Доказать: Ð1=Ð2.

1 силлогизм:

Б.П.: Вертикальные углы равны.

М.П.: Ð 1 и Ð 3 –вертикальные.

В.: Ð1 = Ð3

2 силлогизм:

Б.П.: При пересечении двух параллельных прямых третьей внутренние накрест лежащие углы равны.

М. П.: Ð 2 и Ð 3 – внутренние накрест лежащие.

В.: Ð2 = Ð3

3 силлогизм.

Б.П. Если правые части равенства равны, то равны и левые части.

М.П.: Ð1 = Ð3, Ð2 = Ð3.

В.: Ð1=Ð2.

Существуют и другие правила вывода, например, отрицания,

контрапозиции.

Все доказательства можно разделить на прямые и косвенные. При прямом доказательстве задача состоит в том, чтобы подыскать такие утверждения, из которых по правилам вывода прийти к заключению теоремы. Доказательство, которое основывается на установлении истинности посредством опровержения некоторых суждений, называется косвенным. К косвенным доказательствам относится метод доказательства от противного или разделительный метод. Описание названных методов рассмотрите по учебному пособию [2, стр. 82].

1.3.

В₁

Дано: DАВС и DА₁В₁С₁.

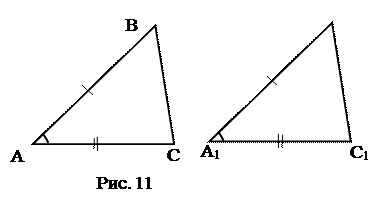
АВ = А₁В₁, АС =А₁С₁,

ÐА=ÐА₁.

Доказать: DАВС = DА₁В₁С₁.

2. По определению равенство треугольников предполагает наличие трёх пар равных элементов, признак сокращает их в 2 раза: до трёх пар равных элементов. Теорема играет важнейшую роль в курсе планиметрии, так как доказательство равенства треугольников станет основным методом доказательства.

3. Метод доказательства состоит в рассмотрении третьего треугольника

А₂В₂С₂, равного треугольнику АВС и совпадающего с треугольником А₁В₁С₁.

4.1. Самостоятельное доказательство теоремы учащимися в данном случае невозможно в связи с полным отсутствием опыта и сложностью метода доказательства.

4.2. Алгоритм доказательства:

1. Утверждаем существование треугольника А₂В₂С₂ равного треугольнику АВС и определённым образом расположенного относительно треугольника А₁В₁С₁.

2. Доказываем совпадение треугольников А₂В₂С₂ и А₁В₁С₁.

3. Делаем вывод о равенстве треугольников АВС и А₁В₁С₁

4.3. Доказательство

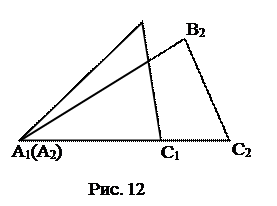
1) По аксиоме VIII существует D А₂В₂С₂= D АВС:

вершина А₂ совпадает с вершиной А₁;

вершина С₂принадлежит лучу А₁С₁;

вершина В₂ лежит в одной полуплоскости с вершиной В₁ относительно прямой А₁С₁.

В₁

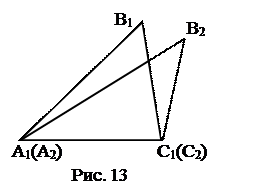
2) Докажем, что вершины С₁ и С₂ совпадают.

А₁С₁ = АС (по условию),

АС=А₂С₂(так как DА₂В₂С₂=DАВС).

---------------------------------------------------

А₁С₁=А₂С₂.

Следовательно, по аксиоме откладывания отрезков точки С₁ и С₂ совпадают.

Коррекция чертежа.

3) Докажем, что лучи А₁В₁ и А₂В₂ совпадают.

ÐА=ÐА₁(по условию),

ÐА=ÐА₂(так как DА₂В₂С₂=DАВС).

------------------------------------------------------

ÐА₁=ÐА₂.

Следовательно, по аксиоме откладывания углов лучи А₁В₁ и А₂В₂ совпадают.

Коррекция чертежа.

4) Докажем, что вершины В₁ и В₂ совпадают.

Доказательство аналогично пункту (1)

Коррекция чертежа.

5) Вывод. По аксиоме о о единственности прямой, проходящей через две точки, треугольники А₂В₂С₂ и А₁В₁С₁ совпали. По сути это два имени одного и того же треугольника. Так как DА₂В₂С₂=DАВС, то и А₁В₁С₁=DАВС. Что и требовалось доказать.

5. В доказательстве теоремы используется:

· аксиома откладывания отрезков (VI);

· аксиома откладывания углов (VII);

· определение равных треугольников.

· аксиома существования треугольника, равного данному (VIII);

· аксиома о единственности прямой, проходящей через две точки (I).

В соответствии с приведённым списком учащимся могут быть предложены следующие задания на актуализацию знаний.

№1. На полупрямой а от её начальной точки B отложили два равных отрезка BM и BK. Что можно сказать о точках М и К? Обоснуйте ответ.

№2. От полупрямой а в одну и ту же полуплоскость отложены два равных угла (ав) и (ас). Что можно сказать о лучах а и с? Обоснуйте ответ.

№3. Сформулируйте аксиому существования треугольника, равного данному.

№4. Что означает выражение «Треугольник DAK равен треугольнику MNB»?

№5. Сколько равенств отрезков и углов определяют равенство треугольников?

6. В данном случае математическая ситуация исследована. Другие случаи не рассматриваются.

7. Иные способы доказательства не рассматриваем.

8. Приведём примеры задач по готовым чертежам, способствующих усвоению первого признака равенства треугольников.

Найти пары равных треугольников и доказать их равенство.

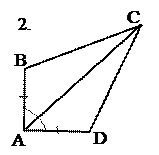
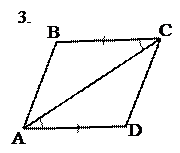
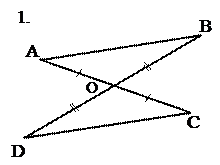
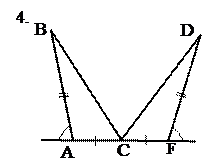
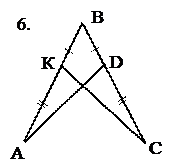
Рис. 16

Литература

4. Погорелов А.В. Геометрия. 7- 9 классы: учебник для общеобразоват. учреждений / А.В. Погорелов. - 13-е изд. – М.: Просвещение, 2012 г.

Роль задач.

Под задачей будем понимать объект мыслительной деятельности,

содержащий требования и некоторые условия, в которых необходимо эти требования выполнить. Задачи, которые используют в процессе обучения математике, называют учебными математическими задачами.

Задачи в процессе обучения математике играют двоякую роль. С одной стороны, задачи – цель обучения математике. Качество математической подготовки учащегося оценивается с помощью задач, которые он способен решить на экзамене. С другой стороны, задачи служат средством обучения математике. Поэтому говорят, что задачи играют обучающую роль. Можно выделить несколько видов задач по их обучающей роли:

· задачи для усвоения математических понятий;

· задачи для обучения доказательствам;

· задачи для овладения математической символикой;

· задачи для формирования умений и навыков;

· пропедевтические задачи (предваряющие изучение нового материала, создающие проблемную ситуацию) и другие.

Вместе с тем задачи играют развивающую роль, так как процесс их решения способствует:

· развитию мыслительных умений (например, таких как умение анализировать заданную ситуацию, сопоставлять данные и искомые величины, решаемые задачи с раннее решёнными, конструировать простейшие математические модели, отбирать необходимую информацию, систематизируя и обобщая её, оформлять свои мысли, оценивать полученные результаты, исследовать особые случаи);

· развитию логики мышления, так как приучает к полноценной аргументации, к потребности рассмотрения всех частных случаев (полноте дизъюнкции), к логически правильному использованию союзов «и», «или», к чётким формулировкам;

· активизации мыслительной деятельности учащихся посредством решения задач, включающих элементы исследования, на доказательство, на отыскание ошибок, занимательных, составленных самостоятельно.

Приведём пример задачи, играющей развивающую роль: «через данную точку А проведите прямую, проходящую через лежащую вне чертежа току пересечения прямых а и b

Идея решения состоит в том, чтобы построить параллелограмм с вершиной в точке А и сторонами а₁и b ₁ , параллельными данным прямым a и b , разделить его диагональ пополам и провести искомую прямую АО.

Изменим условие задачи. Пусть точка пересечения прямых а и b ₁ «не помещается» на чертеже. Как в этом случае решить задачу?

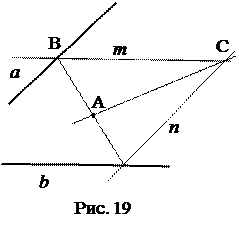
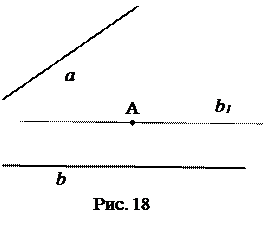
Теперь идея решения задачи состоит в том, чтобы построить параллелограмм со сторонами на прямых а и b , как фигуру ценрально-симметричную относительно точки А. Для этого достаточно построить прямые т и п, центрально симметричные прямым а и b относительно точки А, и найти их точку пересечения С. Тогда СА – искомая прямая.

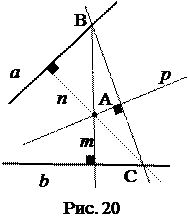Продолжим изменять условие задачи: потребуем, чтобы искомая прямая была построена только с помощью прямоугольного чертёжного треугольника. Чтобы решить задачу с таким условием, будем считать точку А точкой пересечения высот некоторого треугольника со сторонами, принадлежащими прямым а и b. Через точку А проведем прямую, перпендикулярную к прямой а и продолжим её до пересечения с прямой b. Получим точку С (вершину треугольника). Аналогично получим точку В. ВС – сторона треугольника. Из точки А проведём перпендикуляр р к прямой ВС. Это и будет искомая прямая.

Ясно, что процесс изменения условия задачи можно продолжить.

Развивающую роль играют задачи, включающие элементы исследования, на доказательство, занимательные, на нахождение ошибок, на поиск различных вариантов решения и выбор лучшего из них. Целесообразно составление задач учащимися.

Задачи играют воспитывающую роль. Задача может воспитывать своей фабулой (текстовым содержанием). Например, подборка приведённая ниже задач по арифметике из сборника С.А. Пономарёва и Н.И. Сырнева иллюстрирует возможности воспитания гражданина своей страны, гордящегося её природными богатствами, успехами и достижениями.

№ 156. 7 мая 1895 года А.С. Попов демонстрировал первый в мире радиоприёмник. За 332 года 8 дней до этого начал печатать первые в России книги Иван Фёдоров. Когда начал печатать книги Иван Фёдоров?

№155 (1)

Первый советский искусственный спутник Земли был запущен 4 октября 1957 года, а прекратил своё существование 3 января 1958 года. Сколько времени находился в полёте первый советский искусственный спутник Земли?

№ 71. Высота кремлёвского холма 30 м, а Ленинских гор 78 м над уровнем Москвы-реки. Самое высокое здание на кремлёвском холме, колокольня Ивана Великого, имеет высоту 80 м и построено в 1600 году. Самое высокое здание на Ленинских горах, Московский университет, имеет высоту 240 м и построено в 1953 году. Составьте несколько задач по приведённым данным.

№ 779 (1). Длина Суэцкого канала 165,8 км, длина Панамского канала меньше Суэцкого на 84,7 км, а длина Беломорско – Балтийского канала на 145,9 км больше длины Панамского. Какова длина Беломорско – Балтийского канала?

№ 1075 (2). Ниже приведены длины важнейших рек Сибири: Обь с Иртышом 5206 км, Амур с Аргунью 4478 км, Лена 4264 км, Енисей 3807 км. Приняв длину Оби с Иртышом за 100%, выразите в процентах длины остальных рек (с точностью до 0,1%).

№ 1170 (2). Когда в самом западном пункте СССР (Калининградская область) полночь, то в самом восточном пункте СССР (мыс Дежнева) уже

11 час. 20 мин. На сколько градусов с востока на запад простирается территория СССР?

Процесс решения задачи формирует настойчивость в достижении результата, аккуратность в записях (небрежно написанный знак минуса может и «отомстить»), вырабатывает трудолюбие, усидчивость, внимательность, сосредоточенность. «Нигде, как в математике, ясность и точность вывода не позволяет человеку отвертеться от ответа разговорами вокруг вопроса» писал известный советский математик А.Д. Александров. И в этом смысле работа с задачами воспитывает честность. Несомненно, что посредством решения математических задач формируется личность учащегося.

Место задач.

Говоря о месте задач в обучении математике, следует ответить на вопрос «Где в учебном процессе они могут быть использованы?»

1. Задачи могут быть полезны как средство мотивации изучения нового материала. Например, учащимся можно предложить вычислить значение выражения (50-0,3)²без калькулятора. Им придётся возводить 49,7 в квадрат. Естественно, записывая вычисления в столбик. Учитель может посчитать устно, так как знает формулу (а–в)²=а²-2ав+в²: 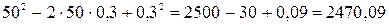и тем самым мотивировать изучение формулы.

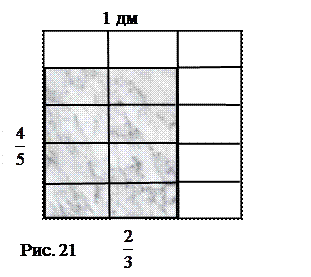2. Задачи могут быть задействованы при объяснении нового материала (формировании понятия, изучении алгоритма). Например, убедить школьников в справедливости правила умножения обыкновенных дробей можно посредством задачи. Длина прямоугольника 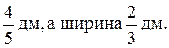Чему равна площадь прямоугольника? Изобразим данный прямоугольник.

Рассматривая рисунок, получим 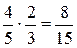. Как может быть получен такой результат?

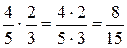. Посредством рассмотренной задачи может быть введён алгоритм.

3. Задачи могут быть использованы для закрепления изученного материала. Так, для закрепления понятия арифметического квадратного корня и его символа 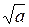учащимся предлагаются следующие задачи.

№1. Назовите квадратные корни из 25; 0,04; 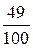и укажите, какой из них является арифметическим.

№2. Докажите, что

1) число 9 есть арифметический квадратный корень из 81;

2) число -8 не является арифметическим квадратным корнем из 64;

3) число 0,3 не является арифметическим квадратным корнем из 0,9.

№3.

Прочитайте и докажите равенство:

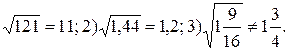
№4.

Найдите значение выражения:

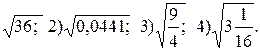
№5.

Найдите значение выражения:

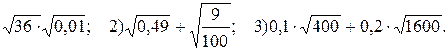
4. Посредством задач можно проиллюстрировать приложения изученного материала. Например, приложения понятия «синус угла» в прямоугольном треугольнике можно показать с помощью задачи: «Угол подъёма дороги составляет в среднем 2°. На какую высоту поднимется турист, пройдя по дороге 12 км?»

5. Задачи широко используются для формирования умений и навыков. В большом количестве такие задачи приводятся при изучении алгоритмов действий с натуральными, рациональными, положительными и отрицательными числами, выполнении тождественных преобразований выражений в алгебре. В геометрии такие задачи решаются при изучении преобразований фигур, решении основных задач на построение.

6. Задачи используются при повторения учебного материала и его систематизации за счёт установления взаимосвязей между различными разделами, темами. Приведём пример такой задачи. «Найдите все значения параметра а, при которых действительные корни х₁, х₂уравнения 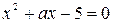удовлетворяют неравенству .

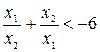Решение этой задачи предполагает:

· знание условия, при котором квадратное уравнение имеет действительные корни, теоремы Виета;

· умение решать квадратное неравенство, умение складывать дроби, выражать сумму квадратов через сумму и произведение; решать дробно- рациональное неравенство методом интервалов.

7. Задачи широко применяются как средство контроля качества математической подготовки учащихся. Контрольно - измерительные материалы ЕГЭ состоят из задач.

х	1	3	-4	1/2	-1,5
А

8. Заниматься подготовкой к изучению понятия или темы также можно посредством задач. Например, задание «Вычислите значения алгебраического выражения 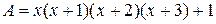при заданных в таблице значениях переменной.

Сколько значений А получено для каждого значения переменной х?» можно рассматривать как пропедевтическое для формирования понятия функции.

Таким образом, задачи могут быть использованы на любом этапе процесса обучения математике.

Анализ процесса решения задачи позволяет выделить в нём умственные действия и их взаимосвязи, представленные на следующей схеме.

Литература

Методы обучения математике

Под методами обучения будем понимать упорядоченные способы взаимосвязанной деятельности учителя и учащихся, направленные на достижение целей обучения.

Такой подход включает методы обучающей деятельности учителя (методы преподавания), методы познавательной деятельности ученика (методы изучения) и способы, посредством которых обучающая деятельность учителя управляет познавательной деятельностью ученика.

Под методами преподавания математики понимают способы передачи учащимся определённой системы математических знаний, умений и навыков.

К методам преподавания относятся лекция, рассказ, инструкция по работе с учебником, выполнению лабораторной или практической работы и другие. К методам преподавания следует обращаться тогда, когда учащиеся должны научиться действовать по «образцу» или в случае, когда они не способны усвоить материал самостоятельно. Например, нет подходящего источника изучения или он слишком сложен.

Под методами изучения математики понимают способы осуществления активной, самостоятельной деятельности математического характера самих школьников. Среди методов изучения математики условно выделяют научные и учебные методы.

К научным методам относятся:

· наблюдение и опыт (эксперимент);

· сравнение и аналогия;

· обобщение и абстрагирование;

· анализ и синтез;

· индукция и дедукция.

Перечисленные методы применяются в научных исследованиях, они служат средством приобретения новых знаний в науке. Естественно их использование в адаптированной (приспособленной) для этого форме в процессе познания учащегося.

Учебные методы изучения математики специально созданы в методике с целью эффективного изучения предмета. Назовём среди них эвристический метод, метод обучения на моделях, метод программированного обучения.

Представим приведённую классификацию методов схематически.

Отметим, что в практике обучения методы преподавания и изучения прочно взаимосвязаны, и разделить их не всегда удаётся. Остановимся более подробно на названных научных методах.

Наблюдение и опыт

Наблюдением называется метод изучения объектов и явлений окружающего мира в их естественных условиях. Под опытом (экспериментом) понимают такой метод изучения предметов и явлений, который предполагает вмешательство в их естественное состояние, создание искусственных условий, разделение на части, соединение с другими объектами и явлениями. Всякий опыт связан с наблюдением. Они должны быть направлены на создание специальных ситуаций, чтобы предоставить учащимся возможность выявить очевидные закономерности, факты, идеи доказательства.

Например, наблюдая чертежи, можно согласиться с разумностью следующих утверждений:

· через любые две различные точки плоскости проходит единственная прямая;

· прямая делит плоскость на две полуплоскости;

· если две различные точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости;

· простые числа в ряду натуральных чисел распределены неравномерно;

· если дискриминант квадратного трёхчлена 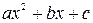отрицателен, то функция 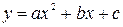принимает постоянные по знаку значения.

С помощью опыта, состоящего в разрезании треугольника, можно

показать учащимся, что сумма углов треугольника равна 180°

Если на листе бумаги провести прямую линию, нанести цветную капельку, перегнуть лист по начерченной прямой и прогладить рукой половинки, то развернув лист, можно наблюдать фигуры, симметричные относительно прямой. С помощью прибора, изобретённого в 1603 году Христофором Шейнером, и названного пантографом, можно наблюдать подобные фигуры.

Названные методы помогают самостоятельному открытию учащимися математических фактов, они служат эвристическим средством. Особую роль эти методы играют в младших классах. К недостаткам их следует отнести то, что ни один из них не является средством доказательства.

Сравнение и аналогия

Сравнение математических фигур и величин

служит материалом для игр и обучения мудрости

Песталоцци И.Г.

В дидактике сравнение должно быть основным

приёмом

Ушинский К.Д.

Сравнение – мысленное установление сходств и различий объектов изучения. Например, сравнение параллелограмма и трапеции позволяет выделить их общие свойства: они оба четырёхугольники, оба имеют параллельные стороны, - и различие: в одном две пары параллельных сторон, в другом – одна. Сравнение обыкновенных и алгебраических дробей выявляет их сходство: наличие числителя и знаменателя, отсутствие значения, когда знаменатель обращается в нуль и различие: в одном случае числитель и знаменатель – числа, в другом алгебраические выражения.

Сравнение как метод исследования широко применяется в математике не только для изучения математических свойств объекта, но и для установления самих этих свойств. В этом смысле особую роль играет аналогия – сравнение

по сходству. Рассуждение по аналогии состоит в следующем: если два предмета или явления имеют какие–то общие признаки, то, вероятно, они могут иметь и другие общие признаки.

Схематически:

Объёкт А имеет признаки а, в, с ,х.

Объёкт В имеет признаки а, в, с.

Заключение по аналогии: вероятно объект В имеет признак х.

Заключение по аналогии следует доказать или опровергнуть.

Рассмотрим примеры рассуждений по аналогии.

По теореме Пифагора квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах. Все квадраты подобны. Построим подобные многоугольники ( на рисунке подобные треугольники) на гипотенузе и катетах так, чтобы сходственными сторонами этих многоугольников служили стороны треугольника.

Сформулируем утверждение, аналогичное теореме Пифагора: многоугольник, построенный на гипотенузе равновелик сумме подобных многоугольников, построенных на катетах. Дополнительные исследования показывают, что это верно. Распространим приведённую аналогию на кубы с ребрами, равными гипотенузе и катетам данного прямоугольного треугольника. Аналогичное утверждение о равновеликости куба, построенного на гипотенузе и суммы кубов, построенных на катетах, оказывается неверным: пусть с – гипотенуза треугольника, а и в – его катеты, тогда с>а, | a²

+ с>в; | b²

ca²+c b²> a³+ b³, c(a²+ b²) > a³+ b³, c³> a³+ b³.

Аналогия имеет широкое применение в в процессе обучения математике. Приведём пример. Параллелепипед – пространственный аналог параллелограмма. В параллелограмме противоположные стороны параллельны, в параллелепипеде противоположные грани параллельны. Рассуждая по аналогии, можно прийти к гипотезе, что в параллелепипеде также как и в параллелограмме, диагонали, пересекаясь, делятся точкой пересечения пополам. Но если видеть только сходство и не замечать различия, в частности, что в параллелограмме всего две диагонали, а в параллелепипеде - четыре, то мы упустим важное свойство, подлежащее доказательству: все диагонали параллелепипеда пересекаются в одной точке.

Следовательно, применению аналогии должно предшествовать сравнение, с помощью которого выделяется как сходство, так и различие.

Используя аналогию, в школе изучают натуральные числа и десятичные дроби, обыкновенные и алгебраические дроби, сферу и окружность, круг и шар . . . Иногда аналогия оказывает «медвежью услугу» Так, по аналогии с верным свойством арифметических корней 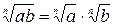учащиеся используют свойство 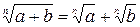, в неверности которого их можно убедить, например, для а = 9, в = 16. Такие примеры «вредных» аналогий можно продолжить. Однако полезность аналогий позволяла великому немецкому математику и астроному Иоганну Кеплеру писать: «И я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и им меньше всего следует пренебрегать в Геометрии».

Обобщение и абстрагирование

Обобщение и абстрагирование - два логических приёма, применяемых почти всегда совместно в процессе познания.

Обобщение – мысленное выделение, фиксирование каких либо общих существенных свойств, принадлежащих данному классу объектов или отношений. Абстрагирование - мысленное отвлечение, отделение общих существенных свойств, выделенных в результате обобщения, от прочих несущественных или необщих свойств рассматриваемых предметов или отношений и отбрасывание (в рамках нашего изучения) последних.

Обобщение и абстрагирование применяются как эвристическое средство и как средство введения нового понятия. Приведём примеры.

1. В математике понятие производной вводится посредством двух задач: о скорости и о касательной. Обобщая процесс решения этих задач приходим к выводу, что в каждом случае мы действовали по одному и тому же общему алгоритму: придавали приращение аргументу, находили соответствующее приращение функции, затем вычисляли отношение этих приращений и его предел. Абстрагируясь от конкретного содержания задач, вводим понятие производной

2. В школе проиллюстрируем применение этих методов при изучении распределительного закона умножения относительно сложения в 5 классе.

Учащимся предлагаются следующие задачи.

№1. В школьном саду посажены фруктовые деревья в 8 рядов. В каждом ряду посажено по 7яблонь и 5 груш. Сколько всего деревьев посажено в саду?

Решение.

1 способ. 7+ 5деревьев посажено в каждом ряду, а всего (7+5)×8 деревьев;

2 способ. 7×8 яблонь было посажен в саду, 5×8 – груш, а всего 7×8+5×8 деревьев.

По смыслу задачи ясно, что справедливо равенство (7+5)×8=7×8+5×8.

Ответ: 96 деревьев.

№2. Автобус и автомобиль одновременно выехали навстречу друг другу из двух пунктов. Скорость автобуса 60 км/ч, а автомобиля 80 км/ч. Через три часа они встретились. Каково расстояние между пунктами?

1 способ. Скорость сближения автобуса и автомобиля (60+80) км/ч, за 3 часа они сблизятся на (60+80)×3 км.

2 способ. Автобус до встречи пройдёт 60×3 км, а автомобиль 80×3 км. Расстояние между пунктами составит (60×3 + 80×3) км.

По смыслу задачи ясно, что справедливо равенство (60+80)×3=60×3+80×3.

Ответ: 420 км.

№3. Найти общую площадь двух участков прямоугольной формы, изображённых на рисунке.

1 способ. Решая задачу, можно составить выражение (5+3) ×4 (кв.м).

2 способ. Решая задачу, можно составить выражение 5×4+3×4 (кв.м).

По смыслу задачи ясно, что справедливо равенство (5+3) ×4=5×4+3×4.

Ответ: 32 кв.м.

Обобщая решения задач и абстрагируясь от их конкретного содержания, приходим к выводу, что для того, чтобы умножить сумму двух чисел на третье число, можно каждое слагаемое умножить на это число и полученные произведения сложить. Запишем этот закон с помощью переменных:

(а + b ) × с =а × с + b × с

и назовём его распределительным законом умножения относительно сложения.

Обобщение и абстрагирование могу использоваться при решении задач.

Рассмотрим задачу: для того, чтобы выяснить, сколько рыб в пруду, взяли сеть с заранее выбранным размером ячеек и, вытащив её, обнаружили 30 рыб. Отметили каждую меткой и бросили обратно в пруд. На другой день забросили эту же сеть и поймали 40 рыб, причём среди них две меченные. Сколько рыб в пруду, годных для улова?

Решение. Так как меченные рыбы составляют 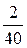или 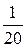всех рыб, а всего их 30, то рыб в пруду не менее 20×30=600.

Обобщая существенные данные задачи и абстрагируясь от её конкретного содержания, сформулируем общую задачу: имеется урна с шарами. Из неё извлекается k шаров и делается пометка. Шары возвращаются в урну и перемешиваются. После этого извлекается п шаров и обнаруживается, что среди них т меченых шаров (т£п). Сколько шаров в урне?

Решая по аналогии с задачей о рыбах, получим, что меченые шары составляют 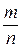часть или k шаров. Следовательно, шаров в урне .

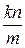Анализ и синтез

Анализ и синтез могут рассматриваться в двух формах:

1) анализ - логический приём, состоящий в том, что изучаемый предмет мысленно разбивается на части, каждая из которых затем исследуется отдельно, а синтез как обратная операция восстановления целого (анализ в форме расчленения);

2) анализ - метод рассуждений от искомых к данным задачи, а синтез -от данных к искомым (анализ в форме рассуждения).

Общая схема анализа в форме расчленения:

· разбиваем условие задачи на отдельные части;

· выделяем некоторые условия (остальные пока не учитываются);

· из отобранных условий составляем более лёгкую вспомогательную задачу и решаем её;

· дополняем отброшенные условия и переходим к решению данной задачи.

Примеры.

№1. Сократить дробь .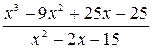

Естественно разбить данную дробь на числитель и знаменатель. Знаменатель тривиально раскладывается на множители 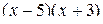. Проверим, какие из нулей знаменателя х=5 или х= -3 являются нулями числителя. Убеждаемся, что это х=5. Выделяем в числителе множитель х-5: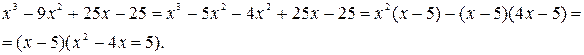

В результате получаем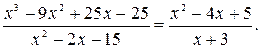

№2. Построить треугольник по отношению т : п двух сторон, углу между ними и высоте проведенной к третьей стороне.

Вычленим условие: построить треугольник по отношению т : п двух сторон, углу между ними. Треугольник со сторонами т и п и с углом между ними, равным данному удовлетворяет выделенным условиям. Построим его.

Подключаем данную по условию высоту, проведённую к третьей стороне. Построим её в полученном треугольнике.

Достроим полученную конфигурацию до искомого треугольника.

DМАС – искомый.

Такой приём решения задач иногда называю разбиением на подзадачи.

Примером анализа в форме расчленения является исследование функции по известному плану, а синтеза – построение её графика на основе полученных в процессе анализа свойств.

Анализ в форме рассуждений делится на нисходящий и восходящий.

Нисходящий анализ

Суть нисходящего анализа состоит в следующем. Предполагаем, что утверждение А, которое следует доказать истинно. Подбираем следствие В из него, следствие С из В и так до тех пор, пока не получим истинное утверждение. Проверяем обратимость наших утверждений. Делаем вывод.

Примеры.

№1. Доказать, что если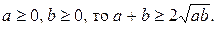

Начинаем с того, что следует доказать, предполагая, что неравенство верно.

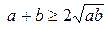Пусть истинно. Подбираем следствие.

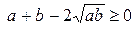истинно,

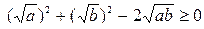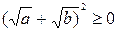истинно. Проверяем обратимость наших утверждений и делаем вывод, что неравенство доказано.

№2. Доказать, что в равнобедренной трапеции квадрат диагонали равен квадрату боковой стороны, сложенному с произведением оснований.

Дано: ABCD – трапеция,

АВ=CD.

Доказать: .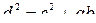

Нисходящий анализ.

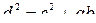Пусть 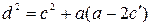истинно.

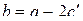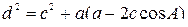истинно ( ).

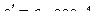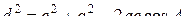истинно

(доказанная теорема косинусов).

Все рассуждения обратимы, следовательно, равенство доказано. Отметим, что запись доказательства следует начинать с последней строчки, и тогда придём к утверждению, которое следует доказать.

№3. Доказать, что если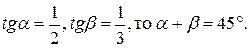

Нисходящий анализ.

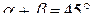Пусть 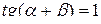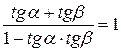истинно.

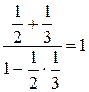истинно.

1=1 истинно.

Однако утверждение нельзя считать доказанным, так как если 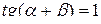истинно, то из него не следует, что 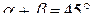истинно (необратимое рассуждение).

Восходящий анализ

Суть восходящего анализа состоит в следующем. Пусть следует доказать утверждение А. Подбираем утверждение В, из которого следует утверждение А, затем – утверждение С, из которого следует утверждение В и так далее, пока не получим истинное утверждение. Так как В Þ А, то В – достаточное условие А. Поэтому восходящий анализ сопровождается словами «для того, чтобы доказать А достаточно доказать В; для того, чтобы доказать В достаточно доказать С…» Заметим, что проверять обратимость утверждений восходящий анализ не требует.

Примеры.

№1.

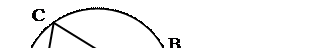Доказать, что если через точку, взятую внутри круга, проведены две произвольные хорды, то произведение длин отрезков каждой из хорд равны.

Дано:

круг,

АВ, CD – хорды,

О – точка пересечения хорд.

Рис. 36

Доказать: АО×ОВ=СО×ОD.

Восходящий анализ.

Для того, чтобы доказать равенство АО×ОВ=СО×ОD,

достаточно доказать ,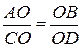

достаточно доказать DАОС~DDОВ,

достаточно доказать Ð1=Ð2, Ð3=Ð4 истинно, так как

вертикальные углы равны и

вписанные углы, опирающиеся

на одну и ту же дугу равны.

Запись доказательства следует выполнять с последней строчки.

Ценность анализа и синтеза состоит в том, что они являются средством поиска решения задачи, доказательство теоремы. Используя их, учащиеся могут самостоятельно доказать многие (конечно не все) теоремы самостоятельно. Например, свойства и признаки параллелограмма, прямоугольника, ромба, признак перпендикулярности прямой и плоскости и ряда других.

Индукция и дедукция

Индукцию рассматривают как один из видов умозаключения, как метод исследования, как форму изложения учебного материала. Смысл применения индукции в каждом из названных случаев заключается в словах «от частного к общему».

Примеры.

№1.

Рассмотрим частные суждения:

Окружность, эллипс, парабола, гипербола пересекаются с прямой не более, чем в двух точках.

Окружность, эллипс, парабола, гипербола – кривые второго порядка. Индуктивное умозаключение: все кривые второго порядка могут пересекаться с прямой не более, чем в двух точках. Это истинное утверждение.

№2.

Исследуем значения функции f(n)= n²-n+41 при nÎN.

Заполним таблицу

n	1	2	3	4	5	6	7	8	9	10
f(n)	41	43	47	53	61	71	83	107	113	131

На основании рассмотренных значений можно прийти к выводу, что при лбом натуральном значении п значение данной функции - простое число. Вывод оказывается неверным. Так, при п = 41 f(41)=41²-41+41, f(41)=41² – составное число.

В учебниках математики 5-6 классов материал изложен зачастую индуктивно: от частных примеров к общему выводу.

Виды индукции

Индукция бывает полная и неполная. Полная индукция предполагает рассмотрение всех частных случаев. Она является методом доказательства.

Например, теорема об угле, вписанном в в окружность доказывается методом полной индукции для трёх случаев: центр окружности принадлежит стороне угла, лежит между его сторонами, лежит вне угла.

Рис. 37

Методом полной индукции можно доказать, что всякое чётное число большее 2, но меньше 14 можно представить в виде суммы двух простых чисел. Составим их полный список: 4, 6, 8, 10,12. Тогда 4=2+2, 6=3+3, 8=3+5, 10=3+7=5+5, 12= 5+7. Все частные случаи рассмотрены. Утверждение доказано.

Неполная индукция заключается в том, что рассматриваются не все частные случаи. Неполная индукция не есть метод доказательства, однако она является мощным эвристическим средством, с помощью которого, рассматривая частные случаи, учащиеся самостоятельно приходят к общим выводам (верным или неверным). Известно, что индуктивный метод и в науке привёл к ряду гипотез (проблема Гольдбаха, Теорема Ферма).

Дедукция

Дедукция (от латинского deductio – выведение) есть форма умозаключения, при которой от общего суждения переходят к частному суждению. Дедукция представляет собой форму умозаключения, состоящую в том, что новое суждение выводится чисто логическим путём, то есть по определённым правилам логического вывода (следования) из некоторых известных суждений.

Впервые теория дедукции (логического вывода) была разработана Аристотелем. Особое развитие она получила в виде теории доказательств в математической логике.

Существенным различием между индукцией и дедукцией является характер заключения. Заключение по индукции лишь правдоподобно, заключение по дедукции достоверно, если истинны посылки и верно применено одно из правил логического вывода.

Приведём пример дедуктивного умозаключения.

Суждения: любой квадрат – ромб, любой ромб – параллелограмм. Дедуктивный вывод: любой квадрат – параллелограмм. Правило вывода – правило силлогизма. Суждение «любой квадрат – параллелограмм» истинно, так как истинны посылки и в основе его вывода использовано правило силлогизма. Широкое применение дедукции в математике обусловлено аксиоматическим методом построения математических теорий, основанном на некоторых предложениях, истинность которых признаётся без доказательств. Истинность же остальных предложений этой теории устанавливается с помощью дедуктивных доказательств, то есть все остальные предложения теории логически выводятся (дедуцируются) из предшествующих им предложений. Вот почему математику называют дедуктивной наукой.

Литература

2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев. - М.: Просвещение, 2002.

4. Груденов Я. И. Совершенствование методики работы учителя математики: кн.для учителя / Я.И. Груденов. – М. Просвещение, 1990.

Вопросы и задания к зачёту по общей методике обучения математике

I . Математические понятия

1. Что составляет объём понятия «четырёхугольник»?

2. Что составляет содержание понятия «четырёхугольник»?

3. Посредством чего раскрывается объём и содержание понятия?

4. Перечислите виды определений.

Назовите виды следующих определений.

1) Квадратным корнем из числа а называется число, квадрат которого равен а.

2) Трапецией называется четырёхугольник, у которого только две противоположные стороны параллельны.

3) Пусть О – фиксированная точка и Х – произвольная точка плоскости. Отложим на продолжении отрезка ОХ за точку О отрезок ОХ¢, равный ОХ. Точка Х¢ называется симметричной точке Х относительно точки О.

4)Функция называется чётной, если для любого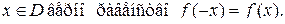

5. В чём состоит роль определений?

6. Как распознать трапецию?

7. Какие методы формирования понятий Вам известны?

8. Опишите любой метод формирования понятия.

II . Теоремы

1. Теорема – это …

2. Укажите вид формулировки теоремы.

1) В параллелограмме диагонали пересекаются и точкой пересечения делятся пополам.

2) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Следует ли учить школьников формулировать теорему в разных видах и почему?

3. Для теоремы «Сумма смежных углов равна 180°» сформулируйте обратное утверждение, противоположное и противоположное обратному. Как связана между собой истинность этих утверждений?

4. Представим теорему в виде «Если Р(х)ÞQ(х)».

Q(х) – это…

Р(х) – это …

Сформулируйте теорему из пункта (3) в терминах “необходимо” и ”достаточно”.

5. При каком условии необходимость является достаточностью?

6. Продолжите запись.

Для того чтобы четырехугольник был параллелограммом необходимо и достаточно, чтобы его противоположные стороны были равны.

Необходимость. Достаточность.

Дано: Дано:

Доказать: Доказать:

7. Охарактеризуйте этапы работы над теоремой до её доказательства.

III . Задачи

1. Какова роль задач в обучении?

2. Определите роль следующих задач.

№1. Два мальчика купили бананы. Один сказал другому: «Дай мне два твоих банана и у нас будет поровну». Другой ответил: «Дай мне два твоих банана и у меня будет в два раза больше, чем у тебя». Сколько бананов было у каждого?

№2. Мотоциклист ехал из одного города в другой 4 часа. На обратном пути первые 100 км он ехал с той же скоростью, а затем уменьшил её на 10 км/ч и поэтому на обратный путь затратил на 30 мин больше. Найти расстояние между городами.

№3. Желая доказать, что гипотенуза прямоугольного треугольника больше катета, ученик провел из вершины прямого угла А треугольника АВС такой луч АМ (М – на гипотенузе ВС), что ÐВАМ=0,5ÐС (рис 1). Как он собирался решать задачу?

3. Каковы функции задач в процессе обучения математике?

4. Приведите пример задачи и укажите её функцию.

5. Перечислите этапы решения задачи.

IV . Методы

1. Приведите классификацию методов обучения математике.

2. Перечислите научные методы. Почему они так называются?

3. Какой метод используется при введении распределительного закона умножения в 5 классе? В чём суть этого метода? Как он реализуется?

4. Какие виды анализа используются в обучении математике?

6. При исследовании функции и построении её графика какой вид анализа применяется?

7. В чём разница между нисходящим и восходящим анализом?

8. На примере задачи о произведении отрезков хорд проиллюстрируйте поиск решения методом восходящего анализа.

Лекции по методике обучения математике

Общая методика

Составитель: кандидат педагогических наук,

доцент кафедры информатики и

методики преподавания математики

Бондаренко Татьяна Евгеньевна

Воронеж

ВГПУ

2014

Содержание

1. Предмет методики обучения математике . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

2. Цели обучения математике в школе . . . . . . . . . . . . . . . . . . . . . . . . . . 3

3. Лекции по общей методике обучения математике . . . . . . . . . . . . . . . . . . . 5

3.1. Математические понятия и методика их формирования . . . . . . . . . . . . . . 5

3.2.Теоремы и методика их изучения в курсе геометрии средней школы. . . 17

3.3. Задачи в процессе обучения математике. . . . . . . . . . . . . . . . . . . . . . . . . . 29

3.4. Методы обучения математике . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

Дата: 2019-07-30, просмотров: 274.

12 3 4 5 6 7 Следующая ⇒