Проанализируем приведённое выше определение параллелограмма. В нём указано, из какого рода происходит параллелограмм (четырёхугольники), причём его ближайший род (не многоугольники), и видовое отличие (параллельность противоположных сторон). Аналогично составлено множество других определений: «линейной функцией называется функция, которая задаётся формулой вида 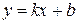, где k и b - числа, х – переменная»; «пирамида, называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника».

2. Конструктивные или генетические определения

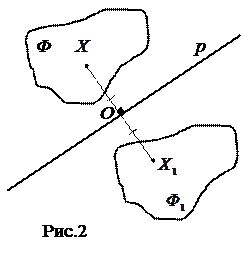 В конструктивных определениях содержание понятия раскрывается посредством описания происхождения объекта или способа его  образования. Например, «корнем п -ой степени из числа а называется такое число, п-ая степень которого равна а» или  «степенью числа а с натуральным показателем п (п≠1) называется произведение п множителей, каждый из которых равен а». В геометрии: «пусть F - данная фигура и р – фиксированная прямая. Возьмём произвольную точку Х фигуры и опустим перпендикуляр ХО на прямую р. На продолжении перпендикуляра за точку О отложим отрезок 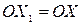. 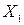Преобразование фигуры Ф в фигуру , при котором каждая точка Х переходит в точку , построенную указанным образом, называется симметрией

относительно прямой р».

 «Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым».

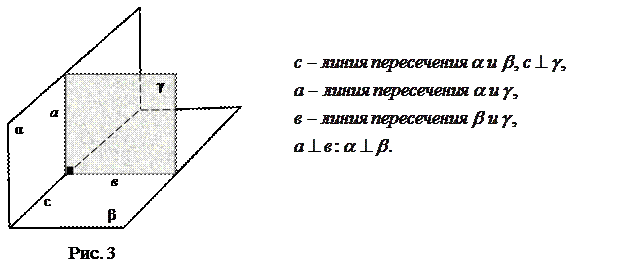
Иногда определение является классическим, но видовое отличие описывается конструктивно. Например, «пирамидой называется многогранник (род), который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания».

    Частным случаем генетических определений являются индуктивные определения, в которых указываются некоторые базисные элементы и правило, позволяющее получать новые элементы из уже имеющихся. Так, например, арифметическую прогрессию можно определить посредством двух чисел 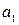, d и правила 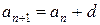(числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом).

    Перечисленные определения понятий относятся к так называемым явным. В них может быть выявлено определяемое и определяющее понятия. Однако определяющее понятие ранее также являлось определяемым. Например,  в  цепочке  понятий   «квадрат  →   ромб  →  параллелограмм →

четырёхугольник  →  многоугольник →  геометрическая фигура → множество точек» каждое предыдущее понятие определяется через следующее. Такую цепочку называют родословной понятия. Ясно, что она  не может быть бесконечной. Последние понятия в ней «множество», «точка» не определяются (так называемые основные понятия). Их свойства описываются в системе аксиом теории. Аксиомы рассматриваются как неявные определения основных понятий.

Структура определений

Наиболее часто встречаются определения конъюнктивной и дизъюнктивной структуры.

Если характеристические свойства  определяемого понятия соединены союзом «и», то структура определения – конъюнктивная, если союзом «или», то дизъюнктивная.

    Например, определение наибольшего общего делителя чисел а и в: «число с называется наибольшим общим делителем чисел а и в, если а делится на с и в делится на с и любой общий делитель чисел а и в делится на с» конъюнктивной структуры. Определение целых чисел: «числа натуральные, или им противоположные, или нуль называются целыми числами» - дизъюнктивной структуры.

    Существуют определения и других структур, иногда более сложных. Например, определение предела функции в точке. Некоторые определения имеют условную структуру: «если а≠0, то а⁰=1».Посредством определения раскрывается содержание понятия. Вместе с тем, определение служит средством распознавания объектов, принадлежащих объёму понятия.

Распознавание объекта (явления) по определению понятия – это умственное действие, состоящее в проверке у имеющегося объекта (явления)

наличия тех характеристических свойств, которые указаны в определении. Результатом распознавания является вывод о принадлежности объекта объёму понятия. Отметим, что педагогике вместо термина «распознавание» используется термин «подведение под понятие».

    Вывод о принадлежности или о непринадлежности объекта объёму понятия существенно зависит от структуры определения.

    Если структура конъюнктивная, то объект принадлежит объёму понятия, если ему присуще каждое характеристическое свойство, указанное в определении; если дизъюнктивная, – то хотя бы одно из этих свойств.

Например, распознать среди данных на рисунке  геометрических фигур четырёхугольники  – это значит проверить  наличие или отсутствие характеристических свойств, приведенных в определении четырёхугольника и сделать вывод, является ли данная фигура четырёхугольником.

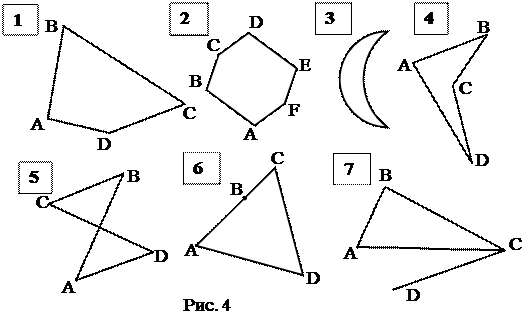
  Приведём определение из учебника геометрии А.В. Погорелова для  7-9 классов: «четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться». Так как структура определения конъюнктивная, то рассматриваемая фигура является четырёхугольником, если ей присуще каждое характеристическое свойство, указанное в определении.

Ответить на вопрос, какие из чисел -3,5; 101, 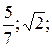 -18; 0 являются целыми – это значит проверить (распознать), какие из них – натуральные, им противоположные или 0. Причём число будет целым, если ему присуще хотя бы одно характеристическое свойство из определения, так как его структура дизъюнктивная.

Требования, предъявляемые к определениям

1.Отсутствие порочного круга. Порочный круг предполагает, что определяемое понятие явно или неявно содержится в определяющем.  

Контрпримеры.

1) Решение уравнения – это число, которое является его решением.

2) Угол называется прямым, если его стороны взаимно перпендикулярны. Две прямые называются взаимно перпендикулярными, если они образуют прямой угол.

2. Отсутствие омонимии: каждый термин должен встречаться не более одного раза в качестве определяемого, то есть один термин не должен обозначать разные понятия.

Контрпримеры.

1) Корень уравнения и корень из числа.

2) Квадрат – геометрическая фигура и произведение числа самого на себя.

3) Отношение двух чисел и бинарное отношение (параллельность, делимость).

Выбор ближайшего  рода.

Контрпример.

1) Параллелограммом называется многоугольник, у которого противолежащие стороны попарно параллельны.

4. Достаточность. Определение должно содержать все существенные свойства понятия.

Контрпримеры.

1) Прямые называются параллельными, если они не пересекаются.

2) Смежными называются углы, имеющие общую сторону.

3) Произведение чисел, переменных или их степеней называется одночленом.

Отсутствие избыточности.

Контрпример.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Следует отметить, что в школьном курсе математики такие определения приводятся, исходя из методических соображений.