Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

  Рассмотрим работу над теоремой в двух аспектах. Один из них связан с изучением теоремы начинающим учителем по учебнику, другой - с изучением этой же теоремы с учащимися в классе. Ниже приведена таблица, в которой представлены основные этапы такой работы.

 

 

№	Этапы работы над математическим содержанием теоремы	№	Этапы работы над методическим обеспечением доказательства теоремы на уроке
1.	Анализ формулировки теоремы: выделение условия и заключения. Выявление существенности основных элементов формулировки.	1.1. 1.2. 1.3.	Разработка средств, способствующих самостоятельному открытию учащимися математического факта, сформулированного в теореме. Иллюстрация существенности основных элементов формулировки, учёт возможных ошибок, подготовка соответствующих контрпримеров. Оформление чертежа, записи условия и заключения теоремы в форме «дано», «доказать».
2.	Выяснение проблемы, приводящей к необходимости доказательства теоремы, значения теоремы и её приложений в системе теорем раздела и всего курса.	2.	Обоснование (мотивировка) необходимости изучения теоремы. Характеристика роли теоремы.
3.	Выявление метода, идеи, приёма доказательства теоремы.	3.	Сообщение метода, идеи, приёма доказательства теоремы.
4.	Изучение доказательства. Составление плана (алгоритма доказательства).	4.1. 4.2. 4.3.	Разработка средств, способствующих самостоятельному отысканию доказательства учащимися. Составление алгоритма доказательства. Оформление записи доказательства.
5.	Выявление математического содержания (понятий, аксиом, теорем), на которых основано доказательство теоремы.	5.	Подготовка дидактических материалов, способствующих актуализации необходимых для усвоения теоремы знаний учащихся.
6.	Исследование математической ситуации, возникающей при доказательстве теоремы. Рассмотрение всех возможных случаев.	6.	Подготовка средств (вопросов, заданий, чертежей), способствующих исследованию математической ситуации.
7.	Рассмотрение других способов доказательства теоремы	7.	Обсуждение других способов доказательства теоремы.
8.	Составление комплекса учебных задач, способствующих усвоению теоремы.	8.	Решение комплекса учебных задач, способствующих усвоению теоремы.

  Рассмотрим методическое обеспечение на примере доказательства первого признака равенства треугольников по учебнику А.В. Погорелова.

1.1 Для самостоятельного открытия факта, сформулированного в теореме, учащимся предварительно может быть предложена практическая работа.

1 вариант.

Используя чертёжный треугольник с углом 60°, постройте треугольник АВС, такой что АВ=10 см, АС=12 см, ÐА=60°.

2 вариант.

Используя чертёжный треугольник с углом 60°, постройте треугольник А₁В₁С_1, такой что А₁В₁=10 см, А₁С₁=12 см, ÐА₁=60°.

  На уроке, измеряя стороны и углы, учащиеся придут к выводу о равенстве этих треугольников  по определению.

1.2. В формулировке теоремы существенно, что угол лежит между равными сторонами. Проиллюстрируем это на примере треугольников.

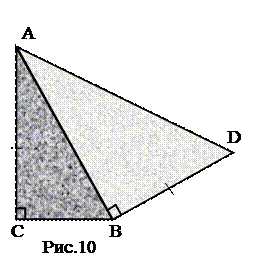Данные треугольники имеют общую сторону АВ, АС=BD и равные углы С и В. Не выполнено существенное условие теоремы: равные углы не лежат между равными сторонами. Очевидно, что треугольники не равны.

1.3.

В1

Дано: DАВС и DА₁В₁С₁.

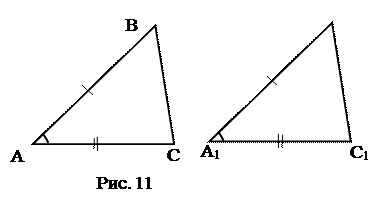
       АВ = А₁В₁, АС =А₁С₁,

       ÐА=ÐА₁.

Доказать: DАВС = DА₁В₁С₁.

 

2. По определению равенство треугольников предполагает наличие трёх пар равных элементов, признак сокращает их в 2 раза: до трёх пар равных элементов. Теорема играет важнейшую роль в курсе планиметрии, так как доказательство равенства треугольников станет основным методом доказательства.

3. Метод доказательства состоит в рассмотрении третьего треугольника

А₂В₂С₂, равного треугольнику АВС и совпадающего с треугольником А₁В₁С₁.

4.1. Самостоятельное доказательство теоремы учащимися в данном случае невозможно в связи с полным отсутствием опыта и сложностью метода доказательства.

4.2. Алгоритм доказательства:

1. Утверждаем существование треугольника А₂В₂С₂ равного треугольнику АВС и определённым образом расположенного относительно треугольника А₁В₁С₁.

2. Доказываем совпадение треугольников А₂В₂С₂ и А₁В₁С₁.

3. Делаем вывод о равенстве треугольников АВС и А₁В₁С₁

4.3.                                 Доказательство

1) По аксиоме VIII существует D А₂В₂С₂= D АВС:

вершина А₂ совпадает с вершиной А₁;

вершина С₂ принадлежит лучу А₁С₁;

вершина В₂ лежит в одной полуплоскости с вершиной В₁ относительно прямой А₁С₁.

	В1

 

 

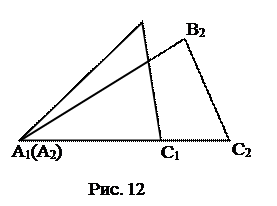
2) Докажем, что вершины С₁ и С₂ совпадают.

А₁С₁ = АС (по условию),

АС=А₂С₂  (так как DА₂В₂С₂=DАВС).

---------------------------------------------------

А₁С₁=А₂С₂.

Следовательно, по аксиоме откладывания отрезков точки С₁ и С₂ совпадают.

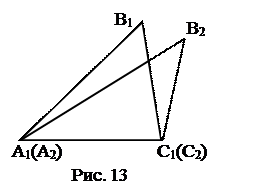Коррекция чертежа.

3) Докажем, что лучи А₁В₁ и А₂В₂ совпадают.

ÐА=ÐА₁ (по условию),

ÐА=ÐА₂ (так как DА₂В₂С₂=DАВС).

------------------------------------------------------

ÐА₁=ÐА₂.

Следовательно, по аксиоме откладывания углов лучи А₁В₁ и А₂В₂ совпадают.

Коррекция чертежа.

4) Докажем, что вершины В₁ и В₂ совпадают.

Доказательство аналогично пункту (1)

Коррекция чертежа.

5) Вывод. По аксиоме о о единственности прямой, проходящей через две точки, треугольники А₂В₂С₂ и А₁В₁С₁ совпали. По сути это два имени одного и того же треугольника. Так как DА₂В₂С₂=DАВС, то и А₁В₁С₁=DАВС. Что и требовалось доказать.

5. В доказательстве теоремы используется:

· аксиома откладывания отрезков (VI);

· аксиома откладывания углов (VII);

· определение равных треугольников.

· аксиома существования треугольника, равного данному (VIII);

· аксиома о единственности прямой, проходящей через две точки (I).

  В соответствии с приведённым списком учащимся могут быть предложены следующие задания на актуализацию знаний.

№1. На полупрямой а от её начальной точки B отложили два равных отрезка BM и BK. Что можно сказать о точках М и К? Обоснуйте ответ.

№2. От полупрямой а в одну и ту же полуплоскость отложены два равных угла (ав) и (ас). Что можно сказать о лучах а и с? Обоснуйте ответ.

№3. Сформулируйте аксиому существования треугольника, равного данному.

№4. Что означает выражение «Треугольник DAK равен треугольнику MNB»?

№5. Сколько равенств отрезков и углов определяют равенство треугольников?

6. В данном случае математическая ситуация исследована. Другие случаи не рассматриваются.

7. Иные способы доказательства не рассматриваем.

8. Приведём примеры задач по готовым чертежам, способствующих усвоению первого признака равенства треугольников.

Найти пары равных треугольников и доказать их равенство.

 

 

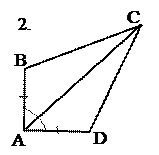
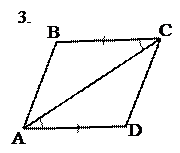
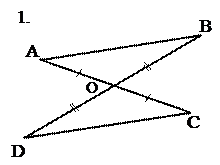
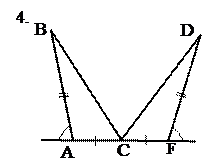
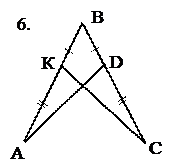
                                                  Рис. 16

 

Литература

1. Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н.Л. Стефановой. – М., Дрофа, 2005.

2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев, - М.: Просвещение, 2002.

3. Методика преподавания математики в средней школе: общая методика, Учеб. пособие для студентов пед. ин-тов / составители Р. С. Черкасов, А. А. Столяр. – М., Просвещение, 1985.

4. Погорелов А.В. Геометрия. 7- 9 классы: учебник для общеобразоват. учреждений / А.В. Погорелов. - 13-е изд. – М.: Просвещение, 2012 г.