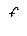Институт Металлургии, Машиностроения и Транспорта
Кафедра «Автоматы»
к.т.н., доц. Братчиков А.Я. ст. преподаватель Никитин А.В.
КУРСАВОЕ ПРОЕКТИРОВАНИЕ
Проектирование инструмента
С. Петербург 2016г.
ОГЛАВЛЕНИЕ
I. ФАСОННЫЕ РЕЗЦЫ... 5
1.ПРОЕКТИРОВАНИЕ ФАСОННОГО ДИСКОВОГО РЕЗЦА.. 19
1.1 МЕТОДИКА РАСЧЕТА ДИСКОВОГО ФАСОННОГО РЕЗЦА.. 19
1.1.1. Исходные данные: 19
1.1.2. Выбор базовой точки на профиле детали. 19
1.1.3. Выбор количества узловых точек N на профиле детали. 19
1.1.4. Выбор инструментального материала. 19
1.1.5. Выбор основных параметров дискового фасонного резца. 19
1.1.6. Выбор геометрических параметров режущей части резца. 21
1.1.7. Определение высоты установки резца относительно линии центров станка 22
1.1.8. Определение расстояния от оси резца до плоскости передней поверхности 22
1.1.9. Определение длины резца (см. рис.1.1.4) 22
1.1.10. Определение размеров стружечной канавки. 22
1.1.11. Коррекционный расчет профиля резца. 22
1.1.12. Назначение допусков и технические условия. 23
1.2. ЧИСЛОВОЙ ПРИМЕР РАСЧЕТА ДИСКОВОГО ФАСОННОГО РЕЗЦА 24
1.2.1. Исходные данные. 24
1.2.2. Выбор базовой точки на профиле детали. 24
1.2.3. Выбор количества узловых точек N на профиле детали. 24
1.2.4. Выбор инструментального материала. 24
1.2.5. Выбор основных конструктивных параметров дискового фасонного резца 25
1.2.6. Выбор геометрических параметров режущей части резца. 25
1.2.7. Высота установки резца относительно линии центров. 25
1.2.8. Расстояние от оси резца до плоскости передней поверхности. 25
1.2.9. Определение длины резца. 25
1.2.10. Выбор глубины заточки. 25
1.2.11. Коррекционный расчет профиля резца. 26
II. ПРОТЯЖКИ.. 27
ПРОЧНОСТЬ ПРОТЯЖЕК.. 45
2. МЕТОДИКА РАСЧЕТА КРУГЛОЙ ПРОТЯЖКИ.. 47
2.1. Исходные данные. 47
2.3. Определение подачи на зуб у режущих зубьев протяжки. 48
2.4. Суммарный подъем на зачищающие (чистовые) зубья. 49
2.5. Расчетная глубина впадины зубьев протяжки. 49
2.6. Расчетный шаг режущих зубьев. 50
2.7. Форма и размеры стружечной канавки в осевом сечении. 50
2.8.Определение геометрических параметров зубьев протяжки. 54
2.9. Максимальное число одновременно работающих зубьев протяжки 55
2.10. Наибольшее усилие протягивания. 55
2.11.Определение размеров хвостовика. 57
2.12. Диаметр передней направляющей части протяжки. 57
2.13. Проверка протяжки на прочность. 58
2.14.Определение размеров калибрующих зубьев протяжки. 61
2.15. Профиль и число калибрующих зубьев. 63
2.16. Число режущих зубьев. 64
2.17. Число и размеры стружкоразделительных канавок для режущих зубьев. 64
2.18. Определение общей длины протяжки (см.рис.2.1.4) 65
2.19. Определение допустимого радиального биения на режущих зубьях протяжки. 67
2.2. Числовой пример расчета круглой протяжки. 67
2.2.1. Исходные данные. 67
2.2.2. Определение припуска под протягивание. 67
2.2.3. Диаметр сверла D св для отверстий. 68
2.2.4. Определение подачи Sz на зуб у режущих зубьев протяжки. 68
2.2.5. Назначение суммарного подъема 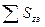 на зачищающие (чистовые) зубья протяжки. 68
на зачищающие (чистовые) зубья протяжки. 68
2.2.6. Расчетная глубина hp впадины зуба протяжки. 68
2.2.7. Расчетный шаг Pp режущих зубьев. 68
2.2.9. Определение геометрических параметров зубьев протяжки. 68
2.2.10. Максимальное число одновременно работающих зубьев протяжки 69
2.2.11. Наибольшее усилие протягивания составит (см. табл.2.1.7...2.1.9) 69
2.2.12. Размеры хвостовика назначаем по табл. 2.1.10. 69
2.2.13. Диаметр передней направляющей равен. 69
2.2.14. Проверка протяжки на прочность. 69
2.2.15. Определение размеров калибрующих зубьев потяжки. 70
2.2.16. Профиль и число калибрующих зубьев. 70
2.2.17. Число режущих зубьев. 71
2.2.18. Число и размеры стружкоразделительных канавок. 71
2.2.19. Общая длина протяжки L П (рис.2.1.4) 71
2.2.20. Допустимое радиальной биение на режущих зубьях протяжки. 72
III. ЧЕРВЯЧНЫЕ ФРЕЗЫ... 73
3. Зуборезные червячные фрезы... 75
3.1. МЕТОДИКА РАСЧЕТА ЧЕРВЯЧНОЙ ФРЕЗЫ... 84
3.1.1. Исходные данные. 84
3.1.2. Определение параметров исходной инструментальной рейки показано на рис.3.1.1 (см.табл.3.1.1). 84
3.1.3. Расчетный профильный угол 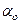 , инструментальной рейки в нормальном сечении (профильный угол фрезы) 84
, инструментальной рейки в нормальном сечении (профильный угол фрезы) 84
3.1.4. При нарезании прямозубого колеса (β=0) нормальный модуль mn . фрезы принимается равным модулю m 0 колеса. 85
3.1.5. Шаг по нормали Р no, между соседними профилями фрезы (рис.1) 85
3.1.6. Расчетная толщина зуба Sno фрезы по нормали к делительной окружности 85
3.1.7. Высота головки и ножки фрезы определяется по формуле. 85
3.1.8. Определение высоты hu . зуба фрезы. 85
1.9. Выбор типа и основных размеров фрезы (ГОСТ 9324-80). 85
3.1.10. Определение угла Ψ контакта фрезы.. 87
3.1.11. Число зубьев фрезы определяется по формуле: 87
3.1.12. Выбор геометрических параметров зуба фрезы. 87
3.1.14. Диаметр начальной окружности (табл.4) 90
3.1.15. Угол подъема витков фрезы на начальной окружности. 90
3.1.16. Осевой шаг фрезы.. 90
3.1.17. Определение угла установки фрезы на станке. 90
3.1.19. Наименьшая длина нарезанной части фрезы определяется по формуле 90
3.1.20. Расчетные размеры зубьев фрезы в нормальном сечении. 91
3.2. Числовой пример расчета червячной фрезы.. 91
3.2.1. Исходные данные. 91
3.2.2. Параметры зубьев колеса (зубчатой рейки) 91
3.2.3. Расчетный профильный угол  инструментальной рейки в нормальном сечении (профильный угол фрезы) для эвольвентного зацепления
инструментальной рейки в нормальном сечении (профильный угол фрезы) для эвольвентного зацепления  .................. 91
.................. 91
3.2.4. Нормальный модуль фрезы принимаем равным модулю колеса (прямозубое колесо) 91
3.2.5. Шаг по нормали Pno между соседними профилями фрезы (см. рис.3.1.1) 91
3.2.6. Расчетная толщина зуба Sno по нормами к делительной окружности 91
3.2.7. Высота головки и ножки зуба. 91
3.2.8. Высота зуба фрезы.. 91
3.2.9. Выбор типа фрезы.. 92
3.2.10.Угол контакта фрезы.. 92
3.2.11. Число зубьев фрезы.. 92
3.2.12. Геометрические параметры зубьев фрезы принимаем  ........ 92
........ 92
3.2.13. Падение затылка. 92
3.2.14.Диаметр начальной окружности фрезы.. 92
3.2.15 Угол подъема витков фрезы на начальной окружности. 92
3.2.16. Осевой шаг фрезы.. 93
3.2.17. Угол остановки фрезы на станке. 93
3.2.18.Глубина стружечной канавки (для нешлифованного зуба) 93
3.2.19 Наименьшая длина на нарезанной части фрезы.. 93
3.2.20. Уточнение размеров зубьев фрезы в нормальном сечении. 93
ПРИЛОЖЕНИЯ.. 94
Приложение 3.1
Параметры шероховатости и точности обработки поверхностей червячных зуборезных фрез. 94
Приложение 3.2
Контроль точности изготовления фрез. 95
Приложение 3.3
Размеры профиля зубьев фрез в осевом сечении. 97
Приложение 3.4
Размер шпоночных пазов в инструменте, мм.. 98
ЛИТЕРАТУРА.. 99
I. ФАСОННЫЕ РЕЗЦЫ
Фасонные резцы широко применяют в массовом и крупносерий-
ном производстве для обработки сложного профиля деталей тел
вращения или призматических деталей. На деталях тел вращения
обрабатывают как наружные, так и внутренние поверхности на
токарных, револьверных станках, полуавтоматах и автоматах. Фа-
сонные поверхности на призматических деталях изготовляют фасон-
ными резцами на фрезерных и строгальных станках.
Фасонные резцы имеют ряд преимуществ по сравнению с обыч-
ными токарными резцами. Они обеспечивают:
1)высокую производительность вследствие значительного умень-
шения машинного и вспомогательного времени за счет сокращения
пути резания при радиальной подаче и времени на установку и
наладку резца;
2) высокую точность формы и размеров обрабатываемых деталей,
а также их идентичность и взаимозаменяемость;
3) простоту эксплуатации, так как их перетачивают только
по передней поверхности.
Однако стоимость фасонных резцов выше, чем простых токарных
резцов. Несмотря на это, в массовом и крупносерийном производстве
они вполне рентабельны. Фасонные резцы подразделяют по форме
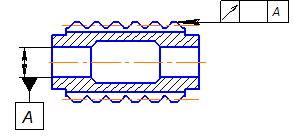
на круглые и призматические (рис, 1.1.а, б); по виду обрабатывае-
мой поверхности – на наружные и внутренние (рис. 1.1.а, г); по
установке и направлению подачи относительно обрабатываемой
детали – на радиальные и тангенциальные (рис. 1.1.б, в); по форме
образующих фасонных поверхностей — на кольцевые и винтовые
(рис. 2.1.е, ж, и); по расположению резца относительно детали – с параллельным расположением осей или баз или с повернутым
(рис. 2.1.е, ж) и по расположению передней поверхности – без
наклона и с наклоном под углом л (рис. 1.1.а, д). Призматические
резцы изготовляют только для обработки наружных поверхностей.
Круглые резцы, как правило, работают с радиальной подачей и их применяют для обработки как наружных, так н внутренних поверх-
ностей. При этом для последних применяют кольцевые и винтовые
резцы.
Рис. 1.1. Типы фасонных резцов
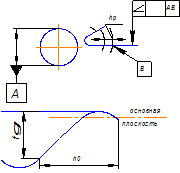
Причины искажения профиля фасонного резца. Профиль фасонного резца определяется в сечении, нормальном к его задней поверхности. В этом сечении рассчитывают и задают размеры профиля и
осуществляют его контроль. Однако формообразующей поверхностью детали является режущая кромка. Профиль резца в нормальном сечении не совпадает с линией режущей кромки. В свою очередь, линия режущей кромки резца может отличаться от профиля обработанной детали в ее осевом сечении. Следовательно, профиль фасонного резца отличается от профиля обработанной детали. Причиной этого несоответствия является наличие у резца переднего и заднего углов. Для уяснения этого вопроса рассмотрим рис. 1.2.
Возьмем один участок детали в виде усеченного конуса. В первом случае (рис.1.2, а), когда передний н задний углы резца равны
нулю, высота профиля резца B1 равна разности радиусов обработанной детали, т. е. В1 = r2 - r1. Профиль резца соответствует режущей кромке и профилю детали. Но это нереальный случаи, т.е. резец не может иметь нулевой задний угол. Заметим, что для неповернутых резцов их размеры в осевом направлении детали не изменяются.
Во втором случае (рис. 1.2, б) у резца передний угол γ1>О,
а задний угол α1 = 0. При этом высота профиля резца В2<( r2 - r1),
т. е. меньше В1. Отсюда следует, что если угол γ≠0, то профиль
резца будет отличаться от профиля режущей кромки, а значит и от профиля обрабатываемой детали.
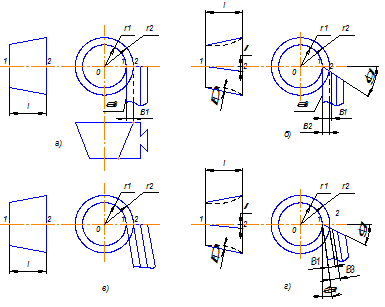
Рис. 1.2. Влияние γ и α на высоту профиля резания
В третьем случае (рис. 1.2, в) угол γ = 0, а угол α > 0. Здесь также высота профиля резца меньше высоты профиля детали, т. е. В3<( r3 — r1); В= B1· cosα1.Следовательно, задний угол также создает отклонение профиля резца от профиля детали. Наконец, последний случай (рис. 1.2, г) соответствует реальным условиям, когда у резца α>0 и γ>0. В этом
случае B4<В3 и В4<В2. Таким образом, совместное влияние перед-
него у и заднего а углов увеличивает отклонение профиля резца
от режущей кромки и от профиля детали.
Будем считать передние и задние углы основными причинами,
которые вызывают указанное отклонение. Это отклонение не создаст
погрешность, оно является необходимым, преднамеренным. Вследствие этого профиль фасонного резца должен быть определен расчетным путем. Только при таком определенном отличии профиля резца
от профиля детали, которое устанавливается расчетным путем, за-
данная деталь будет обработана точно.
Профилирование фасонных резцов. Существуют графический
и аналитический методы определения профиля фасонных резцов.
Графический метод наглядный, но неточный, поэтому в инженерной
практике не применяется. Аналитический метод лишен этого не-
достатка, но более сложный. Несмотря на это, высокие требования
к точности проектирования фасонных резцов обусловили применение на практике аналитического метода. Существует несколько способов расчета профиля фасонных резцов. Рассмотрим общий способ точного аналитического решения задачи профилирования резцов, а также один из способов, основанный на решении трехчленных уравнений, который является также точным, но простым и наглядным.
Таблица 1.1.
Значения переднего угла для фасонных резцов
Обрабатываемый
Материал
Сталь σв, МПа
Чугун, НВ
Латунь
Бронза
Свинцови-
Стая
Красная
Медь, алюминий
Решение задачи сводится к тому, чтобы определить необходимый
профиль резца в нормальном сечении к его задней поверхности,
при котором режущие кромки резца могли бы правильно обработать
заданную деталь. Исходными параметрами для расчета являются
размеры обрабатываемой детали, заданные чертежом, и свойства
обрабатываемого материала. Вначале задаются значением переднего
и заднего углов резцов. Для фасонных резцов из быстрорежущей
стали, работающих с радиальной подачей, оптимальный задний
угол α = 10...150. Для резцов из твердого сплава α = 8...120. Передний угол у в зависимости от свойств обрабатываемого материала для
резцов из быстрорежущей стали рекомендуется принимать по
табл. 1.1. Для резцов из твердого сплава передний угол принимают
на 5...100 меньше.
Фасонные резцы можно устанавливать по высоте центров обрабатываемой детали (по центру) одной вершинной точкой или же
линией – режущей кромкой. В последнем случае это может быть
только для цилиндрического или конического участка детали. Для
поверхностей криволинейного профиля или торцовых этого достигнуть невозможно. На практике чаще применяются резцы первого
вида, устанавливаемые по центровой линии детали одной точкой,
расположенной в вершине режущей кромки. Для обработки наружных поверхностей тел вращения эта точка контакта находится
на наименьшем диаметре обрабатываемой детали; для обработки
внутренних поверхностей – на наибольшем диаметре отверстия.
Общий аналитический способ профилирования резцов. Для определения профиля фасонного резца общим аналитическим способом
необходимо найти режущую кромку как линию пересечения поверх-
ности детали с плоскостью передней грани резца, принять ее за об-
разующую поверхности резца и определить линию сечения резца
плоскостью, нормальной к задней поверхности инструмента. Для
этого необходимо решить следующие задачи.
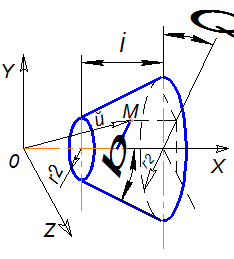
Рис. 1.3. К определению уравнения конической поверхности детали
1.Записать уравнение поверхности заданной детали в системе XYZ (рис.1.3). Для участка детали в виде усеченного конуса параметрическое уравнение такой поверхности имеет вид:
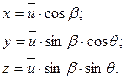 1.1
1.1
Здесь параметры ū и θ изменяются в диапазонах 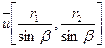 ;
; 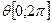 , где r1 и r2 – наименьший и наибольший радиусы детали; β – угол наклона образующей конуса.
, где r1 и r2 – наименьший и наибольший радиусы детали; β – угол наклона образующей конуса.
Если учесть, что из первого уравнения системы (1.1) 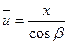 ,
,
то эту систему уравнения можно записать
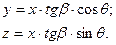 1.2
1.2
В уравнениях (1.2) абсциссой х задаются.
2. Уравнение плоскости 1 – 2 передней поверхности резца в си-
стеме координат XYZ имеет вид (рис. 1.4)
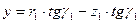 1.3
1.3
где γ1 – передний угол резца в расчетной точке 1.
3. Решив совместно уравнения (1.2) и (1.3), получим уравнения
линии режущей кромки резца в системе координат детали XYZ
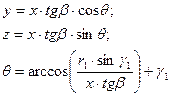 1.4
1.4
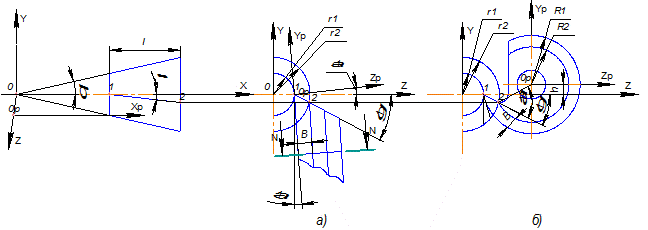
Рис. 1.4. Схема для аналитического профилирования фасонного резца: а – призматического; б – круглого
4. Преобразуем систему координат XYZ в систему Xр Yр Zр,
связанную с резцом. Для призматического резца (рис. 1.4, а) эта связь координат точек режущей кромки определяется матричным;
равенством
 1.5
1.5
где М – матрица перехода из системы XYZ в систему XPYPZр.
В соответствии с рис. 1.4, а матрица
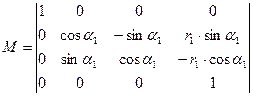 1.6
1.6
Тогда формулы перехода из системы XYZ в систему XPYPZр.
примут вид
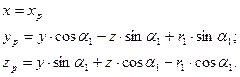 1.7
1.7
где α1 – задний угол резца в точке 1.
5. Подставив в уравнения (1.7) формулы для координат y, z
из уравнений (1.4), получим координаты точек, т. е. уравнения ре-
жущей кромки призматического резца в системе ХРУ p Zp
 1.8
1.8
Введем неподвижную систему координат X' P Y' P Z' P, совпадающую
вначале с системой XPYр Zр, которую принимаем за подвижную.
Для образования задней поверхности резца сообщим подвижной системе координат, а вместе с ней и режущей кромке движение вдоль
оси Y' P. Тогда уравнение этой поверхности запишется
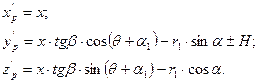 1.9
1.9
где Н – текущее значение параметра, формообразующего заднюю
поверхность.
Плоскость, нормальная к задней поверхности резца, есть координатная плоскость X' P Y' P или любая другая, параллельная ей, уравнение которой y' P = 0 или y' P = ± Н.
6. Если принять y' P = 0, то искомый профиль призматического фасонного резца в сечении нормальной плоскостью запишется
уравнением
 1.10
1.10
Анализ уравнения (1.10) показывает, что профиль резца получается криволинейным (вогнутым). Если режущую кромку совместить с образующей конуса так, чтобы λ = 0, то она будет прямолинейной. В этом случае профиль призматического резца будет тоже
прямолинейным. Для образования круглого резца найденной режущей кромке необходимо сообщить круговое движение относительно
оси резца Хр. Задача по отысканию профиля круглого фасонного
резца в нормальном (осевом или радиальном) сечении сводится
к определению расстояний точек режущей кромки, описываемой
уравнением (1.4), до оси круглого резца.
Положение оси резца задается координатами ур и rр (рис. 1.4, б),
которые определяются через исходные постоянные величины r1,
R1 и α1,:
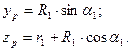 1.11
1.11
Ось круглого резца в системе XyYpZp проще задать единичным
вектором ī с направляющими коэффициентами
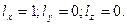 1.12
1.12
который проходит через точку центра резца с координатами хр, yр, zР.
Расстояние R от точки режущей кромки с координатами х, у, z
до прямой ī (lx, ly, lz), заданной единичным вектором (1.12) и про-
ходящей через ось Хр резца, определяется по формуле
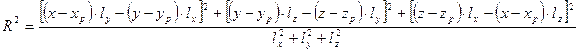 1.13
1.13
Подставив в формулу (1.13) значения x, y и z из уравнения (1.4)
и учитывая коэффициенты lx, ly, lz и координаты точки Ор (О, ур, zp),
получим уравнение для определения искомого радиуса резца
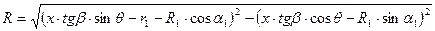 1.14
1.14
где угол θ находится из совместного решения уравнении (1.2) и (1.3):
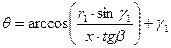 1.15
1.15
Зная разность радиусов R1– R резца и его осевые размеры,
находим профиль инструмента. Высота профиля В= R1– R. Для
точного определения профиля резца в уравнении (1.14) необходимо задаться рядом значений текущих осевых размеров х детали и для
каждого из них найти радиус R. Обычные вычисления окажутся
слишком трудоемкими, поэтому данную задачу целесообразно решать на ЭВМ, используя формальные языки программирования.
Преобразуем третье уравнение системы (1.10) к виду, позволяющему находить угол θ как функцию его тангенса:
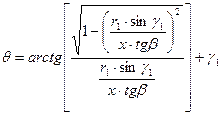 1.16
1.16
Введем в формулу (1.16) обозначения: S1 = r1 · sinγ, S2 = x· tg β; S3 = S1/ S2, после чего выражения (1.14) и (1.16) примут
вид
 1.17
1.17
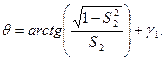 1.18
1.18
При заданном числе точек n на оси X от xmin до х max определим
шаг Δ x изменения координаты х:
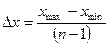 1.19
1.19
Определение профиля фасонных резцов геометрическим способом.
Как уже отмечалось, этот способ основан на решении простых трех-
членных уравнений, широко используемых на практике. Пусть
размеры обрабатываемой детали заданы в соответствии с рис. 1.5.
С учетом качества обрабатываемого материала по табл. 1.1 выбираем
передний угол γ1. Задний угол α1 принимаем равным 10...120. Для
примера рассмотрим методику профилирования круглого фасонного
резца. Расчет профиля резца для обработки различных участков
детали ведут последовательно от одной базовой точки 1 или ли-
пни 1—1, в которой для неповернутых резцов его вершину устанавливают по высоте центров детали. Расчетная схема строится без
масштаба. Для конического участка детали 1—2 она показана на
рис. 1.6. Прежде всего определим исходный наружный диаметр Dl
резца или радиус R1. Для этого рассчитаем диаметр оправки d
из условия ее работы на сложное сопротивление. Исходный наружный диаметр резца D1≈(2,5...3)· d. Диаметр оправки принимают
из соотношения d≈0,4· l, где l – длина обрабатываемой детали.
Расчетные диаметры резца и оправки принимаются по приведенному
ниже нормальному ряду.
| d, мм | 12 | 16 | 20 | 22 | 24 | 28...30 | 32...36 |
| D, мм | 30...40 | 40...50 | 50...60 | 60...70 | 70...80 | 80...90 | 90...100 |
Центр круглого резца выше центра обрабатываемой детали на
величину h. Это необходимо, чтобы образовать задний угол α резца:
h = R1· sinα1, где α1 – задний угол резца в точке 1.
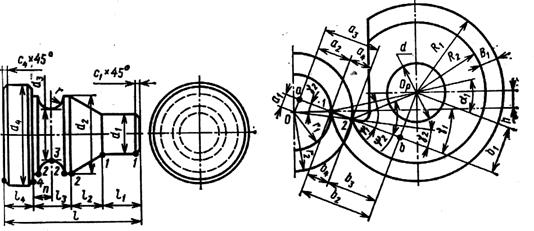
|
|
Методика определения профиля резца следующая. Сначала решают систему прямоугольных треугольников, связанных с обрабатываемой деталью, из которых находят
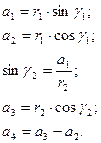
где γ2 – передний угол резца в точке 2 его контакта с деталью.
Затем решают систему двух прямоугольных треугольников, связанных с резцом, из которых
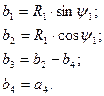
где ψ1 – уол искажения в точке 1, ψ1 = γ1 + α1, ψ2 – угол искажения в точке 2, ψ2= γ2+α2; tgψ2= 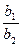 ; α2 – задний угол резца в точке 2. Тогда искомый радиус резца
; α2 – задний угол резца в точке 2. Тогда искомый радиус резца
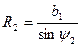 1.20
1.20
а высота профиля резца В1 = R1 – R2
Для условных (нереальных) участков 1–3 и 1–4 детали (см.
рис. 1.5) профиль резца рассчитывают таким же способом.
Определение профиля фасонного резца от одной
базовой точки 1 имеет то преимущество, что при построении расчетных схем для условных участков детали 1–3 1–4 и т.д. малый
треугольник Oa1, связанный с деталью, и большой прямоугольный
треугольник ОРВ1, связанный с резцом, остаются неизменными
(см. рис. 1.6). Поэтому их размеры определяются только один раз
по первой расчетной схеме. Вследствие этого сокращаются вычисления. Кроме того, найденные размеры профиля резца определяются
от этой базовой точки 1 или линии 1–1. Во всех случаях высота
профиля резца получается меньше высоты профиля обрабатываемой
детали. Анализ приведенных уравнений показывает, что профиль
фасонных резцов зависит от параметров обрабатываемой детали и
инструмента. Наибольшее влияние на профиль резца оказывает
угол конуса детали β, затем передний и задний углы и в меньшей
мере размеры резца.
Профиль резца по крайним точкам можно рассчитать только для
участков детали, имеющих торцовые уступы. Резцы, рассчитанные
таким способом для конических поверхностей, имеют погрешности
при обработке. Если передний угол положительный и режущая
кромка принимается прямолинейной, то она не будет совпадать с образующей конуса (рис. 1.7), а является наклонной к ней под углом λ.
Так как режущая кромка является формообразующей, то обработанная поверхность детали будет не конической, а вогнутой в виде
гиперболоида вращения. В результате возникнет погрешность Δ1
которую можно устранить, совместив режущую кромку с образующей конуса путем поворота резца на угол К или заточкой его перед-
ней поверхности под этим углом. Но так можно делать только для
деталей, состоящих из одного конического участка. Для сложного контура деталей, имеющих несколько участков, этого сделать нельзя. В более общем случае такая погрешность будет устранена, если для расчета профиля резца взять несколько точек (сечений) на конической поверхности детали. Тогда режущая кромка и профиль резца будут криволинейными – вогнутыми.

Рис. 1.7. Образование погрешностей детали круглым фасонным резцом.
Однако резцы с криволинейным профилем нетехнологичны. В ряде случаев сложная поверхность круглого резца заменяется более простой – конической. В этом случае режущая кромка резца будет выпуклой, так как она лежит в передней плоскости, которая не проходит через ось резца,
а отстоит от нее на расстоянии Н. В результате возникнет погрешность обработки детали, равная Δ2 (рис. 1.7). Суммарная погрешность обработки резцом конической формы Δ = Δ1 + Δ2. Выпуклость режущей кромки аналитически определена в работе [4].
На рис. 1.8 показана схема для решения этой задачи. Находим
наибольшее отклонение Δ y. Режущая кромка с наибольшей выпуклостью лежит в плоскости передней поверхности резца. Отклонение
Δ y есть проекция Δ2 на осевую плоскость резца, определяемое
в направлении, перпендикулярном его оси. Запишем уравнение
конической поверхности резца
 1.21
1.21
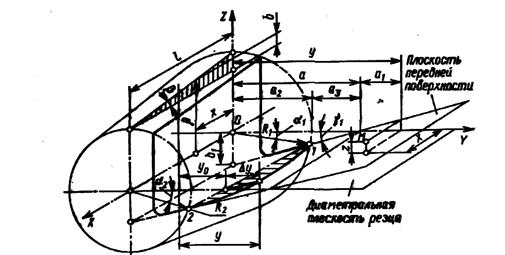
Рис. 1.8. Определение выпуклости режущей кромки резца
где b = х· tgβ; ρ – текущий радиус-вектор на конической поверхности резца; R1 — радиус резца в точке 1; β – угол наклона образующей конической поверхности резца.
Уравнение передней плоскости у=а+а1 где а=а2+а3;
а2 = R1· cos α1; a3 = R1· sin α1/ tg γ; а1 = z· ctgγ1
Таким образом, у = a – z· ctg γ1 или
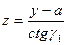 1.22
1.22
Решив совместно уравнения (1.21) и (1.22), получим квадратное
уравнение, которое описывает гиперболическую режущую кромку
резца 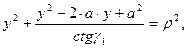 откуда
откуда
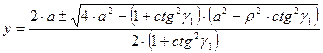 1.23
1.23
Из рис. 2.8 видно, что
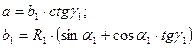 1.24
1.24
Подставим значение а в уравнение (1.23) и после некоторого преобразования получим окончательное уравнение режущей кромки I
резца
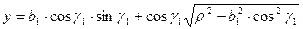 1.25
1.25
где γ1 – передний угол резца в точке 1.
Уравнение прямой линии, проходящей через крайние точки 1–2
(см. рис. 1.8) режущей кромки,
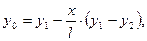 1.26
1.26
где y1 и y2 – ординаты точек 1 и 2. Из уравнения (2.21) имеем
 1.27
1.27
Подставив уравнение (1.27) в уравнение (1.26), получим
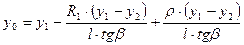 1.28
1.28
Величина стрелы выпуклости режущей кромки Δ y = у – у0 т. е.
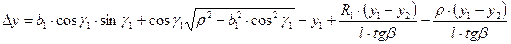 1.29
1.29
Максимальная выпуклость получится при значении ρ, для которого первая производная  .
.
Дифференцируя уравнение (1.29) и подставив значение b1, из (1.24) получим
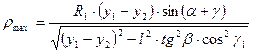 1.30
1.30
+
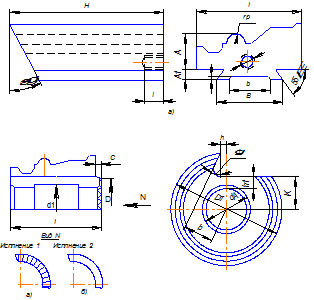
Рис. 1.9. Призматический (а) и круглый (б) фасонные резцы
Подсчитав по уравнению (1.30) ρmax и подставив его в уравнение (1.29), получим максимальную выпуклость режущей кромки
круглого конического резца, который установлен только одной
вершинной точкой на высоте центра изделия. Подставив значение ρmax в уравнение (1.27), получим значение абсциссы х, определяющей точку режущей кромки, к которой относится максимальная выпуклость. Исследования, приведенные в работе[1], показали, что наиболее точными являются призматические резцы, у которых прямолинейная режущая кромка совпадает с образующей конуса обрабатываемой детали. В этом случае не возникает погрешность обработки. Это справедливо и для призматических тангенциальных резцов.
Призматические резцы, устанавливаемые только одной точкой
режущей кромки по центру обрабатываемой детали, создают незначительную погрешность. Наибольшая погрешность возникает при
работе круглыми коническими резцами. Для конических резцов
95 % общей погрешности составляет выпуклость режущей кромки.
Детали, обработанные такими резцами, могут иметь вогнутость
0,5...1,5 мм. Задача по определению профиля призматических резцов решается более просто, чем для круглых. Для участка 1–2
высота профиля призматического резца В1= a4· cosψ1 (см. рис. 1.6).
Для радиусных участков деталей фасонные резцы профилируют по
приведенной выше методике. Задаются несколькими точками на
радиусном участке детали и находятся также координаты соответствующих точек профиля резца. Расчетный профиль резца получается криволинейным. Для несопряженных радиусных участков с невысокой точностью криволинейный профиль резца заменяют соответствующим радиусом.
Определение расстояния
ЧИСЛОВОЙ ПРИМЕР РАСЧЕТА
ДИСКОВОГО ФАСОННОГО РЕЗЦА
Исходные данные
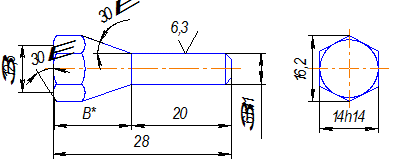
Рис. 1.1.2
Деталь – штуцер; заготовка – шестигранный пруток В = 14 мм; марка материала - сталь 45; твердость – I80 HB; предел прочности – σв = 650 МПа; размеры, точность и шероховатость обработанных поверхностей – рис.2.
Дискового фасонного резца
В зависимости от максимальной глубины профиля обрабатываемой детали по табл.1 определяем основные конструктивные параметры резца
D = 40h13; d = I3H8; d2 = 20 мм; l2 = 3 мм,
Рис. 1.1.3.
В зависимости от марки и физико-механических свойств обрабатываемого материала и марки (рис.1.1.3) инструментального материала по табл.1.1.2 для периферийной точки 6 профиля резца выбираем γ6 = 200; α6 = 120.
Определение длины резца
Расчет производим по схеме, изображенной на рис. 1.1.4, где указанные в скобках размеры относятся к числовому примеру.
Выбор глубины заточки
По максимальной глубине профиля детали tmax по табл.1.1.2 выбираем глубину выточки по передней поверхности резца К = 3 мм.
II. ПРОТЯЖКИ
Протягивание является одним из наиболее высокопроизводительных процессов обработки деталей резанием. Высокая производительность процесса протягивания объясняется тем, что одновременно находится в работе несколько зубьев инструмента с большой суммарной длиной режущих кромок. Исключение составляет протягивание деталей тел вращения, где это условие в большинстве случаев не соблюдается.
Протяжки позволяют получать поверхности высокой точности
(7...8-й квалитет) и низкой шероховатости (Ra 0,63...25 мкм). При
обработке отверстий протягивание с успехом заменяет зенкерование
и развертывание, а также чистовое растачивание.
При обработке наружных поверхностей по производительности;
точности и качеству обработанной поверхности протягивание во
многих случаях значительно эффективнее строгания, фрезерования,
а иногда и шлифования.
При правильной эксплуатации протяжки имеют высокую стойкость и долговечность. Однако протяжки – это сложный и дорогостоящий многолезвийный инструмент. Он узко специализирован для обработки одной или группы деталей с определенным контуром обрабатываемой поверхности, поэтому его применяют главным образом в массовом и крупносерийном производстве. В мелкосерийном производстве протяжки используют лишь тогда, когда другим способом нельзя получить необходимую точность поверхности детали, например, многошпоночных и многошлицевых отверстий. Другой случай рентабельного применения протяжек в мелкосерийном производстве, когда формы обрабатываемых поверхностей и их размеры нормализованы.
Для некоторых видов поверхностей, таких как эвольвентные,
шлицевые, винтовые отверстия, протягивание является единственным методом их формообразования. Протягивание инструментами из быстрорежущей стали производится при сравнительно низких скоростях резания 3...8 м/мин, получаемых в результате поступательного или вращательного движения протяжки. Исключением является обработка деталей тел вращения, когда окружная скорость вращения деталей 25..35 м/мин.
При протягивании движения подачи, как такового нет, так как
у протяжки каждый последующий зуб имеет превышение по высоте
и ширине относительно предыдущего. Это превышение называется
подъемом зуба протяжки, которое определяет толщину срезаемого
слоя. Ширина срезаемого слоя будет равна длине режущей кромки.
Протяжки подразделяются на внутренние и наружные. Внутренние протяжки служат для обработки отверстий как простых цилиндрических, так и сложного профиля (шлицевых, эвольвентных, многогранных). Наружные протяжки применяют для обработки плоскостей и фасонных поверхностей на призматических деталях, а также цилиндрических и фасонных поверхностей на деталях тел вращения.
По конструкции протяжки бывают цельные и сборные. По схемам резания они различаются на одинарные (обычные) и групповые
(протяжки переменного резания). Протяжки чаще всего делают
комбинированными, выполняющими черновую и чистовую окончательную обработку. Однако в некоторых случаях протяжки изготовляют только с режущими или только с калибрующими или выглаживающими зубьями. Первые удаляют основной припуск под протягивание. Вторые имеют несколько чистовых и калибрующих зубьев, которые окончательно обрабатывают отверстие.
Выглаживающие или уплотняющие протяжки пластически уплотняют поверхностный слой металла при получении низких пара-
метров шероховатости обработанной поверхности. Обычно их применяют для изготовления только круглых отверстий.
В работе протяжки испытывают растягивающие усилия. Если
инструмент этого класса работает на сжатие, то он называется прошивкой. Для обеспечения продольной устойчивости длина прошивки
не должна превышать 15 D. Прошивки по сравнению с протяжками
применяют редко.
Из всех разновидностей чаще всего применяют протяжки для
обработки круглых отверстий, поэтому ниже будут рассмотрены
основы проектирования именно этих протяжек. Основные положения проектирования круглых протяжек справедливы и для других
видов протяжных инструментов. Далее приведены особенности их
расчета и конструирования.
Протяжки для обработки круглых отверстий. Основными размерами цилиндрических отверстий, обрабатываемых протяжками, являются диаметр d = 5...80 мм, длина L = (3...5)·d. Основные части протяжки показаны на рис. 2.1.
Хвостовик служит для закрепления протяжки в патроне станка.
Хвостовик делается под патрон с клиновым креплением и под
быстродействующий патрон с автоматическим креплением. В хвостовике первой разновидности делается продолговатое отверстие,
в которое через патрон вставляют клин, удерживающий протяжку
в работе. Такое крепление неэффективно, поэтому его редко применяют на практике. Достоинством хвостовика с круговой выточкой
являются быстрота закрепления и раскрепления протяжки, простота
изготовления, достаточно высокая прочность.
Диаметр хвостовика d1= d0–(0,5...1), мм, где d0 – диаметр
предварительно подготовленного отверстия. Длина хвостовика l1 = (2...5)· d1, здесь меньший коэффициент принимается для больших протяжек. Диаметр выточки d' = (0,7...0,8)· d1 Указанные размеры хвостовика должны быть согласованы с нормализованными значениями диаметров в соответствии с имеющимся на станке патроном. Допуск на диаметр хвостовика обычно принимают по посадке f9.
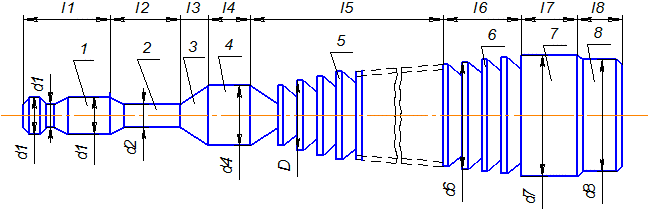
Рис. 2.1. Части цилиндрической протяжки:
1 – хвостовик; 2 – шейка; 3 – переходный конус; 4 – передняя направляющая часть; 5 – режущая часть; 6 – калибрующая часть; 7 – концевое направление; 8 – опорная цапфа (для длинных и тяжелых протяжек); 9 – центровое отверстие, которое является базой для изготовления и переточки протяжек
Для крепления шпоночных и подобных им протяжек применяют
призматические хвостовики, которые также выполняют под клиновое крепление и под кулачковые быстродействующие патроны (рис. 2.2).
При протягивании одного шпоночного паза или при одностороннем протягивании других поверхностей возникает внецентровое приложение нагрузки. Протяжка будет работать не только на растяжение, но и на изгиб. Для уменьшения изгибающего момента у призматических хвостовиков, показанных на рис. 2.2, б, в, паз необходимо располагать со стороны режущих зубьев протяжки. Хвостовик, показанный на рис. 2.2, а, сложнее в изготовлении, но имеет большую жесткость, и для случая протягивания двустороннего паза протяжка испытывает относительно меньшие напряжения, так как работает только на растяжение.
Шейка является вспомогательным элементом, связывающим хвостовик с направляющей и рабочей частями протяжки. Длина ее зависит от толщины стола и опорного кольца протяжного станка. Диаметр шейки d2 равен или на 0,5...1 мм меньше диаметра хвостовика. Обычно на ней маркируют протяжку.
Переходный конус облегчает направление детали или протяжки
в момент входа направляющей части в отверстие. Его шлифуют, длина l3= 10...25 мм с учетом диаметра протяжки.
Направляющая часть служит для центрирования обрабатываемого отверстия относительно оси протяжки, а также исключает перекос детали на протяжке.

Рис. 2.2. Призматические хвостовики
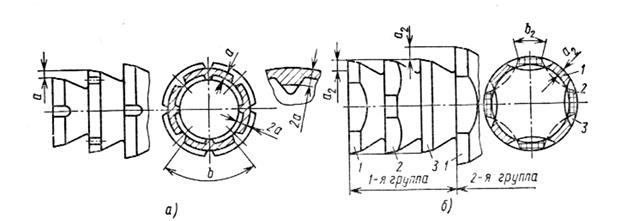
Рис. 2.3. Одинарная (а) переменная (б) схемы резания
Форма направляющей части должна соответствовать форме предварительно подготовленного отверстия. Диаметр направляющей части равен наименьшему диаметру подготовленного отверстия, т. е. d4 = d0 min. Допуск на погрешность изготовления принимается по посадке f7. Длину направляющей части делают равной от 0,75 до 1 длины обрабатываемого отверстия.
Режущая часть протяжки является основной, которая срезает
необходимый металл в заготовке. Она состоит из черновых, получистовых и чистовых зубьев. Режущая часть протяжки определяется
схемой протягивания, параметрами срезаемого слоя, конструктивными элементами и геометрическими параметрами зубьев, числом
зубьев и длиной.
Под схемой резания при протягивании понимают картину постепенного изменения формы и размеров обрабатываемого отверстия
или способ распределения работы между режущими зубьями протяжки. Существуют две схемы резания при протягивании: одинарная и групповая, или переменного резания.
Одинарная, или обычная, схема – это схема, когда каждый режущий зуб срезает широкий b, но тонкий а слой (рис. 2.3, а). В этом
случае диаметр или высота каждого последующего зуба режущей
части протяжки больше предыдущего на определенную, обычно
постоянную величину, равную 2·а или а.
Схема переменного резания такая, когда каждый режущий зуб
срезает короткий b2, но толстый слой а2. Режущая часть протяжки
конструируется так, что она состоит из нескольких групп зубьев
разного диаметра или разной высоты, а каждая группа имеет несколько зубьев (2...5) одного диаметра или одной высоты (рис. 2.3, б). Здесь цифрами 1...3 обозначены режущие зубья одной группы, лежащие на одном диаметре, кроме последнего, т. е. третьего. Срезаемые слои с параметрами а2 и b2 обозначены соответственно теми же цифрами.
Выкружки на зубьях делаются так, чтобы площадь, срезаемая
каждым зубом данной группы, была одинаковая. Последний зуб
третьей группы без выкружки, сплошной. Он срезает слои не сплошь
по всей окружности, а то, что осталось не срезанным первыми двумя
зубьями (на рисунке не заштрихованный слой). Его диаметр на 0,02...0,04 мм меньше диаметра предыдущих зубьев данной группы. Делается это для того, чтобы исключить резание зубом по всей длине окружности. Такое явление может возникать при уменьшении диаметра отверстия за счет упругих деформаций после прохода предыдущих зубьев этой группы.
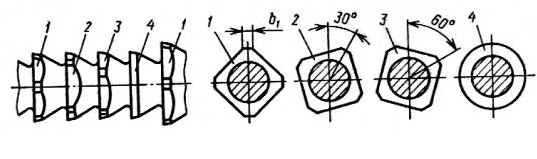
Рис. 2.4. Многогранные зубья групповой протяжки
Формообразование профиля отверстия по схеме переменного
резания производится последовательным или генераторным методом, при котором контур поверхности формируется по участкам последовательно режущими кромками различных зубьев.
При одинарной схеме резания поверхность образуется, как правило, методом подобия или профильным, когда контур режущей кромки каждого зуба подобен профилю окончательно обработанного отверстия (поверхности).
Чем больше число зубьев в группе, тем круговые вырезы получаются более длинными и глубокими. Когда число зубьев в группе больше трех, то выкружки можно заменить плоскостями. Тогда каждый зуб в группе, кроме последнего, будет представлять многогранник, повернутый относительно другого на некоторый угол (рис. 2.4). Для zр = 4 угол θ = 30°. Такие многогранные зубья легче изготовить, их плоскости шлифуются напроход. На последнем зубе группы лыска не снимается. Он остается круглым, но срезает площадь такую же, как и каждый предыдущий зуб данной группы.
В соответствии со схемами резания существуют также и протяжки одинарного резания и группового, или переменного, резания. Протяжки переменного резания имеют ряд преимуществ по сравнению с протяжками одинарного резания.
1. Чем больше толщина срезаемого слоя, тем меньше давление резания. Зависимость между толщиной срезаемого слоя и давлением резания показана на рис. 2.5. Давление резания р резко возрастает при толщине срезаемого слоя а < 0,025 мм. Такая толщина срезаемого слоя принимается при обработке отверстий из стали круглыми протяжками одинарного резания. Толщина срезаемого слоя протяжками переменного резания в несколько раз больше. Следовательно, давление резания будет значительно меньше, чем при работе протяжками одинарного резания.
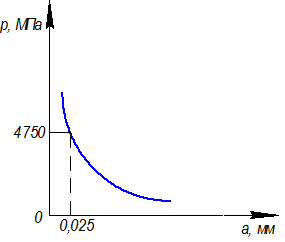
Рис. 2.5. Зависимость давления резания от толщины срезаемого слоя
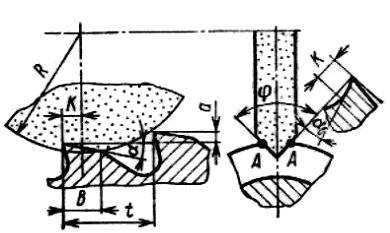
Рис. 2.6. Образование и геометрия стружкоразделительных канавок
При равной площади сечения срезаемого слоя протяжки переменного резания будут создавать меньшие силы резания, или при одинаковой силе ими можно срезать большую площадь. Конструктивно это
скажется на уменьшении числа режущих зубьев, а, следовательно, и длины протяжки.
2. Одинарные протяжки срезают тонкие слои, но большей ширины. При обработке отверстий образующуюся дугообразную стружку большей ширины трудно деформировать в кольцевой виток. Такой виток получается недостаточно плотным, он требует большего объема канавки для своего размещения. Поэтому увеличивается шаг между режущими зубьями протяжки, а следовательно, и ее длина.
Для лучшего свертывания стружки ее ширину уменьшают путем
прорезания на режущих кромках стружкоразделительных канавок,
которые располагаются на соседних зубьях в шахматном порядке.
Но в этом случае возникает определенный недостаток: канавки предыдущего зуба не срезают металл. В этом месте режущие кромки последующего зуба срезают двойную толщину слоя (см. рис. 2.3). В результате у укороченной, но дугообразной стружки создается ребро жесткости, которое затрудняет ее свертывание в плотный виток или спираль.
Протяжки переменного резания этого недостатка почти не имеют.
Короткая прямая стружка, имеющая большую, но постоянную толщину, равномерно деформируется при завивании и более плотно укладывается во впадине между зубьями. От этого относительная длина шага между режущими зубьями и длина режущей части протяжки уменьшаются на 30 % [2].
3. Стружкоразделительные канавки у протяжек одинарного резания наряду с положительными их функциями имеют существенный недостаток. Их прорезают дисковым кругом, ось которого перпендикулярна к оси протяжки. Протяжку в центрах устанавливают так, чтобы образовать задний угол на дне канавки, равный заднему углу на вершине зубьев. Для цельных круглых протяжек он обычно принимается 2 – 3-й. В результате режущая кромка получается ломаной, ослабленной массивностью угловых участков (рис. 2.6).
В окрестности точек А создается повышенная тепловая напряженность, что ведет к более интенсивному изнашиванию зубьев. Кроме того, боковые задние углы α6 вспомогательных режущих кромок получаются очень малыми tgα6 = tgα· sinφ/2, что также способствует более интенсивному изнашиванию угловых режущих кромок. Для уменьшения этого отрицательного влияния угол профиля абразивного круга φ для канавок необходимо принимать не менее 90...100°.
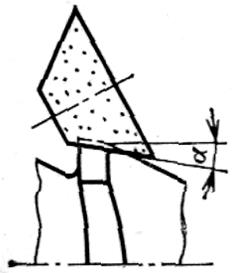
Рис. 2.7. Образование выкружки
Для правильного образования канавок по всей ширине зуба протяжки размер К должен быть равен размеру В. В ряде случаев это сделать невозможно, так как круг может коснуться и срезать кромку следующего зуба. Когда К < В, то начиная от оси круга вправо в канавках создаются отрицательные задние углы по всему контуру. Это еще больше усиливает отрицательное влияние стружкоразделительных канавок на режущие свойства протяжек. На практике условия правильного образования канавок не всегда соблюдаются. Угол φ берется меньше 900, шлифовальный круг быстро осыпается и теряет необходимую форму, правится он вручную с полукруглым'
профилем. В результате даже у новых (непереточенных) протяжек
боковые задние углы в точке А равны нулю или близки к этому.
Протяжки переменного резания почти не имеют этих недостатков. Массивность вершин зубьев у них больше. У многогранных зубьев задние углы по всему контуру равны а, а зубья с выкружками затачиваются по задней поверхности так, как показано на рис. 2.7. Здесь ось конического круга и ось протяжки лежат в одной плоскости. Боковые задние углы на выкружке получаются почти такими же, как и основной задний угол α = 3...4°. В результате стойкость протяжек группового резания получается в 2 раза выше стойкости протяжек одинарного резания.
4. Толщина срезаемого слоя протяжками переменного резания
в 5...8 раз больше толщины срезаемого слоя протяжками одинарного
резания. Поэтому ими можно в ряде случаев обрабатывать отверстия, полученные после литья, ковки или штамповки. При этом режущие
кромки не будут работать по корке вследствие большой толщины
среза.
Благодаря перечисленным преимуществам протяжки переменного
резания являются более прогрессивными инструментами и все!
больше применяются в машиностроении, Итак, схемы резания определяют основные конструктивные параметры режущей части; диа-1
метр зубьев протяжки, число и шаг зубьев.
Диаметр (высота) режущих зубьев. Режущая часть состоит из
черновых, получистовых и чистовых зубьев. Для протяжек одинарного резания первый режущий зуб делается по форме подготовленного отверстия. Диаметр (высота) первого зуба равен номинальному диаметру (высоте) предварительно подготовленного отверстия (поверхности), т. е. D1 < d0. Диаметр первой группы зубьев у протяжек переменного резания D1= d0 + 0,5аг. Диаметр каждого последующего чернового зуба или группы черновых зубьев будет увеличиваться на две толщины срезаемого слоя для двусторонних протяжек, или высота каждого последующего зуба будет увеличиваться на одну
толщину срезаемого слоя для односторонних протяжек (типа шпоночных).
Так, для двусторонних протяжек
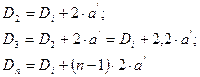
для односторонних протяжек

где а' = а – толщина срезаемого слоя для протяжек одинарного резания; а' = аг – толщина для протяжек переменного резания; Н1, Н2, Н h – высота зуба соответственно шпоночной или другой призматической протяжки, измеряемая от ее опорной плоскости.
Для устранения неровностей и других дефектов поверхностной
деформации, оставшихся после черновых зубьев, а также для более
плавного перехода режущих зубьев к калибрующим и для повышения равномерности протягивания после черновых выполняют получистовые и чистовые зубья или группы зубьев.
У протяжек одинарного резания число таких переходных зубьев
принимается от 2 до 5 в зависимости от формы, точности и шероховатости поверхности обработанного отверстия.
Большее число получистовых и чистовых зубьев делается для
обработки круглых отверстий.
Переходными зубьями удаляется припуск, равный толщине слоя,
срезаемого черновым зубом протяжки. Толщина срезаемого слоя
каждым переходным зубом уменьшается от первого к последнему.
Если рассмотреть три переходных зуба, то первый — получистовой срезает слой шириной а1 = 0,5·а, второй – чистовой – а2 = 0,3·а, третий – чистовой – а3 = 0,2а.
При этом минимальная толщина слоя, срезаемая последним
чистовым зубом а 3, должна быть не менее 0,008...0,01 мм. При
меньших толщинах вследствие наличия радиуса скругления режу-
щей кромки слой режущей кромкой не срезается, а подминается и
вдавливается в обрабатываемую поверхность.
В соответствии с этим будут увеличиваться и диаметры или высоты получистового и чистовых зубьев. Диаметр последнего чистового зуба D = dmax при протягивании отверстий в вязких металлах тонкостенных деталей, когда происходит усадка отверстия, и D = dmax – 0,3·δ при протягивании отверстий в толстостенных Деталях, для которых наблюдается разбивка отверстия, где dmax – наибольший диаметр протягиваемого отверстия; δ – допуск на изготовление отверстия.
Диаметр последнего чистового зуба можно принимать равным
номинальному диаметру обрабатываемого отверстия. Тогда усадка
или разбивка отверстия, а также допуск на погрешность его изготовления будут восприниматься и корректироваться калибрующими зубьями. На получистовых и чистовых зубьях стружко-разделительные канавки не делают.
Для протяжек группового резания обычно одну-две секции
выполняют получистовыми и одну-две секции, или три-пять зубьев,
чистовыми. Припуск на все переходные зубья принимается также равным толщине срезаемого слоя одной группой черновых зубьев. Первая получистовая секция или группа зубьев срезает толщину, равную 0,6·аг. Она имеет столько же зубьев, сколько их в каждой черновой группе. Обычно число чистовых зубьев в группе равно количеству черновых. Они также имеют выкружки, но диаметр их в группе одинаковый. Если же чистовые зубья выполнены кольцевыми, то они работают по одинарной схеме резания. Толщины срезаемого слоя каждым чистовым зубом, и их диаметры или высотные размеры определяются так же, как для чистовых зубьев одинарных протяжек. Стружкоразделительных канавок на них также нет.
Число черновых зубьев для протяжек одинарного резания
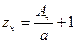 2.1
2.1
где Ач – припуск на сторону, оставляемый под черновые зубья; Ач = А – A1 здесь А – общий припуск на сторону под протягивание; А i – припуск на сторону, оставляемый под чистовые зубья. Как указывалось ранее, А1=а. Единица в формулу (2.1) добавляется потому, что первый зуб протяжек одинарного резания номинально не работает, его размер равен размеру предварительно подготовленного отверстия (поверхности).
В отличие от протяжек одинарного резания для групповых протяжек первая секция зубьев снимает половину толщины срезаемого
слоя, т. е. 0,5аг. Поэтому для протяжек переменного резания число
черновых зубьев

здесь 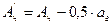 2.2
2.2
Тогда 
где zг – число зубьев в каждой группе; аг – толщина слоя, срезаемого каждой группой зубьев; А'ч – припуск на сторону, срезаемый черновыми зубьями без первой группы зубьев.
Отношение Ач/аг = n, т.е. равно числу черновых групп протяжки. Число получистовых и чистовых зубьев, как указывалось ранее,
для протяжек одинарного резания zl = 2...5, а для протяжек переменного резания z1 = z г + (3...5).
Припуск под протягивание определяется профилем отверстия
или поверхности и зависит от их размеров. Он на основании экспериментальных исследований и производственного опыта определяется по нормативным таблицам НИИТавтопрома или по эмпирическим формулам. Для протяжек одинарного и переменного резания припуск одинаковый. Для круглых отверстий припуск под протягивание на диаметр (рис. 2.8) можно рассчитывать по уравнениям:
при подготовке отверстия сверлом
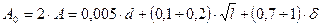 2.3
2.3
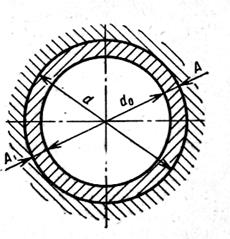
Рис. 2.8. Припуск под протягивание
при подготовке отверстия зенкерованием или растачиванием
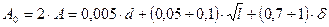 2.4
2.4
где А0 – припуск под протягивание на диаметр; d – минимальный диаметр
обрабатываемого отверстия; l – длина протягиваемого отверстия; δ – допуск на изготовление отверстия.
Для шпоночных и шлицевых пазов, а также для многогранных
отверстий к найденному припуску по формулам (2.3) и (2.4) необходимо добавлять высоту пазов и высоту угловых элементов. Тогда диаметр отверстия, подготовленного под протягивание, d0 = dmax – А0, где dmax – d + (0,7...1) δ.
Толщина срезаемого слоя для протяжек одинарного резания
принимается небольшая. Она зависит от вида протяжек или протягиваемого отверстия и от обрабатываемого материала. В табл. 2.1 приведены толщины срезаемого слоя при обработке протяжками одинарного резания для наиболее употребительных типов протяжек и обрабатываемых материалов[3].
Толщина срезаемого слоя менее 0,010 – 0,015 мм нежелательна,
гак как она становится соизмеримой с радиусом скругления режу-
щей кромки зуба. В этом случае процесс резания затрудняется,
режущая кромка не захватывает такую малую толщину слоя, кото-
рый подминается задней поверхностью и вдавливается в заготовку.
Обработанная поверхность упрочняется, получается наклепанной.
Вследствие этого давление резания резко возрастает, и при малых
значениях задних углов происходит интенсивное изнашивание
зубьев инструмента.
Большие значения толщины срезаемого слоя ограничиваются
илами резания, условиями размещения стружки во впадине между
зубьями, прочностью протяжки и качеством обработанной поверх-
ности.
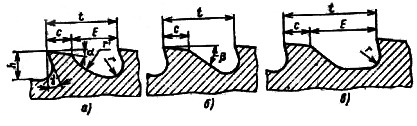
Рис. 2.9. Элементы зубьев и канавок протяжки
Таблица 2.1.
Толщина срезаемого слоя при протягивании, мм
Протяжка
Обрабатываемый материал
Чугун
0,015 – 0,04
0,03 – 0,01
0,03 – 0,15
0,05 – 0,12
Для протяжек переменного резания толщина срезаемого слоя значительно больше, чем для протяжек одинарного резания. Она
составляет 0,3...0,4 мм при обработке сталей и 1,0...1,2 мм при
обработке чугуна. Объясняется это тем, что срезаемый слой короткий, стружка почти прямая, относительно легче деформируется и •
более плотно укладывается во впадине между зубьями. Этому способствует и лучшая геометрия режущих зубьев у протяжек переменного резания.
Шаг и стружечные канавки между зубьями. На выбор шага влияют
два противоречивых направления. С одной стороны, желательно проектировать протяжки с наименьшим шагом. Чем меньше шаг, тем короче протяжка и ниже ее стоимость, больше число зубьев одновременно участвующих в работе, и выше плавность процесса протягивания, повышается производительность и качество обработанной поверхности.
С другой стороны, чем меньше шаг, тем больше сила протягивания и возникает опасность разрыва самой протяжки, тем меньше
толщина зуба и пространство для размещения стружки. Отсюда видно, что на шаг влияет большое число факторов, которые учесть весьма трудно. Поэтому предварительно шаг зубьев определяют по формулам:
для протяжек одинарного резания
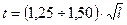 2.5
2.5
для протяжек группового резания
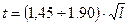 2.6
2.6
где l – длина обрабатываемого отверстия.
Затем в зависимости от шага определяются другие элементы зуба
и основные размеры стружечной канавки (рис. 2.9): толщина зуба
с = (0,30...0,35)· t; высота зуба или глубина канавки h = (0,35...0,45)· t радиус дна канавки r = 0,5· h или r = (0,18...0,22)· t; ширина канавки Е = (0,65...0,7)· t; радиус спинки зуба, если она вогнутая, r' = (0,65...0,7)· t.
Вогнутую спинку зуба (рис. 2.9,а) делают у протяжек для обработки вязких материалов, когда образуется сливная стружка, требующая большого объема для осевого размещения. Для таких материалов принимается и больший коэффициент при определении глубины канавки h в целях увеличения ее объема.
Для обработки хрупких материалов спинку зуба делают прв
нелинейной (рис. 2.9, б). В этом случае образуется элементная стружка, которая более равномерно и полнее заполняет канавку. Поэтому она может иметь относительно меньший объем

Рис. 2.10. Схема расчетной площади канавки
При обработке длинных отверстий шаг зубьев получается сравнительно большим, объем срезаемого слоя увеличивается. Поэтому
для увеличения объема стружечных канавок их дно рекомендуется
делать с прямолинейным участком (рис.2.9,в). Относительная толщина зуба для них уменьшается с = (0,2...0,25)· t. Прямолинейная спинка зуба имеет угол наклона β = 50...55°.
Более правильно элементы зубьев и канавок определять с учетом не только длины протягиваемого отверстия, но и толщины срезаемого слоя, а также объемного коэффициента стружки. При расчете учитывается нормальное, свободное размещение стружки в объеме или в площади активной части канавки.
Как показано на рис. 2.10, площадь активной части канавки
принимается равной площади окружности радиуса r или диаметра h,
т. е. Fк = π h2/4.
Дополнительная площадь канавки Fдоп составляет 25...30% общей площади канавки. Она является как бы резервной; при нормальном размещении сливной стружки она почти не участвует в работе. Площадь, занимаемая стружкой, Fc = FK. Площадь осевого сечения слоя металла, срезаемого одним зубом протяжки,
Fм = a · l .
Отношение площади объема, занимаемой стружкой, к площади
осевого сечения (объему) срезаемого слоя называется коэффициентом
заполнения стружечной канавки, или объемным коэффициентом стружки, т. е.
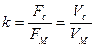 ,
, 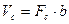 , а
, а  .
.
Откуда 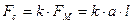 .
.  , получим
, получим
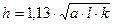 2.7
2.7
Уравнение (2.7) справедливо для обработки вязких металлов,
когда образуется сливная стружка.
При обработке хрупких материалов образуется элементная
стружка, которая более равномерно заполняет почти весь объем
канавки. При такой обработке площадь канавки может быть меньше
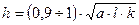 2.8
2.8
Коэффициент заполнения стружечной канавки, или объемный
коэффициент стружки, определяется экспериментальным путем. Он за-
висит от толщины срезаемого слоя и обрабатываемого материала. Его
значение всегда больше единицы и изменяется от 2 до 5 в зависимости
от указанных условий обработки. Так, для протяжек одинарного резания k = 2,5...5, для протяжек группового резания к = 2...3,5. Причем, чем меньше толщина срезаемого слоя а и чем более вязкий обрабатываемый материал, тем больше коэффициент k .
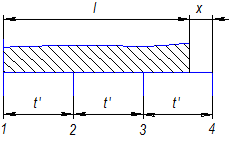
Рис. 4.11. Положение зубьев протяжки относительно поверхности детали
Все элементы зуба и канавки определяются в зависимости от h
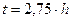 ;
; 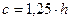 ;
;  ;
; 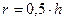 ;
; 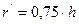 2.9
2.9
Этот способ расчета позволяет более правильно определить
площадь или объем стружечной канавки, не завышать ее размеры,
вследствие чего уменьшается шаг t и длина режущей части протяжки.
Определив шаг, необходимо проверить, чтобы число зубьев,
одновременно участвующих в работе, было не менее двух
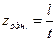 2.10
2.10
Чаще всего это отношение – целое число с десятыми долями.
По времени оно означает усредненное число зубьев, одновременно участвующих в работе. Например, если zодн=3,5, то половину
определенного времени работают три зуба, а половину – четыре зуба. Таким образом, в действительности в каждый момент времени
одновременно работает целое число зубьев. Если учитывать только
номинальный размер шага без допуска, то всегда разница между максимальным и минимальным числом зубьев, одновременно находящихся в работе,
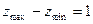 2.11
2.11
Для повышения плавности процесса протягивания лучше, когда
Zmin = 3...4. При обработке длинных отверстий число одновременно работающих зубьев может достигать 7...8, если это допускается
прочностью протяжки и тяговой силой протяжного станка. Во всех
случаях процесс протягивания является неравномерным, силы резания не остаются постоянными, так как число одновременно работающих зубьев изменяется на единицу.
Для повышения плавности процесса протягивания расчетный шаг необходимо корректировать.
Целесообразно расчетный шаг t сделать равным t', подчинив
его условию, по которому при выходе очередного зуба из детали
входящий зуб должен отстоять от торца детали на расстояние х = 0,1· t' (рис. 2.11). Тогда t'· Zmax = l + 0,1· t'. Откуда
 , 2.12
, 2.12
где Zmax = ( l/ t)+1
Качество поверхности в основном определяется работой чистовых зубьев протяжки. Для устранения волнистости обработанной поверхности шаг чистовых зубьев делается переменным. Номинальное значение шага чистовых зубьев принимают равным шагу черновых зубьев или же уменьшенным примерно на 0,25. Шаг между первым и вторым чистовым зубом принимается равным номинальному, между последующими зубьями на 5...10 % меньше.
Геометрия режущих зубьев. Передний угол зубьев протяжек
в основном зависит от качества обрабатываемого материала. Для
обработки сталей он принимается 12...18°, чугуна γ = 5...10°, для
вязких цветных металлов и сплавов γ = 25°.
Переточку протяжек по мере изнашивания зубьев производят
по передней поверхности. При небольших значениях заднего угла этим
достигается незначительное изменение диаметра или высоты зубьев
и увеличение срока службы протяжки. Для сохранения диаметральных или высотных размеров после переточки задние углы у зубьев многих видов протяжек принимаются малыми. Так, для внутренних протяжек α = 2...30 при обработке отверстий 6-го квалитета точности, α = 3...40 при обработке отверстий меньшей точности. Для шпоночных и наружных нерегулируемых протяжек α = 4...70. Для наружных протяжек сборной конструкции с зубьями, регулируемыми по высоте, задний угол α = 8...120.
Как указывалось ранее, для лучшей деформации стружки, т. е.
для более плотного ее завивания и размещения во впадине, на черновых зубьях у протяжек одинарного резания при обработке вязких металлов делают стружкоразделительные канавки (см. рис. 2.6). Их располагают в шахматном порядке на последующем зубе на расстоянии 8...12 мм. Па переходных режущих зубьях, т. е. на получистовых и чистовых, стружкоразделительные канавки не выполняют.
Калибрующая часть протяжек имеет несколько зубьев, которые
придают поверхности или отверстию окончательную точность и
шероховатость. Теоретически калибрующие зубья не режут, так
как они не имеют подъема на зуб. Практически первый калибрующий
зуб может срезать весьма тонкие стружки за счет его некоторого
превышения над размером последнего чистового режущего зуба.
По мере изнашивания протяжки получистовые и чистовые зубья
постепенно переводят в черновые, а калибрующие зубья – в режущие чистовые.
Число калибрующих зубьев зависит от точности обработки и
принимается от 2 до 7. С повышением точности обработки число
калибрующих зубьев увеличивается.
Шаг калибрующих зубьев принимается такой же, как и у режущих, если обработка ведется по 11-му и более низкому квалитету
точности. Для изделий 7...9-го квалитета точности t к = 0,75· t '. Шаг калибрующих зубьев неравномерный, так же как у чистовых
зубьев. Передний угол у калибрующих зубьев обычно берется таким же, как у черновых. Однако для более точных протяжек передний угол рекомендуется делать значительно меньше (для стали 50 и для чугуна 00).
В целях повышения размерной стойкости протяжек задний угол
калибрующих зубьев меньше, чем режущих. Для внутренних протяжек у калибрующих зубьев α = 0,5...10, для шпоночных и наружных α = 1,5...20, для протяжек с регулируемыми зубьями α = 3...40. Для внутренних протяжек диаметр калибрующих зубьев такой же, как у последнего чистового режущего зуба.
В более общем случае на практике диаметр калибрующих зубьев принимают равным наибольшему диаметру обработанного отверстия. Окончательно диаметр устанавливается опытным путем после»
первого пробного протягивания отверстия. Затем размер калибрующих зубьев доводится до необходимого. Допуск на изготовление калибрующей части внутренних протяжек δИ берется по системе вала. При этом для обработки отверстий 7 – 9-го квалитета точности δИ = h5, для отверстий 11-го и больших квалитетов точности δи = hв или δи = (1/4...1/5)·δ.
Концевое направление не допускает перекоса обработанной детали в момент выхода из нее последних калибрующих зубьев протяжки и тем самым устраняет повреждение обработанной поверхности и поломку зубьев инструмента. Форма концевого направления может не соответствовать профилю обработанного отверстия. Так, концевое направление может быть цилиндрическим не только для круглого, но и для квадратного, многогранного и шлицевого отверстия. У одношпоночных и наружных протяжек нет концевого направления. Длина концевой направляющей части l7 = (0,5...0,75)·l, но не более 60...70 мм. Диаметр концевого направления равен но-
минальному диаметру обрабатываемого отверстия, допуск на изготовление выполняется по посадке f7.
Для длинных и тяжелых протяжек, работающих на горизонтально-протяжных станках, за концевой направляющей делается цапфа, которая в скользящем люнете поддерживает протяжку от провисания.
Выглаживающие зубья. Для обработки круглых отверстий высокой точности и низкой шероховатости, от которых требуется повышенная износостойкость, применяют комбинированные протяжки, которые имеют еще и выглаживающие зубья (как правило, из твердого сплава). Их в виде колец или общего блока насаживают на цилиндрическую выточку протяжки и располагают за концевым направлением.
Число выглаживающих зубьев выбирают от 1 до 5 в зависимости от точности, шероховатости отверстия и качества обрабатываемого
материала. Выглаживающие зубья сферические или двусторонне
конические с цилиндрическим пояском посередине. Они не режут, а уплотняют поверхностный слой вследствие пластического деформирования, в результате чего повышается износостойкость детали.
Припуск на диаметр под выглаживающую часть протяжки небольшой 0,05...0,1 мм. Он распределяется между зубьями неравномерно. От первого выглаживающего зуба до последнего натяга т. е. толщина деформируемого слоя, уменьшается. Диаметр последнего выглаживающего зуба берется по максимальному размеру заданного отверстия. Затем после пробного прохода он доводится до нужного диаметра.
При наличии выглаживающей части протяжки диаметр чистовых и калибрующих зубьев уменьшается на величину натяга, оставляемого под выглаживание. Шаг выглаживающих зубьев такой же, как и калибрующих. После выглаживающих зубьев также делается концевое направление, но более короткое, чем после калибрующих зубьев. Оно тоже насадное и закрепляется в конце протяжки гайкой.
ПРОЧНОСТЬ ПРОТЯЖЕК
Протяжки работают на растяжение, поэтому их рассчитывают
па прочность при растяжении от основной составляющей силы резания Р, направленной вдоль оси протяжки. Условие прочности
протяжки выполняется, если
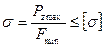 2.13
2.13
где σ – нормальные напряжения, возникающие в опасном сечении протяжки; Pzmax – наибольшая сила резания при протягивании; Fmin – наименьшая площадь поперечного сечения протяжки; [σ] – допускаемое напряжение на разрыв. Сила резания при протягивании
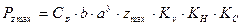 , 2.14
, 2.14
где Ср – коэффициент, зависящий от обрабатываемого материала
и формы протяжки; b – ширина срезаемого слоя, равная длине
периметра или длине окружности чернового режущего зуба, имею-
щего наибольший диаметр; а – толщина срезаемого слоя; у – пока-
затель степени; zmax – максимальное число зубьев, одновременно находящихся в работе, zmax = ( l/ t') + 1; К γ, Ки, Kс – поправочные коэффициенты соответственно на передний угол, на изнашивание зубьев и на СОЖ.
Коэффициент Ср представляет собой единичную силу, приходящуюся на 1 мм2 площади сечения срезаемого слоя. Давление резания зависит и от толщины срезаемого слоя а. Чем меньше толщина
срезаемого слоя, тем больше давление резания. Зависимость давления резания от толщины срезаемого слоя при протягивании по-
казана на рис. 2.5.
Значения коэффициента Ср и показателя степени у приведены
в табл. 2.2.
Поправочные коэффициенты для измененных условий резания
можно принимать следующие; К γ = 1, если γ = 100. Изменение
переднего угла на 10 приводит к изменению силы резания на 1...1,5%.
Для острых протяжек Ки = 1 и для затупившихся Ки = 1,15. При обработке сталей Кс = 1, если применяется сульфофрезол или эмульсия; Кс = 0,9, если применяется растительное масло.
Таблица 2.2.
Значение коэффициента Ср при протягивании
| Обрабатываемый материал | σ, МПа, или НВ | Коэффициент Ср, МПа, для протяжек | ??? | ||
| Шпоночных и пазовых | шлицевых | круглых | |||
| Сталь углеродистая конструкционная | До 700 700 – 800 Св. 800 | 1770 2020 2500 | 2120 2300 2840 | 7000 7620 8420 | 0,85 |
| Сталь легированная конструкционная | До 700 700 – 800 Св. 800 | 2020 2500 2820 | 2300 2840 3150 | 7620 8420 10000 | 0,85 |
| Чугун серый | HB ≤ 200 HB > 200 | 1150 1370 | 1250 1500 | 3000 3540 | 0,73 |
При обработке чугуна Кс = 0,9 для эмульсии и Кс = 1 без смазывания и охлаждения.
Наибольшая сила резания при протягивании должна быть равна
или меньше тягового усилия Q протяжного станка, а точнее, чтобы
не вызывать перегрузки станка Р zmaz = (0,8...0,9)· Q. Опасным у протяжек является то поперечное сечение, которое имеет наименьшую площадь (с учетом материала инструмента). Это шейка хвостовика под патрон или же сечение во впадине перед первым режущим зубом. В первом случае
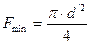 мм2, 2.15
мм2, 2.15
во втором
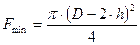 мм2 2.16
мм2 2.16
Допускаемое напряжение следует принимать [σ] = 200 МПа для хвостовика, если он сделан из сталей 45 и 40Х и сварен встык с рабочей частью протяжки; [σ] = 250 МПа для протяжек из стали ХВГ; [σ] = 350...400 МПа для протяжек из быстрорежущих сталей.
Если спроектированная протяжка не удовлетворяет условиям
прочности, необходимо увеличить шаг зубьев или уменьшить толщину срезаемого слоя, т. е. уменьшить Р zmax и провести поверочный расчет на прочность при измененных условиях.
Исходные данные
Чертеж детали, марка материала заготовки, твердость HB, предел прочности на растяжение sв, диаметр отверстия после протягивания D, длина протягиваемого отверстия L0 и шероховатость обрабатываемой поверхности.
Марка стали
Допустимое напряжение
Во всех случаях величина допуска на неточность изготовления должна быть в пределах 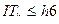
При обработке отверстий с большими допусками (I0 квалитет и грубее) определяется диаметр калибрующих зубьев


Рис.2.1.7 Схема работы и размеры калибрующих зубьев.
Примечание: 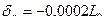 – величина разбивания отверстия при обработке цветных металлов и сплавов, где L0 - длина отверстия, мм;
– величина разбивания отверстия при обработке цветных металлов и сплавов, где L0 - длина отверстия, мм;
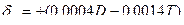 - величина усадки отверстия при обработке деталей типа втулок, вкладышей и углеродистых сталей;
- величина усадки отверстия при обработке деталей типа втулок, вкладышей и углеродистых сталей;
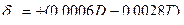 - то же – из легированных сталей, где D – диаметр протягиваемого отверстия, мм; T – толщина стенки отверстия, мм.
- то же – из легированных сталей, где D – диаметр протягиваемого отверстия, мм; T – толщина стенки отверстия, мм.
Допуск ITk на изготовление калибрующих зубьев протяжки определяется по формуле

где ITD - допуск на отверстие после протягивания.
Затем ITk уточняется по табл.2..
Число режущих зубьев
Число режущих зубьев определяется по формуле

где A1 - припуск на сторону; 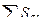 - суммарный подъем на зачищающие зубья; SZ - подача на режущий зуб.
- суммарный подъем на зачищающие зубья; SZ - подача на режущий зуб.
Число режущих зубьев уточняется при составлении таблицы размеров зубьев. Диаметр первого зуба найден ранее (см. рис.2.1.4), диаметр каждого последующего зуба увеличивается на величину 2SZ.
Наибольшее отклонение для размеров режущих зубьев назначается по табл. 2.1.13.
Учитывая, что диаметральный суммарный подъем на зачищающие зубья составляет 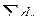 , получим размер первого калибрующего зуба по формуле
, получим размер первого калибрующего зуба по формуле
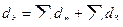
где 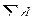 - диаметральный суммарный подъем на режущие зубья.
- диаметральный суммарный подъем на режущие зубья.
Значение 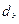 необходимо сопоставить со значением расчетной величины калибрующего зуба, найденной ранее (см.п.2.14). В случае их несоответствия необходимо увеличить или уменьшить
необходимо сопоставить со значением расчетной величины калибрующего зуба, найденной ранее (см.п.2.14). В случае их несоответствия необходимо увеличить или уменьшить  .
.
2.17. Число и размеры стружкоразделительных канавок для режущих зубьев.
Параметры канавок nk , Sk , hk , Rk определяют по табл.2.1.15.
2.18. Определение общей длины протяжки (см.рис.2.1.4)
Расстояние l от переднего торца протяжки до первого режущего зуба определяется как
l = l1 + l2 + lпш + l4 ,
где l1 - длина хвостовика, l1 определяется по табл.2.1.10; l2 – длина переходного конуса; lпш - длина переходной шейки; l4 - длина передней направляющей, l4 равна длине обрабатываемой заготовки
Длина lпш переходной шейки протяжки
lпш = l – ( l1 + l2 + l4).
Длина l2 переходного конуса назначается конструктивно от 5 до 20 мм, таким образом, чтобы угол конуса составлял 15...200.
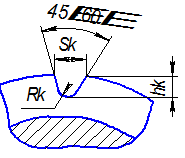
Таблица 2.1.15
Число и размеры стружкоделительных канавок для круглых протяжек
| Диаметр протяжки, мм | Количество канавок, nk | |||
Размеры канавок, мм
Длина режущей части протяжки
 .
.
Длина зачищающей и калибрующей частей протяжки
Общая длина протяжки
Ln = l + lp + lзк + l5 ,
где l5 = (0,5-0,7) L0 – длина задней направляющей протяжки, которая должна быть не менее 20 мм.
Отклонения общей длины протяжек.
3 мм – для протяжек длиной до 1000 мм.
5 мм – для протяжек длиной свыше 1000 мм.
2.19. Определение допустимого радиального биения на режущих зубьях протяжки.
Радиальное биение режущих зубьев протяжек  на 100 мм ее длины
на 100 мм ее длины
0,005 мм – у протяжек до 40Д,
0,006 мм – у протяжек длиной свыше 40Д.
2.2. Числовой пример расчета круглой протяжки
Исходные данные.
Материал: сталь 45; 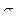 = 650 МПа; НВ 165 – 185;
= 650 МПа; НВ 165 – 185; 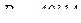 ; D =30Н8;
; D =30Н8;
L0 = 30 h14. (рис.5)
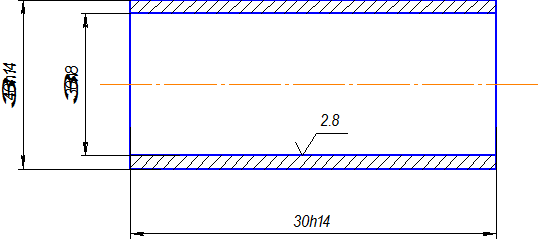
Рис.2.1.8. Чертеж детали
Число режущих зубьев
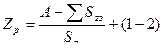
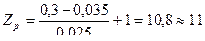 зубьев
зубьев
Составим таблицу режущих зубьев и уточним их число. Диаметр первого зуба определен ранее (см. п. 2.20.14)

dp4 = 29,56 мм; dp5 = 29,61 мм; dp6 = 29,66 мм;
dp7 = 29,71 мм; dp8 = 29,76 мм; dp9 = 29,81 мм;
dp10 = 29,86 мм; dp11 = 29,91 мм.
Наибольшее отклонение для режущих зубьев ITp = – 0,01 (согласно табл.2.1.14).
Учитывая, что  = 0,070 мм, получим диаметр калибрующих зубьев
= 0,070 мм, получим диаметр калибрующих зубьев
dk = 29,91+0,07=23,98 мм вместо расчетного dk = 30,03.
Следовательно, необходимо добавить один режущий зуб с диаметральным подъемом 0,05 мм, т.е.
dp12 = 29,91+0,05=29,96 мм.
III. ЧЕРВЯЧНЫЕ ФРЕЗЫ
Для обработки цилиндрических зубчатых колес методом обкатывания или огибания применяют различные инструменты: зуборезные гребенки и долбяки, червячные зуборезные фрезы, зуборезные головки, шеверы, дисковые и червячные шлифовальные круги. Метод обкатывания позволяет нарезать зубья колес непрерывно при их плавном вращении вокруг своих осей. Вследствие этого повышается производительность и точность обработки. Кроме того, одним инструментом данного модуля можно нарезать колеса с любым числом зубьев.
Основные параметры зубьев колес характеризуются размерами
исходного контура зубчатой рейки. Основные параметры зубьев
инструментов, работающих методом обкатывания, определяются
размерами контура инструментальной рейки.
Инструментальная рейка лежит в основе образования исходной и
производящей поверхностей. Параметры контура инструментальной
рейки отличаются от исходного контура рейки следующими элементами (рис. 3.1).
1. Высота ножки инструментальной рейки hfu (рис. 8.10, о)
больше высоты головки зубчатой рейки ha на (0,25...0,3) мм, где mn —
нормальный модуль зубьев колеса, мм. Это необходимо для того,
чтобы исключить из резания впадину инструментальной рейки, т. е.
наружный диаметр колеса инструментальной рейкой не обрабатывается.
2. Толщина зуба инструментальной рейки Su больше толщины
зуба зубчатой рейки S на Δ Su, где Su – π mn/2, Δ Su – увеличение
толщины зуба инструментальной рейки, необходимое для утонения
зуба нарезаемого колеса. Утонение зуба необходимо, чтобы обра-
зовать боковой зазор у сопряженных колес с фланкированными
зубьями. У нефланкированных колес этот зазор можно получить
смещением инструмента к центру колеса.
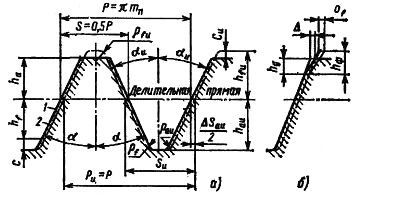
Рис. 3.1. Исходные контуры зубчатой 1 и инструментальной 2 реек
3. Для корригирования зубьев колес у зубчатой рейки делают
фланк, представляющий срез головки на величину hф (рис. 3.1.б)
под углом αф. В отличие от зубчатой рейки фланк инструментальной
рейки представляет собой утолщение ножки зуба, определяемое
высотой hф и углом αф u фланка. Обычно высота фланка hф u =
0,5 m, а угол αф u = 50.
Таким образом, размеры исходного контура инструментальной
рейки для некорригированного зубчатого зацепления, образованного
без смещения исходного контура, будут следующие: шаг между
зубьями Р nu=π· m; толщина зуба по средней (делительной) прямой Snu = (π m)/2 + Δ Su; высота зуба hu = hau + hfu = 1,25 mu + 1,25 mu = 2,5 mu; угол профиля α u = α0 – 20°; радиус закругления вершин зубьев и впадин r = (0,25...0,30) mu.
На рис. 3.1 показан исходный контур зубчатой и инструментальной реек и их параметры.
Зуборезные червячные фрезы
Червячные фрезы применяют для обработки прямозубых, косозубых и шевронных цилиндрических колес, а также для нарезания
зубьев червячных, колес с различными видами зацепления. Червяч-
ная фреза как инструмент получается из червяка путем прорезания
канавок, образующих переднюю поверхность зубьев и пространство
для размещения стружки и затылования зубьев для создания задних
углов по всему контуру.
По конструктивному выполнению червячные фрезы бывают цель-
ные, насадные и сборные. По виду обработки они подразделяются на
черновые (многозаходные), чистовые и прецизионные. По виду
исходного червяка, положенного в основу червячной фрезы, они бывают эвольвентные, архимедовы, конволютные для нарезания ко-
лес с эвольвентным зацеплением.
Для нарезания зубчатых колес о циклоидальным зацеплением и
с зацеплением Новикова применяют фрезы, в основу которых поло-
жены соответствующие червяки.
Червячные фрезы работают на специальных зубофрезерных
станках 5К301, 5К320, 5К32 и др., а также на тяжелых станках
5342, 5345, 5364, выпускаемых Коломенским станкостроительным
ПО. В процессе нарезания фреза и заготовка вращаются относительно
своих осей. За один оборот фрезы заготовка повернется на 1/ zк при
однозаходкой фрезе и на α/ zк, если фреза многозаходная; здесь zк – число зубьев нарезаемого колеса, α – число заходов фрезы. Кроме
того, станок имеет движение для врезания инструмента в радиальном
направлении к заготовке и движения суппорта для подачи. Подачу
осуществляют вдоль оси заготовки при обработке цилиндрических
колес; в радиальном направлении – при обработке червячных колес
или цилиндрических колес с узким ободом и в тангенциальном направ-
лении к заготовке – при нарезании червячных колес.
Метод зубофрезерования червячными фрезамн является высоко-
производительным и универсальным, получил широкое распростра-
нение во всех видах производства для обработки цилиндрических и
червячных колес. Обработку производят непрерывно, по методу
обкатки. В отличие от дисковых и пальцевых фрез одна червячная
фреза может обрабатывать колеса с любым числом зубьев данного
модуля. Недостатком метода зубофрезерования при осевой и радиаль-
ной подачах является ограниченность числа резцов, огибающих
профиль зубьев обрабатываемого колеса; вследствие этого шерохо-
ватость обработанной поверхности зубьев в ряде случаев высокая.
Число резов, профилирующих каждую боковую сторону зуба
изделия,
 , 3.1
, 3.1
где nпроф = l /Р0 – число витков фрезы, участвующих в профилиро-
вании (зацеплении); l – активная длина линии профилирования
(зацепления); Р0 – шаг между зубьями фрезы в направлении линии
профилирования, т. е. основной шаг; Zu – число зубьев фрезы. Длина
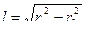 3.2
3.2
где ra и r0 – соответственно радиусы наружной и основной окруж-
ности нарезаемого колеса.
Чем больше число зубьев фрезы Zu и число зубьев колеса Zк, чем
меньше угол профиля зубьев фрезы, тем больше огибающих резов.
Величина огранки, мм, т. е. отклонения профиля от эвольвенты
у делительного диаметра при m = 1 мм, определяется по уравнению
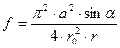 3.3
3.3
Кроме того, вследствие наличия продольной подачи S0 образующие
зубьев колеса получаются не прямолинейными, а волнистыми.
Волнистость, т. е. высота гребешков по дну впадины зуба, мм,
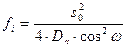 3.4
3.4
Волнистость по боковой стороне зуба, мм,
 3.5
3.5
где Da – нружный диаметр фрезы, мм; ω – угол наклона зуба
заготовки.
Конструктивные параметры фрезы. При проектировании зубо-
резных червячных фрез должны быть заданы некоторые параметры
зубчатого колеса: модуль т, угол давления на делительном диаметре,
т. е. угол зацепления α, высота зуба h и высота головки зуба ha
(рис. 3.2). Передний угол γв принимают для вершинных режущих
кромок и задний угол αв по наружному диаметру. Для стандартных
фрез γв = 0, αв = 10...12°.
В зависимости от вида и точности обработки колеса выбирают
также число заходов фрезы и класс ее точности. Для чистовой обра-
ботки применяют однозаходные фрезы, для черновой, предваритель-
ной – многозаходные.
Основными конструктивными параметрами червячной фрезы
являются диаметр, длина, диаметр отверстия под оправку, число
зубьев, форма и направление канавок, размеры профиля зубьев.
Наружный диаметр фрезы принимается по нормалям и стандартам
с учетом паспортных данных зубофрезерного станка, или же зада-
ются углом подъема витков исходного червяка и определяют делитель-
ный, а затем наружный диаметр фрезы.
При определении диаметра надо учитывать следующие противо-
речивые обстоятельства: с одной стороны, чем больше диаметр фрезы,
тем лучше, так как повышаются точность и производительность обра-
ботки; с другой стороны, с увеличением диаметра фрезы она стано-
вится дороже, увеличиваются крутящий момент и длина врезания
в заготовку. Для чистовых фрез рекомендуется принимать диаметр
больше, чем для черновых, а для прецизионных еще больше, чем для чистовых. ГОСТ 9324-80Е установил диаметры фрез общего назначе-
ния для m = l...25 мм от 71 до 305 мм.

Рис. 3.2. Конструктивные параметры червячной фрезы
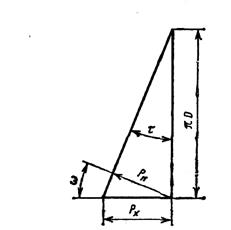
Рис. 3.3. К определению соотношения между D и τ
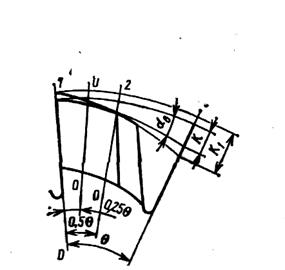
Рис. 3.4. Различные сечения зуба фрезы
При определении диаметра расчетным способом вначале задаются
углом подъема витков τ. Для чистовых фрез τ = 3...5°, для преци-
зионных его принимают до 3°.
Из рис. 3.3. видно, что при равенстве ω = τ

откуда делительный диаметр
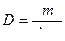 3.6
3.6
Наружный и внутренний диаметры
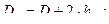
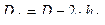 3.7
3.7
где hau, hfu – высота головки и ножки зубьев фрезы. Обычно они
равны 1,25·m...1,3·m.
По мере переточки зубьев по передней поверхности диаметры
фрезы уменьшаются вследствие наличия заднего угла. При этом будет
увеличиваться угол подъема винтовой линии τ и уменьшаться угол
наклона канавки ω на делительном диаметре фрезы. Вследствие этого
изменяется теоретически необходимый профиль зубьев. Действитель-
ный же профиль не меняется, остается постоянным при затыловании
резцом, когда образующими затылованных поверхностей являются
режущие кромки зубьев фрезы. При шлифовании затылованных
поверхностей действительный профиль зубьев по мере переточки
будет изменяться. В результате возникает погрешность профиля.
Чтобы уменьшилась эта погрешность, у червячных фрез расчетное
сечение 0 – 0 не должно совпадать с начальным сечением 1 – 0 для
новой фрезы. Она отстоит от него на (0,15...0,25)· Pz или на (0,15...0,25)·θ, где Pz и θ – оответственно окружной и угловой шаг между зубьями (канавками) фрезы
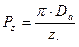 ,
,  3.8
3.8
где zu – число зубьев фрезы.
Указанные сечения показаны на рис. 3.4. Диаметры D и Da
найденные по уравнениям (3.7) и (3.8), относятся к расчетному
сечению. Если расчетное сечение отстоит от начального на 0,25·θ,
то для новой фрезы в сечении 1 – 0 D1 = D + 0,5 K, Da1 = Da + 0,5 K, Df1 = Df + 0,5·К.
В конечном сечении 2 – 0, соответствующем окончательно сточен-
ной фрезе (примерно на 2/3 толщины зуба) D2, Da2, Df2 по сравнению
с расчетными уменьшатся на 0,5· K.
Величина затылования для однозаходных фрез
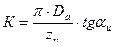
для многозаходных фрез, у которых большой угол τ,
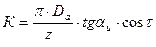
Диаметр отверстия под оправку можно рассчитать из условия
прочности и жесткости, затем расчетное значение подчинить нормаль-
ному ряду диаметров оправок по ГОСТ 9472-70. Ориентировочно
диаметр посадочного отверстия d = (0,20...0,45)· Da1.
Для повышения жесткости диаметр отверстия надо принимать по
возможности большим. После этого необходимо проверить, чтобы
расстояние между дном стружечной канавки и шпоночным пазом,
т.е. толщина стенки фрезы Т= Ra -( t 1 +Нк) или Т≥(0,25...
0,3)· d. Длина фрезы определяется так же, как шлицевой червячной
фрезы, т. е. L1 = l 1 + l '1 или
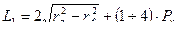 3.9
3.9
где ra, rf – радиус наружной и внутренней окружности колеса;
Р x – осевой шаг между зубьями фрезы; l1 – длина фрезы, находя-
щаяся в контакте с нарезаемым колесом; l'1 – удлинение, необходи-
мое для увеличения долговечности инструмента за счет осевых пере-
движек по мере изнашивания фрезы.
Ширина буртиков принимается 3...5 мм. Они служат для контроля
биения фрезы при изготовлении и установке ее на оправку шпинделя
зубофрезерного станка. Таким образом, общая длина фрезы L = L1 + 2 l. Диаметр буртиков D = (1,5... l,7)· d. Их делают на 1...2 мм ниже дна стружечной канавки.
Из уравнения (3.9) видно, что чем больше число зубьев и диаметр
нарезаемого колеса, тем больше длина фрезы. Например, для колеса
m = 5 мм, диаметром 5000 мм длина фрезы должна быть около 300 мм.
Длину фрезы можно уменьшить, если ее сделать с заборным конусом (рис.3.5).

Рис. 3.5. Червячная фреза с заборным конусом
В этом случае не только фреза становится короче (вместо l получается
длина l2), но и происходит перераспределение нагрузки на режущие зубья. При зубофрезеровании наибольшую площадь срезают зубья, входящие в работу. Делая заборный конус, мы более равномерно распределяем работу резания на другие зубья вдоль оси фрезы. Вследствие этого происходит более равномерное изнашивание инструмента. Длина заборного конуса lк делается 1,5...2 шага, а угол φк = 18...300.
Число зубьев фрезы должно быть по возможности наибольшим.
С увеличением zu увеличивается число резцов, уменьшается шерохо-
ватость поверхности, уменьшается толщина срезаемого слоя. Число
зубьев насадных цельных фрез ограничивается условиями затылова-
ния, а сборных – условиями крепления зубьев. Для червячных фрез
обычной точности принято zu = 12...9, для прецизионных zu =
= 16...12, для сборных затылованных zu = 10...8.
Канавки, образующие переднюю поверхность зубьев и простран-
ство для размещения стружки, могут быть винтовыми, перпендику-
лярными виткам зубьев фрезы на делительном диаметре в расчетном
сечении, и прямыми, проходящими через ось, если передний угол
γ = 0, или параллельными оси. если γ ≠ 0.
Стандартные фрезы изготовляют с канавками первого типа. Шаг
винтовой канавки PK = n· D· ctgω. Передние углы для левой и правой
режущих кромок у таких фрез получаются одинаковыми.
Фрезы с прямыми канавками проще в заточке, и изготовляемые
на основе архимедова червяка имеют меньшее теоретическое измене-
ние профиля при переточках. Однако передние углы для левой и пра-
вой режущей кромок у них разные. С одной стороны, в осевом на-
правлении γ0 = + τ, с другой стороны, γ0 = –τ . Поэтому фрезы с прямыми канавками делают с небольшими углами подъема витков
τ = 3...5°.
Глубина канавки для фрез с одним затылком
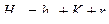
При двойном затыловании
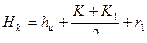
где hu – высота зуба фрезы, обычно hu = 2,5· m; К и К1 – величина
затылования шлифованной и нешлифованной части зуба, К1 = (1,25...
1,6)·К; r – радиус закругления дна канавки, обычно r = 1...3 мм.
Для фрез, имеющих модуль более 5 мм, как правило, делается
двойное затылование, так как из-за опасности срезания кругом режущей кромки следующего зуба при одинарном затыловании значительная часть зуба получается незатылованной. Поэтому первое затылование на величину К1 делают резцом до термообработки фрезы, а второе на величину К – шлифовальным кругом после термообработки. Считается нормальным, если длина шлифованного затылка равна 0,5· Pz, т. е. доходит до сечения фрезы 2 – 0. Угол канавки ε = 20...300.
Размеры профиля зубьев показаны на рис. 3.6. Для фрез,
профилируемых на основе конволютного червяка, профиль лежит
в нормальном сечении к виткам, и его размеры определяются в этом
сечении. Угол профиля таких фрез α u принимается равным углу
профиля α исходного контура зубчатой рейки.
Для фрез, профилируемых на основе архимедова червяка, профиль
задается в осевом сечении фрезы. Вследствие затылования боковых
поверхностей углы профиля для левой α u.л и правой α u.п стороны
у них будут разными.
Для некорригированного зацепления шаг между зубьями фрезы
в нормальном сечении Р n = π· m в осевом сечении Рх = Р n /со sτ.
Толщина зуба фрезы на делительной прямой

В ГОСТ 9324-80Е даны размеры зубьев фрез в нормальном сече-
нии, в котором учтено утолщение зубьев Δ S и приводятся допуски
на Sn в зависимости от модуля и классов точности червячных фрез.
Для m = 1...25 мм Δ S = 0,09...0,4 мм. Высота зуба фрезы
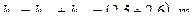
где ha. u – высота головки зуба фрезы, равная высоте ножки зуба
нарезаемого колеса, ha. u=(1,25...1,3)· mn; hf. u – высота ножки зуба
фрезы, hf. u= ha+ C· mn; ha – высота головки зуба колеса, равная
модулю mn; С – коэффициент радиального зазора передачи, обычно
С = 0,25...0,3.
Радиусы скругления вершины r1 и впадины r2, зубьев фрезы делают
в пределах высоты переходной кривой, а точнее, радиального зазора.
Для m=1 мм и более r1= r2=0,25...3 мм. Если для повышения
плавности зацепления головка зуба колеса несколько срезается, то
ножка зубьев фрезы фланкируется, утолщается. Размеры фланка hф=(0,45...0,5)· m, af = (0,005...0,02)· m.
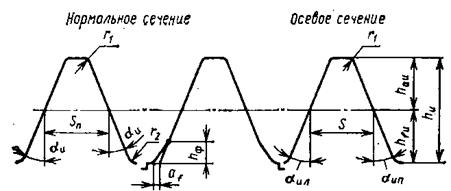
Рис. 3.6. Параметры профиля зубьев фрезы
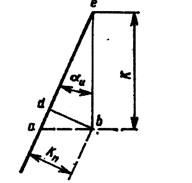
Рис. 3.7. К определению бокового заднего угла
Фланк может быть прямолинейным или вогнутым. У фрез с m > 5 мм для лучшего выхода шлифовального круга при затыловании профиля во впадине делаются канавки с размерами b1 и h1.
Геометрия зубьев фрезы. Стандартные червячные фрезы имеют
передний угол γ = 0 и задний угол по наружному диаметру α b = 10...120. Червячные фрезы могут проектироваться и изготовляться и с положительным передним углом γ b = 10...150. В сечении, нормальном к боковым режущим кромкам, задний и передний углы будут иными, значительно меньшими, чем для вершинной режущей кромки. На рис. 3.7 показана схема определения боковых задних углов в нормальном сечении. Из рисунка видно, что
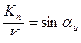 ;
; 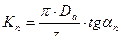 ;
; 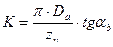
Разделив первое выражение на второе, получим

Аналогичное выражение можно получить и для переднего угла
в нормальном сечении к боковым режущим кромкам
 3.10
3.10
С учетом того, что поверхности винтовые, задний угол в нормаль-
ном сечении к боковым режущим кромкам
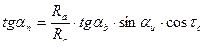 3.11
3.11
где Rc – радиус фрезы для рассматриваемой точки С; τс – угол
подъема винтовой линии на цилиндре радиуса Rc.
Анализ этих уравнений показывает, что на боковых режущих
кромках углы резания получаются недостаточными. Так, для фрезы,
у которой α u = 200, γв = 10°, αв = 10...12°, имеем γ n = 2° 30',
α n = 2' 30'...30.
Исходные данные
Параметры зубчатого колеса с эвольвентным профилем: модуль – m 0 число зубьев Z, угол зацепления d = 20°; ширина B , степень точности; угол наклона зуба  =0 (прямозубое колесо); марка материала зубчатого колеса.
=0 (прямозубое колесо); марка материала зубчатого колеса.
Оборудование – зубофрезерный станок.
3.1.2. Определение параметров исходной инструментальной рейки показано на рис. 3.1.1 (см.табл. 3.1.1).
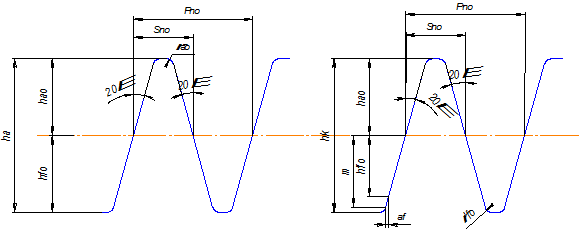
Рис 3.1.1. Профиль и параметры исходной инструментальной рейки:
а – с нефланкированным зубом; b – с фланкированным зубом; Р no - шаг по нормали между соседними профилями фрезы; Sno – толщина зуба фрезы по нормали к делителъной окружности; hu – высота зуба фрезы; hao – высота головки зуба фрезы; hfo – высота ножки зуба фрезы; 
 - радиус скругления вершины зубьев фрезы;
- радиус скругления вершины зубьев фрезы;  и
и 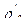 соответственно радиусы округления впадины зубьев фрезы с нефланкированным зубом, а с фланкированным; af - размер фланка.
соответственно радиусы округления впадины зубьев фрезы с нефланкированным зубом, а с фланкированным; af - размер фланка.
Основные параметры зубьев колес характеризуются размерами исходного контура зубчатой рейки. Параметры зубьев колеса (зубчатой гайки) определяются по следующим формулам: высота зуба h 0 =2,25m0; высота головки зуба h g =mо; толщина зуба по делительной линии Sg=0,5πm 0.
3.1.3. Расчетный профильный угол  , инструментальной рейки в нормальном сечении (профильный угол фрезы)
, инструментальной рейки в нормальном сечении (профильный угол фрезы)
Расчетный профильный угол  , инструментальной рейки в нормальном сечении (профильный угол фрезы) определяется исходя из характера зацепления. Для эвольвентного профиля
, инструментальной рейки в нормальном сечении (профильный угол фрезы) определяется исходя из характера зацепления. Для эвольвентного профиля 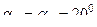
3.1.4. При нарезании прямозубого колеса (β=0) нормальный модуль mn. фрезы принимается равным модулю m0 колеса.
3.1.5. Шаг по нормали Р no, между соседними профилями фрезы (рис.1)
Pno = πmn .
3.1.6. Расчетная толщина зуба Sno фрезы по нормали к делительной окружности
Sno = Pno – ( Sg + 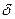 Sn 1 )
Sn 1 )
где 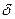 Sn 1 - припуск по толщине зуба под последующую обработку.
Sn 1 - припуск по толщине зуба под последующую обработку.
Осевой шаг фрезы
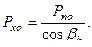
Исходные данные.
Зубчатое колесо с эвольвентным профилем. Угол наклона зубьев β = 0 (прямозубое колесо), mo = 2,5 мм; Z = 30;
В = 20 мм; степень точности колеса – 10; угол зацепления  = 20°. Материал колеса – бронза Бр АЖ-9-4. Оборудование: станок зубофрезерный мод. 5Д32.
= 20°. Материал колеса – бронза Бр АЖ-9-4. Оборудование: станок зубофрезерный мод. 5Д32.
Высота головки и ножки зуба
hao = hfo = ho – hg = 5.625 – 2,5 = 3,125.
Высота зуба фрезы
hu = hfo = ho – hg = 5,625 + 0,3 2,5 = 6,375 .
Выбор типа фрезы
Согласно ГОСТ 9324-80 и табл. 2, 3 для нарезания колеса 10 степени точности выбираем червячную однозаходную чистовую фрезу (класс С, тип 2).
Фрезу принимаем правозаходной. Основные размеры: dao = 71 мм; d = 27 мм; d1 = 40 мм; Ly = 63 мм; LN = 100 мм; Zo = 10 зубьев; l= 4 мм.
Угол контакта фрезы
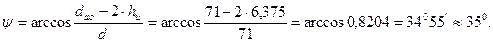
Число зубьев фрезы
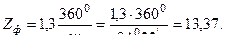
Уточняем число зубьев фрезы по ГОСТ 9324-80 (см. табл.3.1.3) Z ф =10.
Падение затылка
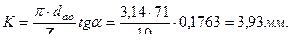
по ГОСТ 9324-80(см. табл. 3.1.4) принимаем К = 3 мм.
Поскольку фреза имеет класс С, ее зубья могут быть не шлифованными, поэтому значение К1 не определяем.
Осевой шаг фрезы
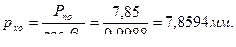
ПРИЛОЖЕНИЯ
Приложение 3.1
Приложение 3.2
Продолжение приложения 3.2
| Наименование проверяемых параметров | Обозначение | Класс точности | Для модулей (мм) | |||
| от 1 до 2 | св. 2 до 3,5 | св. 3,5 до 6 | ||||
| допуски и предельные отклонения, мкм | ||||||
| 4. Радиальное биение по вершинам зубьев
| frda | AA | 12 | 16 | 20 | |
| A | 20 | 25 | 32 | |||
| B | 32 | 40 | 50 | |||
| C | 50 | 63 | 80 | |||
| Д | 80 | 100 | 125 | |||
| 5. Профиль передней поверхности
Прямолинейность и наклон линии пересечения передней поверхности и плоскости, перпенди-кулярной оси фрезы на рабочей высоте зуба
|
| АА | 12 | 16 | 20 | |
| А | 20 | 25 | 32 | |||
| В | 32 | 40 | 50 | |||
| С | 63 | 80 | 100 | |||
| Д | 100 | 160 | 200 | |||
Приложение 3.3
Приложение 3.4
ЛИТЕРАТУРА
1. Грановский Г.И., Панченко К.П. Фасонные резцы. М.: Машиностроение, 1975. 309 с.
2. Иноземцев Г.Г. Проектирование металлорежущих инструментов: Учебн.пособие для вузов по специальности "Технология маиностроения, металлорежущие станки и инструменты". - М.: Машиностроение, 1984. - 272 с.
3. Маргулис Д.К. Протяжки переменного резания. М.:, 1962. 269 с.
4. Семенченко И.И., Матюшин В.М., Сахаров Г.Н. Проектирование металлорежущих инструментов. М.: Машгиз, 1962. 952 с.
[1] Грановский Г.И., Панченко К.П. Фасонные резцы. М.: Машиностроение, 1975. 309 с.
[2] Маргулис Д.К. Протяжки переменного резания. М.:, 1962. 269 с.
[3] Семенченко И.И., Матюшин В.М., Сахаров Г.Н. Проектирование металлорежущих инструментов. М.: Машгиз, 1962. 952 с.
Институт Металлургии, Машиностроения и Транспорта
Кафедра «Автоматы»
к.т.н., доц. Братчиков А.Я. ст. преподаватель Никитин А.В.
КУРСАВОЕ ПРОЕКТИРОВАНИЕ
Проектирование инструмента
С. Петербург 2016г.
ОГЛАВЛЕНИЕ
I. ФАСОННЫЕ РЕЗЦЫ... 5
1.ПРОЕКТИРОВАНИЕ ФАСОННОГО ДИСКОВОГО РЕЗЦА.. 19
1.1 МЕТОДИКА РАСЧЕТА ДИСКОВОГО ФАСОННОГО РЕЗЦА.. 19
1.1.1. Исходные данные: 19
1.1.2. Выбор базовой точки на профиле детали. 19
1.1.3. Выбор количества узловых точек N на профиле детали. 19
1.1.4. Выбор инструментального материала. 19
1.1.5. Выбор основных параметров дискового фасонного резца. 19
1.1.6. Выбор геометрических параметров режущей части резца. 21
1.1.7. Определение высоты установки резца относительно линии центров станка 22
1.1.8. Определение расстояния от оси резца до плоскости передней поверхности 22
1.1.9. Определение длины резца (см. рис.1.1.4) 22
1.1.10. Определение размеров стружечной канавки. 22
1.1.11. Коррекционный расчет профиля резца. 22
1.1.12. Назначение допусков и технические условия. 23
1.2. ЧИСЛОВОЙ ПРИМЕР РАСЧЕТА ДИСКОВОГО ФАСОННОГО РЕЗЦА 24
1.2.1. Исходные данные. 24
1.2.2. Выбор базовой точки на профиле детали. 24
1.2.3. Выбор количества узловых точек N на профиле детали. 24
1.2.4. Выбор инструментального материала. 24
1.2.5. Выбор основных конструктивных параметров дискового фасонного резца 25
1.2.6. Выбор геометрических параметров режущей части резца. 25
1.2.7. Высота установки резца относительно линии центров. 25
1.2.8. Расстояние от оси резца до плоскости передней поверхности. 25
1.2.9. Определение длины резца. 25
1.2.10. Выбор глубины заточки. 25
1.2.11. Коррекционный расчет профиля резца. 26
II. ПРОТЯЖКИ.. 27
ПРОЧНОСТЬ ПРОТЯЖЕК.. 45
2. МЕТОДИКА РАСЧЕТА КРУГЛОЙ ПРОТЯЖКИ.. 47
2.1. Исходные данные. 47
2.3. Определение подачи на зуб у режущих зубьев протяжки. 48
2.4. Суммарный подъем на зачищающие (чистовые) зубья. 49
2.5. Расчетная глубина впадины зубьев протяжки. 49
2.6. Расчетный шаг режущих зубьев. 50
2.7. Форма и размеры стружечной канавки в осевом сечении. 50
2.8.Определение геометрических параметров зубьев протяжки. 54
2.9. Максимальное число одновременно работающих зубьев протяжки 55
2.10. Наибольшее усилие протягивания. 55
2.11.Определение размеров хвостовика. 57
2.12. Диаметр передней направляющей части протяжки. 57
2.13. Проверка протяжки на прочность. 58
2.14.Определение размеров калибрующих зубьев протяжки. 61
2.15. Профиль и число калибрующих зубьев. 63
2.16. Число режущих зубьев. 64
2.17. Число и размеры стружкоразделительных канавок для режущих зубьев. 64
2.18. Определение общей длины протяжки (см.рис.2.1.4) 65
2.19. Определение допустимого радиального биения на режущих зубьях протяжки. 67
2.2. Числовой пример расчета круглой протяжки. 67
2.2.1. Исходные данные. 67
2.2.2. Определение припуска под протягивание. 67
2.2.3. Диаметр сверла D св для отверстий. 68
2.2.4. Определение подачи Sz на зуб у режущих зубьев протяжки. 68
2.2.5. Назначение суммарного подъема 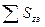 на зачищающие (чистовые) зубья протяжки. 68
на зачищающие (чистовые) зубья протяжки. 68
2.2.6. Расчетная глубина hp впадины зуба протяжки. 68
2.2.7. Расчетный шаг Pp режущих зубьев. 68
2.2.9. Определение геометрических параметров зубьев протяжки. 68
2.2.10. Максимальное число одновременно работающих зубьев протяжки 69
2.2.11. Наибольшее усилие протягивания составит (см. табл.2.1.7...2.1.9) 69
2.2.12. Размеры хвостовика назначаем по табл. 2.1.10. 69
2.2.13. Диаметр передней направляющей равен. 69
2.2.14. Проверка протяжки на прочность. 69
2.2.15. Определение размеров калибрующих зубьев потяжки. 70
2.2.16. Профиль и число калибрующих зубьев. 70
2.2.17. Число режущих зубьев. 71
2.2.18. Число и размеры стружкоразделительных канавок. 71
2.2.19. Общая длина протяжки L П (рис.2.1.4) 71
2.2.20. Допустимое радиальной биение на режущих зубьях протяжки. 72
III. ЧЕРВЯЧНЫЕ ФРЕЗЫ... 73
3. Зуборезные червячные фрезы... 75
3.1. МЕТОДИКА РАСЧЕТА ЧЕРВЯЧНОЙ ФРЕЗЫ... 84
3.1.1. Исходные данные. 84
3.1.2. Определение параметров исходной инструментальной рейки показано на рис.3.1.1 (см.табл.3.1.1). 84
3.1.3. Расчетный профильный угол 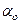 , инструментальной рейки в нормальном сечении (профильный угол фрезы) 84
, инструментальной рейки в нормальном сечении (профильный угол фрезы) 84
3.1.4. При нарезании прямозубого колеса (β=0) нормальный модуль mn . фрезы принимается равным модулю m 0 колеса. 85
3.1.5. Шаг по нормали Р no, между соседними профилями фрезы (рис.1) 85
3.1.6. Расчетная толщина зуба Sno фрезы по нормали к делительной окружности 85
3.1.7. Высота головки и ножки фрезы определяется по формуле. 85
3.1.8. Определение высоты hu . зуба фрезы. 85
1.9. Выбор типа и основных размеров фрезы (ГОСТ 9324-80). 85
3.1.10. Определение угла Ψ контакта фрезы.. 87
3.1.11. Число зубьев фрезы определяется по формуле: 87
3.1.12. Выбор геометрических параметров зуба фрезы. 87
3.1.14. Диаметр начальной окружности (табл.4) 90
3.1.15. Угол подъема витков фрезы на начальной окружности. 90
3.1.16. Осевой шаг фрезы.. 90
3.1.17. Определение угла установки фрезы на станке. 90
3.1.19. Наименьшая длина нарезанной части фрезы определяется по формуле 90
3.1.20. Расчетные размеры зубьев фрезы в нормальном сечении. 91
3.2. Числовой пример расчета червячной фрезы.. 91
3.2.1. Исходные данные. 91
3.2.2. Параметры зубьев колеса (зубчатой рейки) 91
3.2.3. Расчетный профильный угол 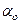 инструментальной рейки в нормальном сечении (профильный угол фрезы) для эвольвентного зацепления
инструментальной рейки в нормальном сечении (профильный угол фрезы) для эвольвентного зацепления  .................. 91
.................. 91
3.2.4. Нормальный модуль фрезы принимаем равным модулю колеса (прямозубое колесо) 91
3.2.5. Шаг по нормали Pno между соседними профилями фрезы (см. рис.3.1.1) 91
3.2.6. Расчетная толщина зуба Sno по нормами к делительной окружности 91
3.2.7. Высота головки и ножки зуба. 91
3.2.8. Высота зуба фрезы.. 91
3.2.9. Выбор типа фрезы.. 92
3.2.10.Угол контакта фрезы.. 92
3.2.11. Число зубьев фрезы.. 92
3.2.12. Геометрические параметры зубьев фрезы принимаем 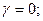 ........ 92
........ 92
3.2.13. Падение затылка. 92
3.2.14.Диаметр начальной окружности фрезы.. 92
3.2.15 Угол подъема витков фрезы на начальной окружности. 92
3.2.16. Осевой шаг фрезы.. 93
3.2.17. Угол остановки фрезы на станке. 93
3.2.18.Глубина стружечной канавки (для нешлифованного зуба) 93
3.2.19 Наименьшая длина на нарезанной части фрезы.. 93
3.2.20. Уточнение размеров зубьев фрезы в нормальном сечении. 93
ПРИЛОЖЕНИЯ.. 94
Приложение 3.1
Параметры шероховатости и точности обработки поверхностей червячных зуборезных фрез. 94
Приложение 3.2
Контроль точности изготовления фрез. 95
Приложение 3.3
Размеры профиля зубьев фрез в осевом сечении. 97
Приложение 3.4
Размер шпоночных пазов в инструменте, мм.. 98
ЛИТЕРАТУРА.. 99
I. ФАСОННЫЕ РЕЗЦЫ
Фасонные резцы широко применяют в массовом и крупносерий-
ном производстве для обработки сложного профиля деталей тел
вращения или призматических деталей. На деталях тел вращения
обрабатывают как наружные, так и внутренние поверхности на
токарных, револьверных станках, полуавтоматах и автоматах. Фа-
сонные поверхности на призматических деталях изготовляют фасон-
ными резцами на фрезерных и строгальных станках.
Фасонные резцы имеют ряд преимуществ по сравнению с обыч-
ными токарными резцами. Они обеспечивают:
1)высокую производительность вследствие значительного умень-
шения машинного и вспомогательного времени за счет сокращения
пути резания при радиальной подаче и времени на установку и
наладку резца;
2) высокую точность формы и размеров обрабатываемых деталей,
а также их идентичность и взаимозаменяемость;
3) простоту эксплуатации, так как их перетачивают только
по передней поверхности.
Однако стоимость фасонных резцов выше, чем простых токарных
резцов. Несмотря на это, в массовом и крупносерийном производстве
они вполне рентабельны. Фасонные резцы подразделяют по форме
на круглые и призматические (рис, 1.1.а, б); по виду обрабатывае-
мой поверхности – на наружные и внутренние (рис. 1.1.а, г); по
установке и направлению подачи относительно обрабатываемой
детали – на радиальные и тангенциальные (рис. 1.1.б, в); по форме
образующих фасонных поверхностей — на кольцевые и винтовые
(рис. 2.1.е, ж, и); по расположению резца относительно детали – с параллельным расположением осей или баз или с повернутым
(рис. 2.1.е, ж) и по расположению передней поверхности – без
наклона и с наклоном под углом л (рис. 1.1.а, д). Призматические
резцы изготовляют только для обработки наружных поверхностей.
Круглые резцы, как правило, работают с радиальной подачей и их применяют для обработки как наружных, так н внутренних поверх-
ностей. При этом для последних применяют кольцевые и винтовые
резцы.

Рис. 1.1. Типы фасонных резцов
Причины искажения профиля фасонного резца. Профиль фасонного резца определяется в сечении, нормальном к его задней поверхности. В этом сечении рассчитывают и задают размеры профиля и
осуществляют его контроль. Однако формообразующей поверхностью детали является режущая кромка. Профиль резца в нормальном сечении не совпадает с линией режущей кромки. В свою очередь, линия режущей кромки резца может отличаться от профиля обработанной детали в ее осевом сечении. Следовательно, профиль фасонного резца отличается от профиля обработанной детали. Причиной этого несоответствия является наличие у резца переднего и заднего углов. Для уяснения этого вопроса рассмотрим рис. 1.2.
Возьмем один участок детали в виде усеченного конуса. В первом случае (рис.1.2, а), когда передний н задний углы резца равны
нулю, высота профиля резца B1 равна разности радиусов обработанной детали, т. е. В1 = r2 - r1. Профиль резца соответствует режущей кромке и профилю детали. Но это нереальный случаи, т.е. резец не может иметь нулевой задний угол. Заметим, что для неповернутых резцов их размеры в осевом направлении детали не изменяются.
Во втором случае (рис. 1.2, б) у резца передний угол γ1>О,
а задний угол α1 = 0. При этом высота профиля резца В2<( r2 - r1),
т. е. меньше В1. Отсюда следует, что если угол γ≠0, то профиль
резца будет отличаться от профиля режущей кромки, а значит и от профиля обрабатываемой детали.

Рис. 1.2. Влияние γ и α на высоту профиля резания
В третьем случае (рис. 1.2, в) угол γ = 0, а угол α > 0. Здесь также высота профиля резца меньше высоты профиля детали, т. е. В3<( r3 — r1); В= B1· cosα1.Следовательно, задний угол также создает отклонение профиля резца от профиля детали. Наконец, последний случай (рис. 1.2, г) соответствует реальным условиям, когда у резца α>0 и γ>0. В этом
случае B4<В3 и В4<В2. Таким образом, совместное влияние перед-
него у и заднего а углов увеличивает отклонение профиля резца
от режущей кромки и от профиля детали.
Будем считать передние и задние углы основными причинами,
которые вызывают указанное отклонение. Это отклонение не создаст
погрешность, оно является необходимым, преднамеренным. Вследствие этого профиль фасонного резца должен быть определен расчетным путем. Только при таком определенном отличии профиля резца
от профиля детали, которое устанавливается расчетным путем, за-
данная деталь будет обработана точно.
Профилирование фасонных резцов. Существуют графический
и аналитический методы определения профиля фасонных резцов.
Графический метод наглядный, но неточный, поэтому в инженерной
практике не применяется. Аналитический метод лишен этого не-
достатка, но более сложный. Несмотря на это, высокие требования
к точности проектирования фасонных резцов обусловили применение на практике аналитического метода. Существует несколько способов расчета профиля фасонных резцов. Рассмотрим общий способ точного аналитического решения задачи профилирования резцов, а также один из способов, основанный на решении трехчленных уравнений, который является также точным, но простым и наглядным.
Таблица 1.1.
Значения переднего угла для фасонных резцов
Обрабатываемый
Материал
Сталь σв, МПа
Чугун, НВ
Латунь
Бронза
Свинцови-
Стая
Красная
Медь, алюминий
Решение задачи сводится к тому, чтобы определить необходимый
профиль резца в нормальном сечении к его задней поверхности,
при котором режущие кромки резца могли бы правильно обработать
заданную деталь. Исходными параметрами для расчета являются
размеры обрабатываемой детали, заданные чертежом, и свойства
обрабатываемого материала. Вначале задаются значением переднего
и заднего углов резцов. Для фасонных резцов из быстрорежущей
стали, работающих с радиальной подачей, оптимальный задний
угол α = 10...150. Для резцов из твердого сплава α = 8...120. Передний угол у в зависимости от свойств обрабатываемого материала для
резцов из быстрорежущей стали рекомендуется принимать по
табл. 1.1. Для резцов из твердого сплава передний угол принимают
на 5...100 меньше.
Фасонные резцы можно устанавливать по высоте центров обрабатываемой детали (по центру) одной вершинной точкой или же
линией – режущей кромкой. В последнем случае это может быть
только для цилиндрического или конического участка детали. Для
поверхностей криволинейного профиля или торцовых этого достигнуть невозможно. На практике чаще применяются резцы первого
вида, устанавливаемые по центровой линии детали одной точкой,
расположенной в вершине режущей кромки. Для обработки наружных поверхностей тел вращения эта точка контакта находится
на наименьшем диаметре обрабатываемой детали; для обработки
внутренних поверхностей – на наибольшем диаметре отверстия.
Общий аналитический способ профилирования резцов. Для определения профиля фасонного резца общим аналитическим способом
необходимо найти режущую кромку как линию пересечения поверх-
ности детали с плоскостью передней грани резца, принять ее за об-
разующую поверхности резца и определить линию сечения резца
плоскостью, нормальной к задней поверхности инструмента. Для
этого необходимо решить следующие задачи.

Рис. 1.3. К определению уравнения конической поверхности детали
1.Записать уравнение поверхности заданной детали в системе XYZ (рис.1.3). Для участка детали в виде усеченного конуса параметрическое уравнение такой поверхности имеет вид:
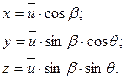 1.1
1.1
Здесь параметры ū и θ изменяются в диапазонах 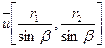 ;
; 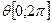 , где r1 и r2 – наименьший и наибольший радиусы детали; β – угол наклона образующей конуса.
, где r1 и r2 – наименьший и наибольший радиусы детали; β – угол наклона образующей конуса.
Если учесть, что из первого уравнения системы (1.1) 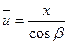 ,
,
то эту систему уравнения можно записать
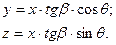 1.2
1.2
В уравнениях (1.2) абсциссой х задаются.
2. Уравнение плоскости 1 – 2 передней поверхности резца в си-
стеме координат XYZ имеет вид (рис. 1.4)
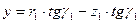 1.3
1.3
где γ1 – передний угол резца в расчетной точке 1.
3. Решив совместно уравнения (1.2) и (1.3), получим уравнения
линии режущей кромки резца в системе координат детали XYZ
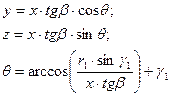 1.4
1.4

Рис. 1.4. Схема для аналитического профилирования фасонного резца: а – призматического; б – круглого
4. Преобразуем систему координат XYZ в систему Xр Yр Zр,
связанную с резцом. Для призматического резца (рис. 1.4, а) эта связь координат точек режущей кромки определяется матричным;
равенством
 1.5
1.5
где М – матрица перехода из системы XYZ в систему XPYPZр.
В соответствии с рис. 1.4, а матрица
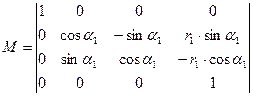 1.6
1.6
Тогда формулы перехода из системы XYZ в систему XPYPZр.
примут вид
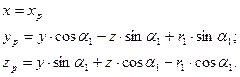 1.7
1.7
где α1 – задний угол резца в точке 1.
5. Подставив в уравнения (1.7) формулы для координат y, z
из уравнений (1.4), получим координаты точек, т. е. уравнения ре-
жущей кромки призматического резца в системе ХРУ p Zp
 1.8
1.8
Введем неподвижную систему координат X' P Y' P Z' P, совпадающую
вначале с системой XPYр Zр, которую принимаем за подвижную.
Для образования задней поверхности резца сообщим подвижной системе координат, а вместе с ней и режущей кромке движение вдоль
оси Y' P. Тогда уравнение этой поверхности запишется
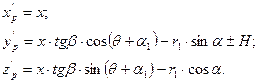 1.9
1.9
где Н – текущее значение параметра, формообразующего заднюю
поверхность.
Плоскость, нормальная к задней поверхности резца, есть координатная плоскость X' P Y' P или любая другая, параллельная ей, уравнение которой y' P = 0 или y' P = ± Н.
6. Если принять y' P = 0, то искомый профиль призматического фасонного резца в сечении нормальной плоскостью запишется
уравнением
 1.10
1.10
Анализ уравнения (1.10) показывает, что профиль резца получается криволинейным (вогнутым). Если режущую кромку совместить с образующей конуса так, чтобы λ = 0, то она будет прямолинейной. В этом случае профиль призматического резца будет тоже
прямолинейным. Для образования круглого резца найденной режущей кромке необходимо сообщить круговое движение относительно
оси резца Хр. Задача по отысканию профиля круглого фасонного
резца в нормальном (осевом или радиальном) сечении сводится
к определению расстояний точек режущей кромки, описываемой
уравнением (1.4), до оси круглого резца.
Положение оси резца задается координатами ур и rр (рис. 1.4, б),
которые определяются через исходные постоянные величины r1,
R1 и α1,:
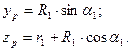 1.11
1.11
Ось круглого резца в системе XyYpZp проще задать единичным
вектором ī с направляющими коэффициентами
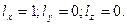 1.12
1.12
который проходит через точку центра резца с координатами хр, yр, zР.
Расстояние R от точки режущей кромки с координатами х, у, z
до прямой ī (lx, ly, lz), заданной единичным вектором (1.12) и про-
ходящей через ось Хр резца, определяется по формуле
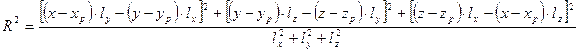 1.13
1.13
Подставив в формулу (1.13) значения x, y и z из уравнения (1.4)
и учитывая коэффициенты lx, ly, lz и координаты точки Ор (О, ур, zp),
получим уравнение для определения искомого радиуса резца
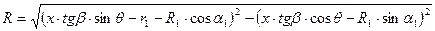 1.14
1.14
где угол θ находится из совместного решения уравнении (1.2) и (1.3):
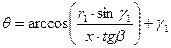 1.15
1.15
Зная разность радиусов R1– R резца и его осевые размеры,
находим профиль инструмента. Высота профиля В= R1– R. Для
точного определения профиля резца в уравнении (1.14) необходимо задаться рядом значений текущих осевых размеров х детали и для
каждого из них найти радиус R. Обычные вычисления окажутся
слишком трудоемкими, поэтому данную задачу целесообразно решать на ЭВМ, используя формальные языки программирования.
Преобразуем третье уравнение системы (1.10) к виду, позволяющему находить угол θ как функцию его тангенса:
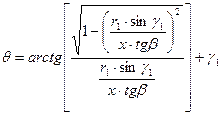 1.16
1.16
Введем в формулу (1.16) обозначения: S1 = r1 · sinγ, S2 = x· tg β; S3 = S1/ S2, после чего выражения (1.14) и (1.16) примут
вид
 1.17
1.17
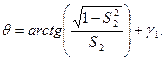 1.18
1.18
При заданном числе точек n на оси X от xmin до х max определим
шаг Δ x изменения координаты х:
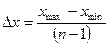 1.19
1.19
Определение профиля фасонных резцов геометрическим способом.
Как уже отмечалось, этот способ основан на решении простых трех-
членных уравнений, широко используемых на практике. Пусть
размеры обрабатываемой детали заданы в соответствии с рис. 1.5.
С учетом качества обрабатываемого материала по табл. 1.1 выбираем
передний угол γ1. Задний угол α1 принимаем равным 10...120. Для
примера рассмотрим методику профилирования круглого фасонного
резца. Расчет профиля резца для обработки различных участков
детали ведут последовательно от одной базовой точки 1 или ли-
пни 1—1, в которой для неповернутых резцов его вершину устанавливают по высоте центров детали. Расчетная схема строится без
масштаба. Для конического участка детали 1—2 она показана на
рис. 1.6. Прежде всего определим исходный наружный диаметр Dl
резца или радиус R1. Для этого рассчитаем диаметр оправки d
из условия ее работы на сложное сопротивление. Исходный наружный диаметр резца D1≈(2,5...3)· d. Диаметр оправки принимают
из соотношения d≈0,4· l, где l – длина обрабатываемой детали.
Расчетные диаметры резца и оправки принимаются по приведенному
ниже нормальному ряду.
| d, мм | 12 | 16 | 20 | 22 | 24 | 28...30 | 32...36 |
| D, мм | 30...40 | 40...50 | 50...60 | 60...70 | 70...80 | 80...90 | 90...100 |
Центр круглого резца выше центра обрабатываемой детали на
величину h. Это необходимо, чтобы образовать задний угол α резца:
h = R1· sinα1, где α1 – задний угол резца в точке 1.

|
|
Методика определения профиля резца следующая. Сначала решают систему прямоугольных треугольников, связанных с обрабатываемой деталью, из которых находят
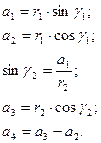
где γ2 – передний угол резца в точке 2 его контакта с деталью.
Затем решают систему двух прямоугольных треугольников, связанных с резцом, из которых
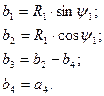
где ψ1 – уол искажения в точке 1, ψ1 = γ1 + α1, ψ2 – угол искажения в точке 2, ψ2= γ2+α2; tgψ2= 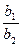 ; α2 – задний угол резца в точке 2. Тогда искомый радиус резца
; α2 – задний угол резца в точке 2. Тогда искомый радиус резца
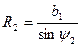 1.20
1.20
а высота профиля резца В1 = R1 – R2
Для условных (нереальных) участков 1–3 и 1–4 детали (см.
рис. 1.5) профиль резца рассчитывают таким же способом.
Определение профиля фасонного резца от одной
базовой точки 1 имеет то преимущество, что при построении расчетных схем для условных участков детали 1–3 1–4 и т.д. малый
треугольник Oa1, связанный с деталью, и большой прямоугольный
треугольник ОРВ1, связанный с резцом, остаются неизменными
(см. рис. 1.6). Поэтому их размеры определяются только один раз
по первой расчетной схеме. Вследствие этого сокращаются вычисления. Кроме того, найденные размеры профиля резца определяются
от этой базовой точки 1 или линии 1–1. Во всех случаях высота
профиля резца получается меньше высоты профиля обрабатываемой
детали. Анализ приведенных уравнений показывает, что профиль
фасонных резцов зависит от параметров обрабатываемой детали и
инструмента. Наибольшее влияние на профиль резца оказывает
угол конуса детали β, затем передний и задний углы и в меньшей
мере размеры резца.
Профиль резца по крайним точкам можно рассчитать только для
участков детали, имеющих торцовые уступы. Резцы, рассчитанные
таким способом для конических поверхностей, имеют погрешности
при обработке. Если передний угол положительный и режущая
кромка принимается прямолинейной, то она не будет совпадать с образующей конуса (рис. 1.7), а является наклонной к ней под углом λ.
Так как режущая кромка является формообразующей, то обработанная поверхность детали будет не конической, а вогнутой в виде
гиперболоида вращения. В результате возникнет погрешность Δ1
которую можно устранить, совместив режущую кромку с образующей конуса путем поворота резца на угол К или заточкой его перед-
ней поверхности под этим углом. Но так можно делать только для
деталей, состоящих из одного конического участка. Для сложного контура деталей, имеющих несколько участков, этого сделать нельзя. В более общем случае такая погрешность будет устранена, если для расчета профиля резца взять несколько точек (сечений) на конической поверхности детали. Тогда режущая кромка и профиль резца будут криволинейными – вогнутыми.

Рис. 1.7. Образование погрешностей детали круглым фасонным резцом.
Однако резцы с криволинейным профилем нетехнологичны. В ряде случаев сложная поверхность круглого резца заменяется более простой – конической. В этом случае режущая кромка резца будет выпуклой, так как она лежит в передней плоскости, которая не проходит через ось резца,
а отстоит от нее на расстоянии Н. В результате возникнет погрешность обработки детали, равная Δ2 (рис. 1.7). Суммарная погрешность обработки резцом конической формы Δ = Δ1 + Δ2. Выпуклость режущей кромки аналитически определена в работе [4].
На рис. 1.8 показана схема для решения этой задачи. Находим
наибольшее отклонение Δ y. Режущая кромка с наибольшей выпуклостью лежит в плоскости передней поверхности резца. Отклонение
Δ y есть проекция Δ2 на осевую плоскость резца, определяемое
в направлении, перпендикулярном его оси. Запишем уравнение
конической поверхности резца
 1.21
1.21

Рис. 1.8. Определение выпуклости режущей кромки резца
где b = х· tgβ; ρ – текущий радиус-вектор на конической поверхности резца; R1 — радиус резца в точке 1; β – угол наклона образующей конической поверхности резца.
Уравнение передней плоскости у=а+а1 где а=а2+а3;
а2 = R1· cos α1; a3 = R1· sin α1/ tg γ; а1 = z· ctgγ1
Таким образом, у = a – z· ctg γ1 или
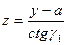 1.22
1.22
Решив совместно уравнения (1.21) и (1.22), получим квадратное
уравнение, которое описывает гиперболическую режущую кромку
резца 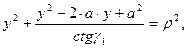 откуда
откуда
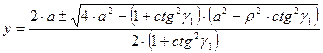 1.23
1.23
Из рис. 2.8 видно, что
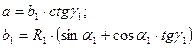 1.24
1.24
Подставим значение а в уравнение (1.23) и после некоторого преобразования получим окончательное уравнение режущей кромки I
резца
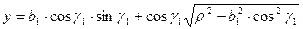 1.25
1.25
где γ1 – передний угол резца в точке 1.
Уравнение прямой линии, проходящей через крайние точки 1–2
(см. рис. 1.8) режущей кромки,
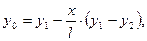 1.26
1.26
где y1 и y2 – ординаты точек 1 и 2. Из уравнения (2.21) имеем
 1.27
1.27
Подставив уравнение (1.27) в уравнение (1.26), получим
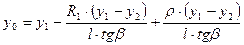 1.28
1.28
Величина стрелы выпуклости режущей кромки Δ y = у – у0 т. е.
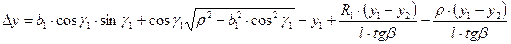 1.29
1.29
Максимальная выпуклость получится при значении ρ, для которого первая производная  .
.
Дифференцируя уравнение (1.29) и подставив значение b1, из (1.24) получим
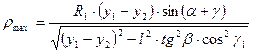 1.30
1.30
+

Рис. 1.9. Призматический (а) и круглый (б) фасонные резцы
Подсчитав по уравнению (1.30) ρmax и подставив его в уравнение (1.29), получим максимальную выпуклость режущей кромки
круглого конического резца, который установлен только одной
вершинной точкой на высоте центра изделия. Подставив значение ρmax в уравнение (1.27), получим значение абсциссы х, определяющей точку режущей кромки, к которой относится максимальная выпуклость. Исследования, приведенные в работе[1], показали, что наиболее точными являются призматические резцы, у которых прямолинейная режущая кромка совпадает с образующей конуса обрабатываемой детали. В этом случае не возникает погрешность обработки. Это справедливо и для призматических тангенциальных резцов.
Призматические резцы, устанавливаемые только одной точкой
режущей кромки по центру обрабатываемой детали, создают незначительную погрешность. Наибольшая погрешность возникает при
работе круглыми коническими резцами. Для конических резцов
95 % общей погрешности составляет выпуклость режущей кромки.
Детали, обработанные такими резцами, могут иметь вогнутость
0,5...1,5 мм. Задача по определению профиля призматических резцов решается более просто, чем для круглых. Для участка 1–2
высота профиля призматического резца В1= a4· cosψ1 (см. рис. 1.6).
Для радиусных участков деталей фасонные резцы профилируют по
приведенной выше методике. Задаются несколькими точками на
радиусном участке детали и находятся также координаты соответствующих точек профиля резца. Расчетный профиль резца получается криволинейным. Для несопряженных радиусных участков с невысокой точностью криволинейный профиль резца заменяют соответствующим радиусом.
Дата: 2019-07-30, просмотров: 410.