Общий случай расчета п.п. классическим методом.

Задается положительное направление тока (произвольно)

1) Определяем принужденное значение токов и напряжения до коммутации (ТОЭ, ч.1)

2) Составляем систему уравнений по законам Кирхгофа для свободных токов и напряжений, где

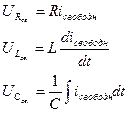
3) Производим алгебраизацию системы диф. уравнений, т.е. заменяем , .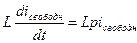

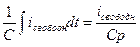4) Находим определитель системы и приравниваем его к 0, т.е.

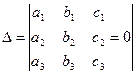
5) Отсюда, определяем корни характеристического уравнения р₁, р₂, р₃, …,р_n.

Примечание.

Если в электрической цепи отсутствует индуктивно связанные элементы, то характеристическое уравнение можно получить, не составляя диф. уравнения, пользуясь выражением для входного сопротивления одной из ветвей, заданной после коммутационной цепи на переменном токе. Z _вх(jw) заменив в нем jw на р (оператор р) и уже Z _вх (р)=0.

/**

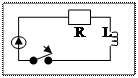после переходного процесса

Z _вх(jw)=R+jwL

Z _вх(р)= R+pL=0

p=R/L (c^-1)

**/

6) С учетом полученных корней записываем выражение для искомого тока (напряжения)

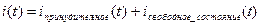
Если характеристическое уравнение 1-го порядка, то выражение для свободного тока содержит одну постоянную интегрирования.

i_св. = А*е^р1t – это значит всего один накопитель в цепи.

Если характеристическое уравнение 2-го порядка, то выражение для свободного тока содержит две постоянных интегрирования.

i_св. = А₁*е^р1t + А₂*е^р2t .

Количество индуктивности и емкости в целом соответствует количеству А.

Если корни характеристического уравнения действительные и разные, то

i_св.=А₁*е^р1t+А₂*е^р2t+..+ А_к*е^ркt.

Если корни действительные и равные, то (р=р₁=р₂=..=р_м), то

i_св.=А₁*е^рt+А₂*t*е^рt+А₃*t³*е^рt+..+ А_к*t^m-1*е^рt.

Если корни пара комплексно сопряженных корней, то

p_1,2=-a 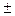jw₀,

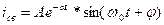, где постоянными интегрирования являются А,j.

7) На основании 1-ого и 2-ого законов коммутации определяем независимые начальные условия, т.е.       i_L (0-) = i_L (0)

u_c(0-)= u_c(0)

8) Определяем зависимые начальные условия, необходимые для нахождения постоянных интегрирования.

Определение зависимых начальных условий производится на основе независимых начальных условий и законов Кирхгофа.

При составлении уравнений по 2-му закону Кирхгофа следует выбирать контуры так, чтобы они содержали минимум накопителей энергии.

В уравнении 1-ого порядка для определения единственной постоянной интегрирования достаточно найти начальное значение искомого тока (напряжения).

В уравнении 2-ого порядка для определения 2-х постоянных интегрирования требуется найти начальное значение исходной функции и ее 1-ой производной.

И т.д.

9) Определяем постоянные интегрирования

а) при одной постоянной интегрирования

i_св. = А*е^рt

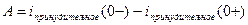
ток при t=0 не может измениться скачком.

б) при 2-х постоянных интегрирования. Для их определения необходимо иметь два уравнения .Второе получаем путем дифференцирования 1-ого по времени.

- если корни характеристического уравнения 2-ого и выше порядка действительны и неравны

i_св.=А₁*е^р1t+А₂*е^р2t.

i^/_св=А₁*р₁+А₂*р₂*е^р2t.

При t=0      i_св(0)=А₁+А₂. - независимые начальные условия

i^/_св(0)=А₁*р₁+А₂*р₂. - зависимые начальные условия

Отсюда следует А₁, А₂.

- если корни характеристического уравнения являются комплексно-сопряженными числами, то

,

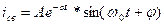p_1,2=-a jw₀,

,

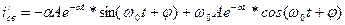При t=0 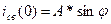        - независимые начальные условия

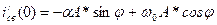- зависимые начальные условия

Отсюда следует А,j.

10) Записываем выражения искомых функций:

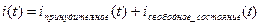
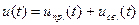
По окончанию решения проверить удовлетворяет ли оно начальным условиям, подставить в решение t=0.