Основные сведения об электрических цепях.

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Основные сведения об электрических цепях.

Электрическая цепь - идеализированная совокупность устройств, предназначенных для производства, передачи, распределения электрической энергии и преобразования ее в другие виды.

Основные элементы: источники и приемники электроэнергии.

Источники энергии носят названия активных элементов эл. цепи.

Часть эл. сетей, состоящая только из последовательно включенных источников ЭДС и R и ограниченно с обеих сторон узлами, называют ветвью.

Последовательные соединения - элементы цепи, обтикаемые одним и тем же током.

Электрическая схема - условное графическое изображение реальной эл. цепи.

Узлом эл. цепи - место соединения 3-х и более ветвей.

Различные ветви образуют контура (замкнутая цепь, образованная несколькими ветвями).

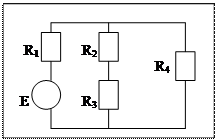Независимый контур - контур, в который входит хотя бы 1 ветвь, не вошедшая в предыдущие контура.

Здесь

два независимых

контура

Эквивалентные цепи источников энергии.

1. Источник ЭДС (напряжение) - идеализированный источник эл. энергии, внутреннее сопротивление которого равно нулю.

по ГОСТу (обозначение):

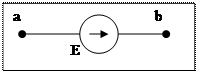
- положительное направление

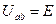
Реально:

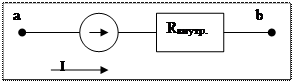
2. источник тока j - идеализированный источник эд. энергии, внутреннее сопротивление которого бесконечно велико.

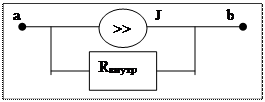
- положит. направление тока

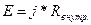
Законы Кирхгофа.

Пусть ЭДС и сопротивления нам известны.

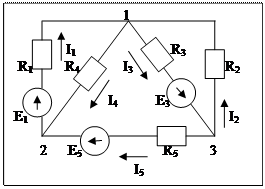Выберем произвольно положительное направление тока.

В данной схеме 3 узла, 5 ветвей.

Первый закон Кирхгофа. (применяется к узлам)

Алгебраическая сумма токов в узле равна нулю.

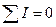
Токи, подтекающие к узлу берут со знаком «-», а оттекающие - «+».

----------------------------------

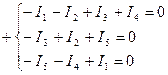
0=0

По 1-му закону Кирхгофу количество уравнений - ( n -1), где n - число узлов эл. схемы.

Второй закон Кирхгофа (применяется к контурам).

В любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях входящих в этот контур равна алгебраической сумме ЭДС.

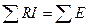
Обход тока по контуру выбирается положительным по часовой (с «+») и отрицательный против часовой стрелки (с «-»).

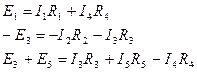
Количество уравнений по 2-му закону Кирхгофа всегда будет совпадать с количеством независимых контуров.

Недостаток метода расчета по з. Кирхгофа - неограниченное количество уравнений.

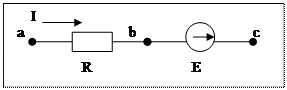
Обобщенный закон Ома.

Ток всегда течет от более высокого к более низкому потенциалу.

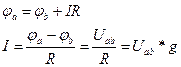- Закон Ома в потенциальной форме.

(g-проводимость)

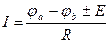- обобщенный закон Ома.

Преобразование электрических цепей

Преобразовать часть эл. схемы значит представить ее в другом виде, но таким образом, чтобы ток во всех ветвях и потенциалы всех узлов непреобразованной части эл. схемы остались без изменения.

Комплексная плоскость

Комплексная мощность

Среднее значение мощности за период:

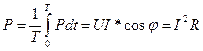- (Вт) - активная мощность (идет на выделения тепла в окружающую среду)

Ðj - разность фаз между напряжением и током

cos j - коэффициент мощности, важнейший энергетический показатель.

- (ВА) - полная (кажущаяся) мощность, т.е. та максимальная мощность, которую можно получить, если cos j =1 (i и u совпадают по фазе)

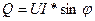- реактивная мощность ( теоретически: мощность, которой обмениваются генератор и нагрузка).

>0, если нагрузка носит индуктивный характер.

<0, если нагрузка носит емкостной характер

Ед. измерения реактивн. мощности «вар» (вольт ампер реактивное)

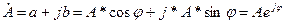
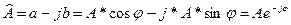-сопряженное к 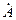число

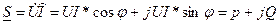
Топографическая диаграмма

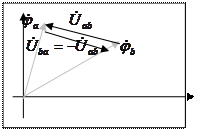
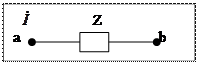
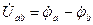
Первый индекс U напряжения (ab) указывает к какой точке направить стрелку вектора напряжения

Каждой точке на электрической схеме соответствует точка на комплексной плоскости.

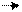
Топографическая диаграмма (ТД) - разновидность векторной диаграммы (ВД), при которой каждая точка на комплексной плоскости соответствует определенной точке электрической цепи. Координаты точки на комплексной плоскости равны соответственно действительной и мнимой частям потенциала данной точки электрической цепи, при этом, векторная диаграмма токов ВСЕГДА совмещается на одном чертеже с топографической диаграммой напряжения.

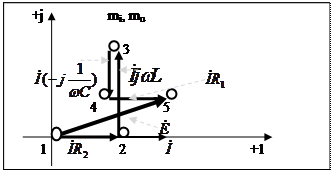
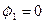
(индекс против тока)

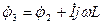
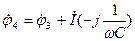
Комплексная форма записи

, ( )

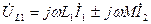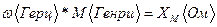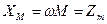- сопротивление взаимной индукции

Правило знаков: если положительное направление токов одинаково сориентированы относительно одноименных зажимов 2-х магнитосвязанных катушек, то на каждой катушке напряжение взаимной индукции пишется с тем же знаком, что и напряжение самоиндукции.

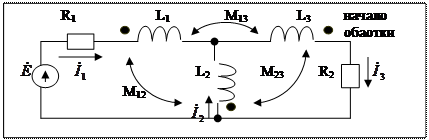Состав по 2-му закону Кирхгофа:

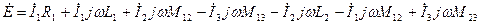
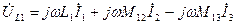
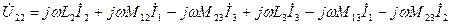
Параллельный резонанс

(резонанс тока)

/* */

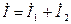
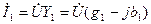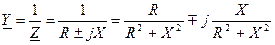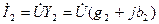
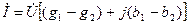
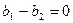-резонанс

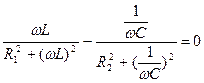-частный случай резонансов в параллельных ветвях

сопротивление емкости мы считаем идеальным R₂=0. Отсюда следует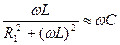

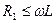
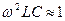
Классический метод

(заключающийся в интегрировании дифференциальных уравнений, связывающий токи и напряжения в переходном режиме. В результате этого появляются постоянные интегрирования, которые определяются из законов коммутации).

Ый закон коммутации

В любой ветви с индуктивностью ток и магнитный поток в момент коммутации (при t=0) сохраняет те же значения, которые они имели непосредственно перед коммутацией и далее начинают изменяться с этих значений.

Математ. запись:

i_L (0-) = i_L (0) , т.е. ток на индуктивности не может измениться скачком

Док-во:

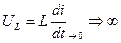Þ 2-ой закон Кирхгофа не соблюдается.

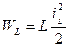-энергия магнитного поля.

Ой закон коммутации

В любой ветви напряжение и заряд на емкости сохраняет в момент коммутации (при t=0) те же значения, которые они имели непосредственно перед коммутацией и далее начинают изменяться с этих значений.

u_c(0-)= u_c(0) , т.е. напряжение на емкости не может измениться скачком

Док-во

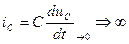
Переходный, принужденный (установившийся) и свободный

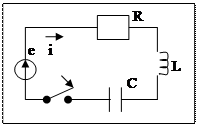процессы

Для любого момента времени в переходном режиме 2-ой закон Кирхгофа:

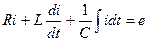(1)

где i – ток переходного режима

R*i_{принужденный (установившийся)}.

(2)

i-i_{принужд.} = i_{свободн.} (3)

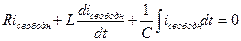(4)

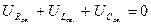
Это разложение токов и напряжений на свободные и принужденные соответствует лишь правилу решения линейных неоднородных дифференциальных уравнений, согласно которому общее решение таких уравнений равно сумме частного решений неоднородного уравнения и общего решения однородного уравнения.

i_св. – представляет собой общее решение однородного дифференциального уравнения (1) и записывается в виде показательной функции:

i_св. = А*е^р^t,

где А – постоянная интегрирования,

р –корень характеристического уравнения

i_прин – представляет собой частное решение неоднородного дифференциального уравнения (2). Определяется теми же методами, что и при законах Кирхгофа.

i= i_прин + i_св_. = i_прин + А*е^р^t – общее решение

(i= i_прин + А₁*е^р1^t+ А₂*е^р2^t – в зависимости от количества накопителей, в нашей схеме их два: L и C)