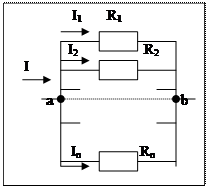
- сопротивление проводимости.

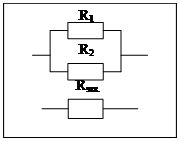Частный случай:

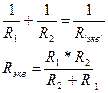
Пример: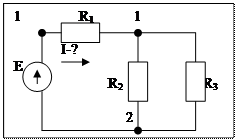

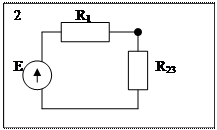
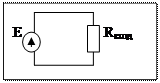
Следствие из схем 1 и 2

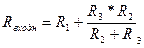
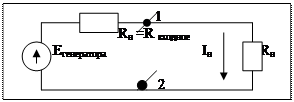Метод эквивалентного генератора

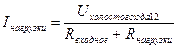
Электрические цепи однофазного синусоидально тока

Синусоидальный ток и основные величины, характеризующие его

Ток, изменяющийся во времени называется переменным и обозначается i(t)

Ток, для которого справедливо равенство i(t+T), называется периодическим, где T - постоянный промежуток времени (период переменного тока).

Значение переменной величины в какой либо момент времени называется ее мгновенным значением.

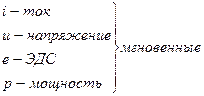
Синусоидальный (гармонический) ток -ток, мгновенное значение которого определяется равенством:

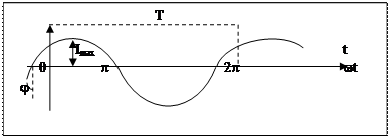
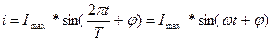
I_max  -амплитуда

T - период колебания, min интервал времени, когда функция повторяет все свои значения

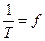 - частота (Герц) - число циклов повторения в 1 сек.

(Т=0,02сек. при f=50 Герц)

//** Добровольский изобрел трансформатор, генератор, линии эл. передач)**//

В радиотехнике применяются 3*10^-10 Герца

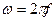- угловая частота, характеризующая скорость изменения функции.

,                   50 Герц- промышленная частота

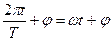 -фаза, характеризует состояние колебания, т. е. численное значение величины в данный момент времени.

При t=0 - фаза называется начальной.

Любая синусоидальная изменяющаяся функция определяется 3-мя величинами: амплитудой, угловой частотой и начальной фазой.

Действующее значение тока

Действующее значение переменного тока - такое эквивалентное значение постоянного тока, при котором постоянный ток, совершает ту же работу, что и переменный ток с заданной амплитудой за одно и то же время.

(А-работа= мощность*время)

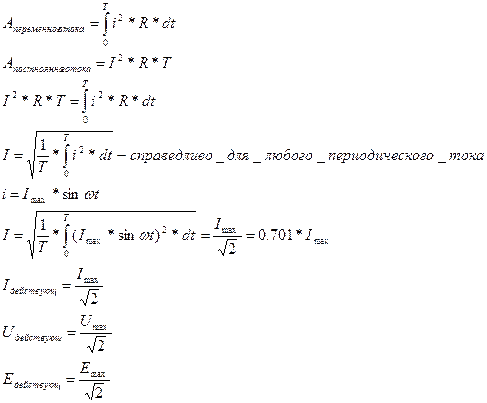
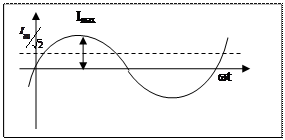Действующее значение переменного тока обладает при протекании через аналогичное активное сопротивление таким же тепловым воздействием, как и постоянный ток за один и тот же период.

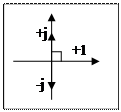
Комплексная плоскость

Изображение комплексных чисел в различных формах

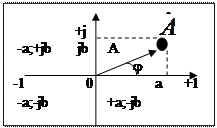
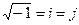 - комплексное число

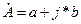 - комплексная величина, алгебраическая форма записи комплексного числа.

+j,-j - комплексная ось

+1,-1 - действительная ось

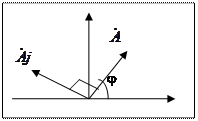
А - модуль комплексного числа

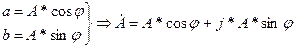 - тригонометрическая форма записи комплексного числа

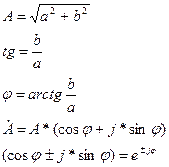е=2,712

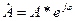 - показательная форма записи комплексного числа

Действия с комплексными числами

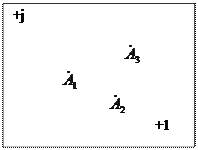
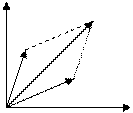Пусть даны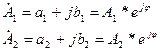

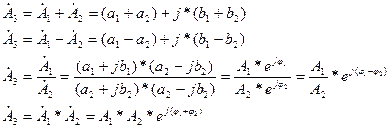
Сложение и вычитание производить в алгебраической форме записи

Деление и умножение желательно производить в показательной форме

Умножение вектора комплексного числа на j

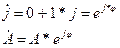
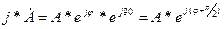 - значит повернуть вектор на 90град. против часовой стрелки

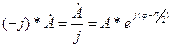- значит повернуть вектор на 90град. по часовой стрелки