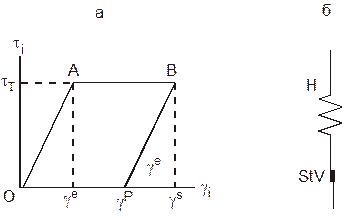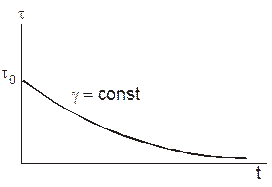ГОРНАЯ ПОРОДА – ОБЪЕКТ РАЗРУШЕНИЯ
Модель горной породы необходимо создавать в соответствии с изучаемой проблемой, т.е. сохранять в модели только те свойства горной породы, которые имеют непосредственное отношение к исследуемому вопросу. Так как нас интересует механическое разрушение горных пород, то и обращать внимание, определяя понятие «горная порода», мы будем на то, что оказывает определяющее влияние на развитие разрушения.
Горная порода – это гетерогенная система, состоящая из частиц твердой фазы, представленной минералами-диэлектриками, полупроводниками, проводниками, жидкой фазы, создающей токопроводящие каналы между частицами твердой, жидкой и газовой фаз, находящихся в порах и полостях трещин.
Одноосное сжатие
s1 > 0, s2 = s3 = 0 и e1 > 0, e2 = e3 = – ne1,
где n – коэффициент поперечной деформации.
Одноосное растяжение
s1 = s2 = 0, s3 < 0 и e1 = e2 = – ne3.
Чистый сдвиг
s1 = – s3 = t, s2 = 0 и e1 = – e3 = g/2, e2 = 0.
4. Осесимметричное трехосное сжатие (нагружение Кармана)
s1 > s2 = s3 > 0 и e1 > 0, e2 = e3 < 0.
5. Радиальное сжатие (нагружение Бёкера)
s1 = s2 > s3 > 0 и e1 = e2 > 0, e3 < 0.
Всестороннее равномерное сжатие
s1 = s2 = s3 = P и e1 = e2 = e3 = eV/3.
Сжатие без возможного бокового расширения (компрессия)
s1 > 0, s2 = s3 = s1n/(1 – n) и e1 > 0, e2 = e3 = 0.
Трехосное неравнокомпонентное сжатие
s1 ¹ s2 ¹ s3 > 0 и e1 ¹ e2 ¹ e3 > 0.
Подставив в выражения (1 – 4) для величин si, ti, ei, gI , приведенные выше значения главных нормальных напряжений и главных линейных деформаций, получим значения этих обобщенных напряжений, описывающих перечисленные напряженные состояния (табл. 2, 3).
В качестве примера определим значения обобщенных напряжений для чистого сдвига:
1. Второй инвариант тензора-девиатора напряжений
I2(Tнд) = [(s1 – s2)2 + (s2 – s3)2 + (s1 – s3)2] / 6 =
= [(– s3)2 + (–s3)2 + (– s3 – s3)2] / 6 = s32 = t2.
2. Интенсивность нормальных напряжений
si = (3.I2(Tнд))0,5 = (3.t2)0,5 = 30,5t.
3. Интенсивность касательных напряжений
ti = (I2(Tнд))0,5 = t.
4. Среднее нормальное напряжение (гидростатическое сжатие)
sср = (s1 + s2 + s3) / 3 = (– s3 + 0 + s3) = 0;
5. Второй инвариант тензора-девиатора деформаций
I2(Tдд) = [(e1 – e2)2 + (e2 – e3)2 + (e3 – e1)2] / 6 =
[2e1 2 + ( – 2 e1)2] / 6 = g2 / 4,
6. Интенсивность линейных деформаций
ei = 2[ I2(Тдд) ]0.5 / 30,5 = 2 ( g2/4)0.5 / 30.5 = g / 30.5,
7. Интенсивность сдвиговых деформаций
gi = 2[ I2(Тдд) ]0.5 = g,
8.Средняя линейная деформация
eср = (e1 + e2 + e3) / 3 = (–e3 + 0 + e3)/ 3 = 0.
Таблица 2
Значения обобщенных напряжений
| Инвариантная величина | Вид напряженного состояния | |||
| Одноосное сжатие | Нагружение Кармана | Всестороннее сжатие | Нагружение Б ёкера | |
| I2(Tнд) | s12/3 | (s1– s3)2/3 | 0 | (s1– s3)2/3 |
| si | s1 | s1 – s3 | 0 | s1 – s3 |
| ti | s1/30.5 | (s1 – s3)/30.5 | 0 | (s1 – s3)/30.5 |
| sср | s1/3 | (s1+2s3)/3 | Р | (2s1+ s3)/3 |
Таблица 3
Значения обобщенных деформаций
Инвариан тная вели чина
Вид напряженного состояния
При рассмотрении деформирования образцов горных пород, находящихся в различных напряженных состояниях, необходимо обращать внимание на изменение формы образца γi, которое вызывается интенсивностью касательных напряжений ti и изменения объёма образцов ev = 3eср под действием всестороннего давления sср. Изменения формы и объёма совсем не обязательно должны описываться одинаковыми законами.
Сдвиг является основным видом сопротивления горной породы разрушению при её сложном нагружении, поэтому в дальнейшем мы будем использовать чаще величины ti и gi , чем si и eI .
РЕОЛОГИЯ ГОРНЫХ ПОРОД
Фундаментом реологии являются несколько аксиом. Содержащиеся в них утверждения получены экспериментально. При изучении реологии мы будем использовать не сами тензоры напряжений и деформаций, а их инварианты, которые являются суммарной характеристикой изменения объёма и формы деформируемых тел.
Представим, что в нашем распоряжении имеются три шара, сделанные из трех различных материалов: стальной, пластилиновый и водяной. С этими тремя шарами мы проделаем несколько мысленных опытов, ставя перед собой основную задачу: определить вид механического воздействия на шары, способный распознать материалы, из которых сделаны шары.
Сначала рассмотрим падение этих шаров с некоторой высоты на поверхность стола. Еще до проведения такого опыта мы уверенно скажем, что различие в материалах, из которых сделаны шары, никак себя не проявит при падении шаров. Лишь при соприкосновении шаров с поверхностью стола мы обнаружим, что шары сделаны из разных материалов: стальной шар отскочит от поверхности стола, пластилиновый - прилипнет к столу, капля воды растечется по поверхности стола. Соприкосновение шаров с поверхностью стола обнаруживает различное деформирование шаров.
Если внимательно осмотрим шар из пластилина, то легко обнаружим на его поверхности плоскую площадку - результат смятия пластилина при контакте с поверхностью стола. В этом случае говорят, что в пластилиновом шаре возникла остаточная пластическая деформация. На поверхности стального шара такой плоской поверхности не видно, но есть все же основания предполагать её наличие в момент контакта шара с поверхностью стола: после окончания контакта шара со столом сферическая форма стального шара была восстановлена и это явилось причиной отскока шара от поверхности стола. Стальной шар – носитель восстанавливающейся упругой деформации. Поведение водного шара также резко отличается от поведения стального и пластилинового шаров: течение водяного шара по поверхности стола означает наличие у него необратимой вязкой деформации.
Подведём промежуточный итог: действие напряжений, возникающих в шарах при соприкосновении с поверхностью стола, вызывает в них появление деформаций различной природы: в стальном шаре возникает упругая деформация, в пластилиновом шаре - пластическая деформация, а в водяном шаре возникает течение, или, по другому, вязкая деформация.
Обнаружив значительное отличие в поведении трех шаров при проведении простого опыта, мы все же не приблизились к пониманию главного: действие какого напряжения способно отличить материал одного шара от материала другого?
Рассмотрим теперь поведение трех шаров при гидростатическом давлении. Эксперименты показывают, что результатом действия небольшого гидростатического давления sср будет увеличение плотности и уменьшение объёма V шаров в соответствии с уравнением sср = K.eср на величину DV = 3sсрV/K, где K - коэффициент объёмного деформирования (модуль объёмного сжатия). Форма шаров останется неизменной. При снятии давления прежние объём и плотность полностью восстанавливаются. Этот экспериментальный факт лег в основу первой аксиомы реологии.
Сложные реологические тела
При последовательном соединении элементов полная нагрузка t приходится на каждый элемент, входящий в сложное тело:
t = t1 = ... = tn,
а полная деформация, возникающая в теле, складывается из деформаций, возникающих в отдельных составляющих сложное тело элементах:
g = g1 + ... + gn.
При параллельном соединении элементов деформации одинаковы для всех элементов:
g = g1 = ... = gn,
а полная нагрузка t складывается из нагрузок на отдельных элементах:
t = t1 + ... + tn.
Рассмотрим некоторые примеры построения сложных тел.
3.2.1. Упруго-пластическое тело Прандтля. Структурная формула тела Прандтля имеет вид Р = Н — StV. Реологическая диаграмма и механическая модель этого тела приведены на рис. 9. Данное тело при напряжениях, ниже предела текучести ti < tт, деформируется упруго по закону Гука ti = G.gI , а при ti = tт деформируется пластически. У этого тела деформация при разгрузке восстанавливается лишь частично. Общая деформация сдвига gs слагается из упругой ge и пластической частей:
|
Рис. 9. Деформационная кривая тела Прандтля: ge – упругая деформация, gp – пластическая деформация |
gs = ge + gp.
Упругопластическое тело Прандтля представляет собой тело, у которого отсутствует деформационное упрочнение. Для поддержания развития пластической деформации не требуется повышения напряжений ti до значений, превышающих предел текучести tт: достаточно поддерживать напряжения, равные пределу текучести.
|
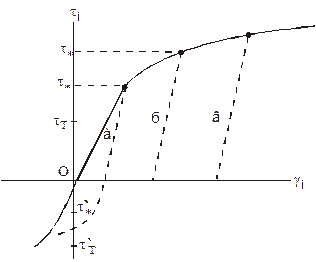
Рис. 10. Деформирование упругопластического тела, обладающего упрочнением
|
На рис.10 приведена зависимость интенсивности касательных напряжений ti от интенсивности сдвиговой деформации gi для упругопластического материала, обладающего деформационным упрочнением. При деформировании такого материала за начальной величиной предела текучести tт в материале начинает накапливаться остаточная деформация gp. Уменьшению напряжений ti на этом участке деформирования соответствует процесс разгрузки, происходящий по упругому закону (пунктирные линии а, б, в, на рис. 10). Новое повышение напряжений ti приводит к увеличению предела текучести до значения t* > tт. Это и есть упрочнение, связанное с развитием пластической деформации.
В таком материале наблюдается и эффект Баушингера: величина обратного (при растяжении материала) предела текучести (упругости) снижается t*' < tт' (рис. 10).
3.2.2. Вязкоупругое тело Максвелла, ползучесть и релаксация напряжений. Структурная формула тела Максвелла М = H — N (рис. 11 а). Реологическое уравнение, соответствующее этой структурной формуле, представляется следующим образом
gM = gH + gN,
где gH, gN – деформация элемента модели тела Гука, Ньютона. Аналогичный вид имеет и формула для скорости сдвиговой деформации в теле Максвелла:
(dgi/dt)M = (dg/dt)H + (dg/dt)N,
где (dg/dt)H, (dg/dt)N - скорость сдвига в телах Гука и Ньютона.
|
Рис. 11. Модели тела Максвелла (а) и тела Пойнтинга–Томсона (б)
|
Подставляя в выражение для скорости сдвиговой деформации тела Максвелла значения скоростей деформаций тел Гука (dg/dt = dt/dt / G) и Ньютона (см. первое уравнение в (8)), получим дифференциальное реологическое уравнение тела Максвелла:
t + Т dτ/dt = h dg/dt (9)
где T = h/ G – время релаксации, dim T = с. Время релаксации T является важным реологическим параметром.
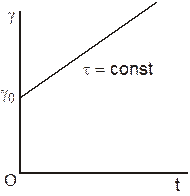
При постоянном напряжении dτ/dt = 0 и тело Максвелла превращается в тело Ньютона, т.е. тело ведет себя как вязкая жидкость. Рост деформации в теле Максвелла с течением времени t происходит по линейному закону
g = tt/h + gо,
|
Рис. 12. Развитие деформации ползучести в теле Максвелла
|
где g о – величина деформации в момент времени t = 0. Этот процесс называется ползучестью (рис. 12).
При постоянной деформации (g = const) решение уравнения (9) имеет следующий вид:
t = tоe–t/T ,
где tо есть начальное напряжение сдвига, t – время действия нагрузки.
|
Рис. 13. Релаксация напряжений в теле Максвелла
|
В соответствии с последним уравнением напряжение в теле Максвелла релаксирует (уменьшаются) практически до нуля (рис. 13).
Скорость развития релаксации напряжений определяется величиной времени релаксации: чем меньше Т, тем в большей степени материал проявляет жидкостные свойства и наоборот, чем больше Т, тем более твердообразным является материал.
Тело Максвелла следует рассматривать, как упруговязкое тело (вязкая жидкость, обладающая упругими свойствами). Проявление твердообразных и вязких свойств тела Максвелла зависит от соотношения времени t действия нагрузки и времени релаксации: если t << T , то в теле возникает, главным образом, упругая деформация и тело ведет себя как тело Гука. Если же справедливо неравенство t >> T, то в теле в большей степени проявляются свойства ньютоновской жидкости и доминирует вязкая деформация.
3.2.3. Тело Пойнтинга–Томсона: РТ = М│H1 (рис.11 б). Структурная формула тела показывает, что в отличие от тела Максвелла в данном случае существует предел деформации, который определяется пружиной H1.
ТЕОРИИ ПРОЧНОСТИ
Под прочностью или трещиноcтойкостью понимается способность твердого тела сопротивляться развитию в нем трещины. Величина прочности оценивается либо значением напряжения, при котором тело разрушается, либо работой деформаций.
Трещины хрупкого разрушения в горных породах следует рассматривать как поверхность разрыва вектора перемещения. На такой поверхности все три компоненты u, v, w этого вектора могут иметь разрыв. Имеется три вида независимых кинематических движений верхней и нижней поверхностей трещины относительно друг друга при разрушении тела: нормальный отрыв, поперечный и продольный сдвиги.
Типы движений противоположных поверхностей трещины, расположенной до деформирования в одной плоскости, можно описать следующим образом:
• нормальный отрыв: две противолежащие поверхности трещины стремятся разойтись симметрично относительно плоскости, в которой была расположена трещина до деформации; между сторонами трещины возникает полость;
• поперечный сдвиг: две противолежащие поверхности трещины скользят одна по другой в одной плоскости, но в противоположных направлениях (срез);
• продольный сдвиг: две противолежащие поверхности трещины в процессе деформирования тела претерпевают кручение в противоположном направлении и оказываются после деформации в различных плоскостях (кручение).
Наиболее опасными с точки зрения развития разрушения являются трещины нормального отрыва. Это связано с тем, что при таком варианте разрушения не происходит потерь энергии, связанных с преодолением сил трения между противоположными поверхностями трещины.
При разрушении на разрыв различают прочность теоретическую и техническую (реальную). Под теоретической прочностью понимают прочность бездефектного твердого тела. В этом случае прочность определяется только величиной энергии связи между частицами (атомы, молекулы) твердого тела. Величина теоретической прочности тела на разрыв (развивается трещина нормального отрыва) составляет примерно одну десятую от значения модуля Юнга: sт = 0,1E = 103 ÷ 104 МПа.
Расчетная величина теоретической прочности некоторых кристаллических минералов: NaCl – 3950 МПа, MgO – 17300 МПа, LiF – 11400 МПа, теоретическая прочность аморфного неорганического стекла составляет 8000 МПа.
Под дефектами твердого тела понимаются любые нарушения кристалллической решетки (внедренные атомы другого вещества и вакансии в узлах кристаллической решетки – это точечные дефекты; дислокации - линейные дефекты; к дефектам относят и механическое повреждение поверхности твердого тела – царапины).
Под технической прочностью понимают прочность реального твердого тела со всеми дефектами. Величина технической прочности значительно (на 2 порядка) меньше теоретической прочности.
Главными дефектами в горной породе, приводящими к значительному понижению их прочности, являются адгезионные границы, трещины и поры. Как следствие этого, реальная прочность горных пород при одноосном растяжении sр невелика (гранит – 11 МПа, порфирит – 17,5 МПа, песчаник кварцевый – 6,6 МПа, известняк – 3,0 МПа).
Если представить трещины и поры в виде эллипса длиной l и радиусом закругления r, то низкое значение технической прочности горных пород при их растяжении можно объяснить следующим образом: в тупиковой части микротрещин (вершине) или пор возникает резкое увеличение действующего напряжения (происходит концентрация напряжений). Если в среднем сечении образца возникает напряжение s*, то в тупиковой части трещины действует напряжение:
sк = 2s*·(l / r)0,5,
величина которого зависит от геометрии дефекта, т.е. от величин l, r.
При уменьшении радиуса кривизны r напряжение sк в вершине трещины возрастает. Тело разрушится тогда, когда напряжение sк достигает величины теоретической прочности sт данного тела.
Прочность образцов горных пород при разрушении их срезом, кручением tсдв, т.е. в тех условиях, когда величина трения между противоположными поверхностями трещины минимальна, превосходит величину прочности, измеряемую при растяжении образцов, но все же значительно меньше величины прочности при одноосном сжатии образцов.
Развитие трещин сдвига существенно затруднено при наличии сил (напряжений), стремящихся прижать две поверхности сдвиговой трещины друг к другу. При этом резко возрастают силы трения (силы внутреннего трения), сдерживающие развитие сдвиговой трещины. Физически это означает появление дополнительного слагаемого (помимо слагаемого, учитывающего действие сил связи в структуре тела), из-за которого и наблюдаются значительные расхождения величины прочности твердых тел при их растяжении и сжатии.
Прочность горных пород при одноосном сжатии sсж многократно превышает величину их прочности sр на разрыв и сдвиговую прочность. Это является следствием не только возникновения внутреннего трения, но и большой неоднородности свойств горных пород. Для более однородных материалов отношение sсж / sр значительно меньше: для чугуна, например, это отношение равно трем, для магниевых сплавов – чуть больше единицы.
Относительные значения величин sсж ,sр , tсдв для некоторых горных пород приведены в табл. 5.
Таблица 5
Рис. 16. Силы, действующие на груз, находящийся на наклонной плоскости
Слагаемое m.s в выражении (12) для t по форме записи аналогично выражению для силы трения на наклонной плоскости, вызванной нормальной реакцией, и по этой причине коэффициент m назван коэффициентом внутреннего трения. Поясним это с помощью рис.16, на котором изображен груз весом G, находящийся на наклоненной под углом j к горизонту плоскости.
При малых значениях угла j груз не в состоянии скользить по плоскости из-за наличия силы трения Fтр между грузом и плоскостью. В этом случае сила трения Fтр превосходит величину силы скольжения Fс.
По определению имеем Fтр = m.Fн, где Fн – нормальная компонента силы G или прижимающая сила, m – коэффициент трения. Движение груза по наклонной плоскости начнется при увеличении угла j и достижении силой скольжения величины силы трения Fс = Fтр .
Величина сил Fн и Fс легко находится через вес груза: Fн = G cosj и Fс = m.Fн. Из равенства m.G ·cos j = G·sin j определим коэффициент внутреннего трения m через угол j :
m = tg j.
Термин «внутреннее трение» следует понимать как способность горной породы повышать сопротивление разрушению под влиянием среднего нормального напряжения сжатия sср, действующего в образце (на плоскости сдвига увеличиваются силы адгезионного взаимодействия между минеральными частицами, растет сила трения).
К физической особенности развития трещин сдвига в горных породах следует отнести образование на плоскости сдвига порошкообразного материала, обладающего высокой дисперсностью.
Наличие жидкости в горной породе изменяет развитие разрушения, т.к. внешняя нагрузка воспринимается уже не только твердым скелетом породы, но и жидкостью, находящейся в порах. Если геометрия порового пространства горной породы обеспечивает дренируемость жидкости, то под действием напора Рn / gж, где Рn – давление жидкости в поре, gж – удельный вес жидкости, произойдет фильтрация жидкости из образца, из очага разрушения. Это вызовет уплотнение породы, при этом все меньшая часть внешней нагрузки будет восприниматься жидкостью. При полном удалении жидкости из образца критерий разрушения будет иметь вид (12), но с несколько иными числовыми значениями слагаемых.
Критерий Кулона–Навье для пористых горных пород, насыщенных недренируемой жидкостью, глин имеет иной вид
t = tо + (sср – Рn)· tg j. (13)
Из уравнения (13) следует, что поровое давление Рn не уменьшает прочность сцепления породы tо, а снижает величину слагаемого, связанного с действием нормального напряжения. Это означает, что рост порового давления создает условия для преждевременного наступления формоизменения, стимулирует сдвиговую неустойчивость горной породы: снижает суммарное сопротивление сдвигу. Подчеркнем, что рассмотренные явления не оказывают влияния на изменение величины коэффициента трения: жидкость, находящаяся в порах под высоким давлением, в развивающихся сколах не служит смазкой. Поровая жидкость является смазкой только в случае проникновения её на адгезионную границу. Заметим, что появление на адгезионных границах жидкости (воды) может происходить вследствие дегидратации минералов, входящих в состав горных пород.
Величина
sср – Рn = sэфф,
входящая в состав второго слагаемого формулы (13), называется эффективным напряжением. Увеличение порового давления обеспечивает снижение напряжения sср, действующего между твердой компонентой горной породы, приводит к снижению эффективного нормального напряжения. Появление эффективного нормального напряжения препятствует закономерному уплотнению горной породы с увеличением глубины залегания пород. Появление аномального уплотнения свойственно горным породам, имеющим большую пористость. В первую очередь, это отличает глинистые горные породы, которые не только имеют большую пористость, но и обладают способностью к образованию связанной воды. Последнее препятствует отжиму воды при сжатии глинистой горной породы. По этой причине критерий Кулона–Навье для глинистых горных пород имеет вид (13).
Условие
Wk = U
является основным при анализе ударного взаимодействия инструмента с горной породой.
Вид функции f(d) зависит как от физико-механических свойств горных пород, так и от геометрии породоразрушающего инструмента. Общий вид функции f(d) к настоящему времени не определен, и это затрудняет проведение математического анализа разрушения горных пород при динамическом нагружении. По этой причине единственным методом исследования процесса разрушения при динамическом нагружении является эксперимент.
Эксперимент показывает, что с увеличением кинетической энергии движущегося тела (использовался ударник цилиндрической формы с плоским основанием) картина разрушения поверхности горной породы качественно выглядит следующим образом. Увеличение скорости соударения вначале приводит лишь к небольшому углублению ударника в поверхность породы: на поверхности образца горной породы виден след ударника в виде остаточной деформации. Под пятном контакта и около него возникает сеть трещин, которая с увеличением скорости соударения становится все гуще.
При определенном значении кинетической энергии W 2 (рис. 29) происходит круговой выкол породы в области, окружающей пятно контакта. Этот вид разрушения называют первой формой разрушения при динамическом нагружении. Основной особенностью первой формы разрушения является резкий рост объема разрушенной горной породы.
С дальнейшим увеличением скорости соударения основной прирост объёма разрушенной породы обеспечивается постепенным внедрением ударника в горную породу. При достижении кинетической энергией значения W 4 наступает вторая форма разрушения: объем разрушенной породы вновь резко возрастает вследствие образования лунки под пятном контакта.
Предполагается, что с дальнейшим ростом кинетической энергии будут наблюдаться и последующие формы разрушения.
Изменение энергоёмкости разрушения. Немонотонное изменение объема горной породы при увеличении скорости соударения определяет и аналогичное изменение удельной объёмной энергоемкости разрушения Аv = Wк / V при динамическом нагружении (рис.29).
Минимальные значения энергоёмкости соответствуют скачкам разрушения горной породы, т.е. тем значениям энергии Wк, при которых она полностью идет на разрушение. При изменении энергоемкости наблюдается следующая закономерность: каждый следующий минимум энергоёмкости Аv меньше предыдущего. При увеличении энергии удара от W2 до W3, от W4 до W5 и т.д. (рис. 29) энергия удара расходуется на упругие деформации горной породы, уплотнение породы и образование в ней зоны предразрушения.
В горной породе под внедрившимся элементом породоразрушающего инструмента выделяют следующие зоны разрушения (рис. 30). В области 1 кроме разрыва адгезионных связей между минералами происходит и разрушение самих минералов.
|
|
Подобный способ разрушения хорош для упругохрупких горных пород. Его можно использовать и для разбуривания упругопластических пород. Но необходимо помнить следующее: для эффективного дробления таких горных пород необходимо повышать скорость соударения, т.к. в этом случае горная порода будет проявлять в меньшей степени свои пластические свойства
6.1.4. Природа динамического действия шарошечного долота. Динамическое воздействие по горной породе забоя скважины реализуется при использованиии любых долот. Исключительно за счет ударной нагрузки разрушаются горные породы при использовании долот дробящего действия. Но для нанесения удара по горной породе забоя скважины вовсе не обязательно использовать долота дробящего действия. Шарошечное долото наносит удары по горной породе забоя скважины при перекатывании шарошки с зуба на зуб, за счет накопления упругой энергии в бурильной колонне и неоднородности горных пород.
Дробящая способность шарошечного долота обеспечивается перекатыванием шарошек по забою с зуба на зуб. Это обеспечивает вертикальное перемещение не только долота, но и всей бурильной колонны. По этой причине на горную породу забоя действует динамическая нагрузка F д во время удара зуба долота по забою, а затем и статическая нагрузка F ст, обеспечивающая дальнейшее внедрение зуба в поверхность забоя. Суммарная нагрузка на забой F S = F д + F ст, отнесенная к величине статической нагрузки, определяет коэффициент динамичности:
k = FS / Fст.
Коэффициент динамичности возрастает с увеличением твердости горной породы, шага зубьев и частоты вращения долота. При разбуривании мягких, средних и твердых горных пород величина коэффициента динамичности принимает следующие значения: 1.1, 1.2, 1.3, соответственно.
Эффективность разрушения горной породы на забое скважины под действием усилий F д , F ст снижается с возрастанием пластических свойств горных пород. Разрушение горных пород на забое глубоких скважин инструментом, вызывающим дробление, обеспечивает малую величину механической скорости.
Под действием ударной нагрузки, превышающей сопротивление горной породы ударному разрушению, происходит ее дробление и образование лунки в результате выкола породы.
И в состоянии устойчивого и неустойчивого положения шарошки под торцом зуба в горной породе возникает напряженное состояние сжатия. Напряжения сжатия в породе достигнет большей величины при опоре шарошки на один зубец. Если при этом возникающие контактные давления превысят сопротивление породы вдавливанию (Pк > H), то горная порода под пятном контакта разрушится, возникнет лунка.
Перекатывание шарошки по забою с зуба на зуб не является единственной причиной появления динамической нагрузки. Так как нагружаемая горная порода забоя скважины практически всегда неоднородна и в каждый момент времени зубья долота находятся в контакте с забоем в разных сочетаниях, то все это приводит к неравномерному разрушению горной породы. При этом возникают колебания с более низкой частотой, но с большей амплитудой, чем при перекатывании шарошки с зуба на зуб.
При работе шарошечного долота различают следующие колебательные процессы, обеспечивающие динамическое воздействие на забой:
а) высокочастотные, появление которых вызвано зубчатостью шарошек,
б) среднечастотные, природа которых связана с изменением во времени числа взаимодействующих с поверхностью забоя скважины зубьев долота,
в) низкочастотные, обусловленные возникновением вследствие неоднородности строения горных пород и их дефектности ухабов на забое скважины.
6.1.5. Природа динамического действия лопастного долота. Лопастные долота также наносят удар по забою в результате накопления упругой энергии в бурильной колонне. В бурильной колонне, являющейся упругим элементом большой протяженности, возникают продольные, крутильные и поперечные колебания.
Виновником возникновения ударной нагрузки является неоднородность свойств горной породы и использование нежесткой бурильной колонны (системы нагружения): в бурильной колонне при бурении накапливается упругая энергия. Через жесткость бурильной колонны упругую энергию, запасенную в ней, можно представить в виде:
W = Df ·j2 + Dl ·d2,
где Dl – продольная жесткость, d – величина абсолютной упругой деформации, Df = Mд / j - угловая жесткость, j - угол закручивания бурильной колонны.
Колебания жесткости в процессе бурения приведут не только к изменению энергии W, но и к изменению углубления долота в горную породу.
Изменение осевой нагрузки на долото, происходящее вследствие возникновения продольных колебаний, может составлять 25 ÷ 50 % и более от величины её среднего значения. Продольные (вертикальные) колебания долота с амплитудой, равной 55 мм, являются обычными. Эти колебания приводят к большим динамическим нагрузкам и являются причиной усталостных поломок элементов бурильной колонны. При прочих равных условиях динамичность будет тем меньше, чем больше число лопастей у долота. На возникновение продольных колебаний значительное влияние оказывает неоднородность прочностных свойств горных пород забоя, наличие трещинноватости в породах.
Под крутильными колебаниями понимают изменение угловой скорости около среднего значения, а под поперечными колебаниями понимают периодические перемещение оси долота по забою.
Природа возникновения крутильных и поперечных колебаний одинакова: неравномерная подача долота и неоднородность механических свойств горных пород забоя, приводящие к неравномерному разрушению породы перед лопастями долота (при одинаковой величине запасенной упругой энергии в бурильной колонне). Это приводит к возникновению крутильных ударов (резкое увеличение момента на долоте) и дополнительному закручиванию бурильной колонны на угол j 1 . При последующем уменьшении подачи происходит уменьшение момента на долоте, при этом буровая колонна раскручивается на угол:
j2 = W1 / M1 – W2 / M2.
Таким представляется механизм возникновения колебаний угловой скорости около среднего значения. Амплитуда и частота колебания зависит как от свойств горной породы, так и от жесткости бурильной колонны. Так как вес бурильной колонны большой, то крутильные колебания вызывают значительные динамические нагрузки на долото в фазе замедления крутильных колебаний. Это может привести к преждевременному повреждению инструмента.
Неоднородность прочностных свойств горных пород приводит к тому, что перед лопастями долота разрушение происходит неодновременно. При этом наблюдается такая картина – вся буровая колонна и долото постоянно смещаются в сторону лопасти, перед которой порода не разрушилась. Это приводит к возникновению поперечных колебаний оси долота. Основная особенность развития поперечных колебаний заключается в том, что скважина приобретает форму многоугольника, число вершин которого на единицу больше числа лопастей долота.
Вдавливании инденторов
Инденторы считаем жесткими, если при внедрении их в поверхность горной породы деформирования самих инденторов не происходит.
При внедрении индентора в полупространство на глубину h под действием силы F образуется контактная площадка диаметром 2а, по которой сила F распределяется в виде давления Р определенным образом. Приведем основные формулы, определяющие заглубление (контактное сближение), радиус контактной площадки и распределение давления в случае контактирования с горной породой, занимающей полупространство, сосредоточенной силы, конуса, цилиндрического индентора и сферы.
Сосредоточенная сила. Если на полупространство действует очень острый нормально приложенный к поверхности индентор (игла), то его действие можно заменить сосредоточенной силой. Впервые решение для случая действия сосредоточенной силы на упругое полупространство было получено Буссинеском.
Конус. Если жесткий конус с углом при вершине 2j внедряется в упругое полупространство с модулем упругости Юнга Е и коэф-фициентом Пуассона n, контактное сближение в центре вдавливания определяется по формуле (контакт конуса с полупространством без трения, конус характеризует большой угол конусности):
,
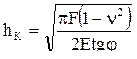радиус контактной площадки
,
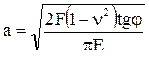развиваемое на контактной площадке среднее давление
.
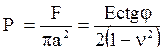Цилиндрический индентор. При внедрении плоского кругового цилиндра диаметром 2а в упругое полупространство сближение определяется по формуле
.
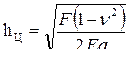Минимальное давление
Рmin = F / 2pa2
будет в центре контакта, а на краях контактной площадки давление неограниченно возрастает. Распределение давления вдоль радиуса контактной площадки представляется выражением
.
СКВАЖИНЫ И ОЧИСТКА ЗАБОЯ
Обеспечение больших механических скоростей при бурении скважин невозможно при несовершенной промывки забоя скважины. Разрушение горной породы, происходящее при бурении, приводит к появлению на поверхности забоя продуктов разрушения – шлама. Плохо организованная промывка забоя скважины приводит к накоплению шлама на забое, происходит зашламование забоя. В этих условиях породоразрушающий инструмент вместо разрушения породы забоя осуществляет вторичное разрушение частиц шлама, происходит переизмельчение шлама.
Лишь при реализации совершенной очистки забоя породоразру-шающие элементы вооружения взаимодействуют не со шламом, рас-положенным на забое, а с неразрушенной горной породой забоя скважины. К реализации совершенной очистки необходимо стремиться. Для этого необходимо совершенствовать и породоразрушающий инст-румент, и промывку забоя скважины.
В реальных условиях бурения почти невозможно избежать переизмельчения уже разрушенной, но не отделенной от поверхности забоя породы. Переизмельчение горной породы в этом случае происходит в присутствии промывочной жидкости (бурового раствора). На раз-рушение шлама (дробление шлама) тратится дополнительная энергия. При дроблении частиц шлама под действием инструмента твердые частицы шлама сначала претерпевают объёмное деформирование (упругое, пластическое) и только после этого происходит разрушение.
Работу, необходимую для дробления шлама, можно разделить на две части: одна часть расходуется на деформирование твердой частицы, а другая – на образование новых поверхностей при разрушении частицы шлама. Работа упругого и пластического деформирования частицы шлама пропорциональна её объёму: Wдеф = k1V, где k1 – коэффициент пропорциональности, равный работе объёмного деформирования единицы объёма частицы шлама, V – объём частицы.
Работа образования новой поверхности при дроблении минерала пропорциональна приращению свежей поверхности:
Wп = γэфф·Δs,
где Δs – прирост свежей поверхности.
Полную работу, затрачиваемую на дробление, можно выразить уравнением Ребиндера П.А.:
W = Wдеф + Wп = kV + γэфф Ds.
Так как объёмное деформирование пропорционально объёму нагружаемого тела V, который пропорционален кубу своего линейного размера, т.е. l3, а изменение поверхности тела пропорционально квадрату линейного размера тела, т.е. l2, то выражение для полной работы дробления можно записать
W = k1l3 + k2l2gо = l2(k1l + k2 γэфф),
где k2 – коэффициент пропорциональности.
Из последнего выражения следует, что при больших размерах тела, т.е. при больших значениях l, можно пренебречь величиной работы образования поверхности. В этом случае
W » k1l3,
т.е. полная работа диспергирования определяется работой упругого и пластического деформирования образца.
При k1 = s сж 2 /2 E из последнего выражения получаем закон дробления Кирпичева–Кика.
При малом линейном размере разрушаемого тела полная работа диспергирования определяется работой, затраченной на образование свежей поверхности:
W » k2l2 γэфф,
так как в этом случае можно пренебречь работой объёмного дефор-мирования диспергируемого тела.
При измельчении частиц шлама на забое при реализации несовершенной очистки забоя частицы шлама разрушаются, в первую очередь, в местах прочностных дефектов (макро- и микротрещины). По этой причине по мере измельчения прочность частиц породы, остающихся на забое, растет (масштабный фактор). Под масштабным фактором понимают изменение прочности образца твердого тела при изменении его размера: чем больше объем образца, тем меньше его прочность. Такое изменение прочности обычно связывают с вероятностью нахождения опасного (т.е. большого по величине) дефекта в теле: чем больше объем образца, тем больше вероятность нахождения в нем опасного дефекта.
Упрочнение горной породы, связанное с масштабным фактором, наблюдается при плохой промывке забоя скважины. Уменьшение размера частиц шлама при переизмельчении горной породы cпособствует росту прочности частиц шлама (масштабное упрочнение). Руководствуясь этим, можно заключить, что энергоёмкость процесса дробления шлама на забое будет зависеть от степени измельчения породы. Увеличение дисперсности шлама на забое скважины при плохо организованной промывке приводит к большому расходу энергии при их дальнейшем дроблении.
По размеру частиц шлама, возникающих в процессе бурения скважины, можно судить, в определенной степени, об эффективности бурения скважины. Преобладание мелкой фракции в продуктах разрушения свидетельствует о плохой промывке забоя и низкой эффективности разрушения горных пород на забое.
Эксперименты и имеющийся опыт бурения показывают, что лучшая очистка забоя и вынос шлама из скважины происходит при следующих значениях сомножителей, определяющих величину удельной гидравли-ческой мощности:
• удельный расход Q/S = (0,35 – 0,7) м3/с·м2;
• величина скорости бурового раствора при истечении из насадков V = (80 – 120) м/с;
• число Рейнольдса в насадках долота должно быть не меньше 105. Другими словами, режим течения бурового раствора под долотом должен быть турбулентным. В этом случае обеспечиваются наиболее благоприятные условия для удаления шлама с забоя и выноса его в кольцевое пространство. Создаются радиальные потоки раствора, увеличива-ющие величину сил, удаляющих шлам с забоя;
• перепад давления на насадках долота должен составлять не менее (50 – 60) % от давления, развиваемого буровым насосом при циркуляции;
• потери давления в кольцевом пространстве скважины должны быть минимальными. Это означает, что режим течения в кольцевом пространстве должен быть ламинарным.
Механическую скорость
Необходимость увеличения механической скорости бурения очевидна. Согласно оценкам, проведенным специалистами Башкирской буровой школы, возрастание V мех в два раза снижает стоимость 1 м проходки на 50 %, увеличение же стойкости долота снижает стоимость 1 м проходки только на 11 %.
Каждый параметр режима бурения (F, n, Q) влияет на эффективность разрушения горных пород по-своему, причем влияние изменения одного из параметров на изменение механической скорости зависит от фиксированной величины других параметров. То или иное значение механической скорости бурения V мех зависит не только от эффективности разрушения горных пород на забое скважины (это лишь одно из условий роста механической скорости), но и от совершенства очистки забоя от шлама, эффективности выноса шлама на поверхность.
8.2.1. Влияние осевого усилия. При механическом способе разру-шения горных пород основная доля энергии расходуется на внедрение породоразрушающих элементов вооружения в горную породу. Величина давления, создаваемого породоразрушающим инструментом на забое скважины, определяется не только величиной осевого усилия F, но и значением контактной площади Sк данного долота. Под контактной площадью понимается сумма площадей всех зубьев на всех шарошках, контактирующих в данный момент с горной породой забоя скважины (для шарошечных долот), сумма площадей торцовой поверхности лопастей (для лопастных долот). Величина контактной площади всех долот (шарошечных, лопастных, алмазных) табулирована, т.е. известна.
При увеличении контактного давления Pк = F / Sк , линейно зависящего от осевого усилия, разрушение на забое происходит по-разному. Рассмотрим три возможных случая:
а) Рк > Н. В этом случае в горной породе, находящейся под пятном контакта, возникает объемное разрушение. Оно характеризуется тем, что возникает при единичном взаимодействии породоразрушающего элемента долота с данной “точкой” поверхности горной породы. Возникающие частицы шлама в этом случае имеют максимальный размер. Разрушение горной породы, происходящее при выполнении приведенного условия, является наиболее эффективным.
Из условия обеспечения объёмного разрушения горной породы величина осевой нагрузки на шарошечное долото рассчитывается по формуле
F = aHSк,
где a = (0,33¸1,59) – коэффициент, учитывающий реальные условия разрушения горной породы в скважине (величину дифференциального давления, температуру горных пород, состояние забоя и пр.), Sк – контактная площадь данного долота. Величина a определяется по промысловым данным.
Зная твердость горных пород и контактную площадь используемого долота, можно определить осевую нагрузку, требуемую для бурения скважины данным шарошечным долотом. Нужно помнить, что по указанной формуле можно определить лишь ориентировочное значение требуемого для разрушения горной породы осевого усилия, т.к. формула не учитывает работоспособность опор долота.
Наблюдающийся экстремальный характер изменения V мех от F связывают с ограничением высоты зубцов на шарошках, наличием шлама на забое. Осевая нагрузка, при которой достигается максимальное значение механической скорости, называется критической.
Следует иметь в виду следующее: при чрезмерном увеличении осевого усилия бурильная колонна теряет устойчивость и претерпевает продольный изгиб, что приводит к незапланированному искривлению скважины.
б) Рк < Н. При такой величине контактного давления возникает усталостно-объемное разрушение горной породы. Непременным следствием установления подобного соотношения между величиной контактного давления и твердостью горной породы является возникновение разрушения при неоднократном действие породоразрушающего элемента вооружения долота на одну и ту же точку забоя. Разрушение при этом связывают с повреждаемостью породы забоя, развитием трещин в горной породе под пятном контакта при каждом ударном цикле нагряжения. Вид лунки выкола такой же, какой возникает при объёмном разрушении.
Количество циклов нагружения n, необходимое для разрушения горных пород, зависит от их механических свойств горной породы: с увеличением хрупкости пород величина n меньше. Зависимость между величиной контактного давления Pк и количеством циклов нагружения n , необходимых для разрушения породы, имеет вид (рис. 37). Эта усталостная кривая описывается уравнением
Ркmn = С,
где m – показатель степени, С = const – постоянная усталостной кривой.
Чем больше Pк, тем меньше необходимо создать циклов нагруже-ния для разрушения горной породы.
|
|
Минимальное контактное давление, вызывающее усталостное раз-рушение при циклическом нагружении при выполнении условия Рк < Н, называется пределом усталости горной породы Рус. Считаетcя, что
Рус = (1/20 ÷ 1/30)H.
Жлобинским Б.А. установлено, что механизм усталостно-объём-ного разрушения горных пород похож на механизм разрушения хрупких горных пород при статическом вдавливании индентора. Лунка выкола возникает вследствие раздробления горной породы под пятном кон-такта, передачи давления от индентора на окружающую породу и возникновения вокруг пятна контакта овальной (если индентор имеет прямоугольную площадку вдавливания) или круглой (при цилиндрическом инденторе) трещины, последняя стадия разрушения связана с раздавливанием уплотненного ядра под индентором и образованием лунки.
в) Рк << Н. Это условие определяет поверхностное разрушение горной породы в результате истирающего действия инструмента. Скорость бурения при выполнении этого неравенства незначительна. Размер частиц шлама мал.
Зависимость механической скорости бурения от величины осевого усилия F (контактного давления Рк) при фиксированной скорости вращения имеет вид (рис. 38).
Представленное на рис. 38 изменение механической скорости бурения от величины осевого усилия указывает на различный механизм разрушения горных пород в трех областях изменения F (или Рк). При малых нагрузках (участок I) зависимость V мех = f ( F ) линейная: прямая выходит из начала координат. Угол наклона прямой к оси F характеризует интенсивность изменения механической скорости при росте осевого усилия. Касательная к кривой, проведенная на участке II, свидетельствует о том, что в этом диапазоне изменения осевого усилия прирост механической скорости больше, чем на первом участке (касательная отсекает от оси F положительный отрезок). На участке III угол наклона касательной меньше, чем на участке II, что свидетельствует о том, что на третьем участке изменение V мех при росте F меньше, чем на втором участке (касательная отсекает от оси F отрезок, расположенный левее начала координат).
Часто зависимость V мех = f ( F ) представляют в виде степенной зависимости
Vмех = кFa.
При a = 1 из этого выражения получаем связь между V мех и F для участка I, при а > 1 – для второго, а < 1 – для третьего участка.
При бурении скважины выбранное значение осевого усилия может обеспечить появление любого из приведенных участков. Рекомендация увеличивать величину осевого усилия F для реализации объемного разрушения не всегда оправдана, т.к., во-первых, часто при больших усилиях начинается интенсивный износ долота, увеличивающий контактную площадь долота, и приводящий к снижению V мех, во-вторых, бурение при меньщих осевых нагрузках, сопровождаемое снижением механической скорости, часто приводит к достижению положительного результата, например, росту проходки на долото, росту рейсовой и коммерческой скорости, снижению себестоимости метра проходки. Cледует иметь в виду, что увеличение осевого усилия приводит к росту интенсивности искривления скважины, это связано с возрастанием отклоняющей силы при увеличении прогиба КНБК, большим разрушением стенки скважины.
Зашламование забоя существенно изменяет зависимость V мех = f ( F ), так как происходит не только снижение V мех , но и уменьшение величины осевого усилия, при котором достигается наибольшее значение механической скорости.
Приведенное на рис. 38 изменение механической скорости отличает не только бурение скважин шарошечным, но и лопастным долотом.
Выбор параметра режима бурения – осевой нагрузки на долото – по диаграмме V мех = f ( F ) не гарантирует от ошибок.
В настоящее время при бурении чаще всего реализуется поверхностное (при турбинном бурении) и усталостно-объемное разрушение горных пород. Связано это, в основном, с тем, что материал, из которого изготавливается породоразрушающий инструмент, меньше изнашивается при реализации усталостно-объёмного разрушения.
Контроль за величиной F при бурении скважины реализуется с помощью индикаторов веса гидравлических (ГИВ), электрических (ЭИВ), которые устанавливаются на неподвижном конце талевого каната.
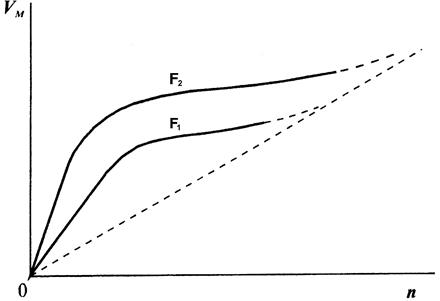
8.2.2. Влияние частоты вращения долота. Общий вид зависимости V м = f ( n ) хорошо известен из работ В.С.Федорова (рис.39). На кривой выделяются два линейных участка: начальный и конечный. На этих участках Vм изменяется пропорционально n, что свидетельствует о постоянстве проходки за оборот d.
Основными факторами, определяющими вид кривой Vм = f ( n ), являются следующие:
• время контакта t к зуба шарошечного долота с горной породой,
• число поражений забоя зубьями долота.
С увеличением частоты вращения n возрастает число поражений забоя зубьями шарошечного долота, возрастает скорость и энергия соударения. Это обеспечивает рост механической скорости бурения. Но одновременно с этим увеличение n обеспечивает и снижение времени контакта t к , что снижает эффективность разрушения горных пород и, как следствие, механическую скорость. В результате действия указанных факторов при бурении возникает сложная зависимость V м = f ( n ).
|
Рис. 39. Общий вид зависимости Vм = f(n) при различных осевых усилиях (F2 > F1) |
На участке кривой Vм = f(n), расположенном между начальным и конечным линейными участками, изменение механической скорости, происходящее при постоянной осевой нагрузке, но росте частоты вращения, характеризуется снижением темпа прироста механической скорости. При определенной частоте вращения nкр наблюдается резкое снижение темпа прироста механической скорости. Это происходит вследствие резкого уменьшения глубины внедрения зуба долота в горную породу за один оборот, снижения времени контакта зуба долота с забоем скважины. Для мрамора, например, nкр = 100 мин-1. С ростом твердости горной породы nкр возрастает.
Энергоемкость разрушения возрастает. По этой причине бурение скважины с частотой вращения n > nкр нерационально. При данном значении осевого усилия увеличение n долота с целью повышения механической скорости целесообразно лишь до тех пор, пока возрастает рейсовая скорость бурения.
Обладая технологической информативностью, зависимость Vм = f(n), тем не менее, не может быть гарантом выбора рекомендуемого значения частоты вращения n. Тому есть причина: отсутствие приборов, надежно контролирующих частоту вращения. В роторном бурении частота вращения долота равна частоте вращения ротора и может быть измерена тахометром достаточно точно. Для измерения частоты вращения долота в турбинном бурении используется турботахометр, датчик которого устанавливается в верхнем узле турбобура и соединяется с валом последнего. Работа турботахометра основана на фиксации специальной аппаратурой, устанавливаемой на вертлюге, импульса давления, формируемого при кратковременном перекрытии трубного пространства через каждые 10 оборотов вала турбобура. Каналом связи служит промывочная жидкость, находящаяся внутри бурильной трубы. Особенностью гидравлического канала связи является существенное затухание энергии сигнала в связи с потерями на трение у стенок колонны и наличие помех, создаваемых работающим буровым насосом.
С увеличением глубины скважины в большей степени проявляются пластические свойства горных пород, требуются большие деформации до разрушения и большая длительность контакта зубьев долота с забоем. Это вызывает необходимость снижения частоты вращения долота с углублением скважины. Существует и другая причина, по которой необходимо снижать величину n при росте глубины скважины. Значительный рост мощности, необходимой для привода ротора из-за роста потерь на трение бурильной колонны о стенку скважины.
Частота вращения инструмента оказывает существенное влияние на качественный отбор керна.
8.2.3. Влияние интенсивности промывки забоя скважины. Циркуляция промывочной жидкости при бурении скважины должна обеспечить очистку забоя от частиц разрушенной горной породы, предотвратить вторичное перемалывание этих частиц. Именно по этой причине проектирование режима очистки забоя скважины промывочной жидкостью является составной частью проектирования параметров режима бурения.
С возрастанием расхода Q улучшается очистка забоя, следовательно, повышается эффективность работы долота. Но в то же время увеличиваются потери давления в кольцевом пространстве пропорционально Q 2. Это приводит к росту гидродинамического давления на забой, создаются неблагоприятные условия для отрыва шлама от поверхности забоя, снижается механическая скорость бурения. Другими словами, отрицательным последствием интенсификации промывки скважины может стать увеличение дифференциального давления на забое скважины и, как следствие, ухудшение условий разрушения горной породы.
Отмеченное двоякое влияние производительности циркуляции промывочной жидкости на скорость бурения отражено формулой, предложенной В.С. Федоровым:
Vм = Q /(a + bQ),
где a, b – параметры, зависящие от свойств разбуриваемых горных пород, промывочной жидкости, размеров кольцевого канала (рис. 40).
Для улучшения очистки забоя скважины следует стремиться не к бесконечному увеличению производительности циркуляции, а добиваться этого использованием насадков уменьшенных диаметров, приближенных к забою, созданием радиальных турбулентных потоков промывочной жидкости вдоль поверхности забоя, обеспечивающих отрыв частиц шлама от забоя, введением в промывочную жидкость смазывающих добавок, снижающих величину сил, удерживающих частицы шлама на забое и пр.
Согласно исследованиям отечественных ученых, удельный расход промывочной жидкости, подаваемой на забой скважины, для шарошечных и лопастных долот должен составлять (0,057 ÷ 0,065) л/(с·см2), и для алмазных – (0,06 ÷ 0,1) л/(с·см2).
Особо подчеркнем, что увеличение механической скорости бурения применением гидромониторных насадков обеспечивается не дополнительным разрушением горной породы забоя высоконапорными затопленными струями промывочной жидкости, а улучшением очистки забоя от шлама при использовании гидромониторных насадков. Для успешного механогидравлического воздействия на горную породу забоя скважины и разрушения горной породы струей жидкости, вытекающей из насадков, необходимо значительно увеличить скорость истечения затопленной струи из насадков (довести скорость истечения струи до нескольких сотен метров в секунду), воздействовать струей на ту часть площади забоя, на которую воздействует зуб долота.
При бурении мягких горных пород повышение расхода промывочной жидкости приводит к размыву стенки скважины, что может обеспечить рост интенсивности искривления скважины. Введение в промывочную жидкость смазывающих добавок снижает трение инструмента о горную породу стенки скважины, что способствует меньшему ее разрушению и обеспечивает меньшее искривление скважины.
Завершая разговор о влиянии расхода промывочной жидкости на величину механической скорости, отметим, что практика бурения скважин с высокими механическими скоростями (свыше 10 – 15 м/ч) в Западной Сибири обнаружила влияние “утяжеления” восходящего потока промывочной жидкости с увеличением концентрации шлама в ней на величину механической скорости. Это позволяет ставить задачу оптимизации расхода промывочной жидкости с целью минимизации гидродинамического давления на забой скважины.
Измерение расхода промывочной жидкости осуществляется индукционными расходомерами РГР-7, РГР-100, принцип действия которых основан на явлении электромагнитной индукции и обеспечивает контроль расхода только электропроводящей промывочной жидкости.
Горных пород при бурении
ЗАКЛЮЧЕНИЕ
Механический способ разрушения горных пород при бурении скважин к настоящему времени далеко себя не исчерпал. Его дальнейшее развитие связано как с совершенствованием бурового инструмента, повышением эффективности разрушения горной породы ударной нагрузкой, вдавливанием, сдвигом, применением новых износостойких материалов, так и с совершенствованием технологии бурения.
Повышение эффективности разрушения горных пород на забое скважины следует связывать со способностью инструмента усиливать естественное развитие остаточной деформации в горной породе под пятном контакта, с возможностью создания сдвиговой неустойчивости горных пород забоя скважины, с совершенствованием очистки забоя от разрушенной горной породы.
СПИСОК ЛИТЕРАТУРЫ
1. Баклашов И.В., Картозия Б.А. Механика горных пород. – М.: Не-дра. – 1975.
2. Войтенко В.С. Управление давлением при бурении скважин. – М.: Недра. – 1986.
3. Ганджумян Р.А., Калинин А.Г., Никитин Б.А. Инженерные расчеты при бурении скважин: Справочное пособие / Под ред. А.Г.Ка-линина. – М.: Недра, 2000.
4. Евсеев В.Д. Разрушение горных пород при различных напряженных состояниях: Учебное пособие. – Томск: Ротапринт ТПУ. – 2000.
5. Крупенников Г.А., Филатов Н.А. Распределение напряжений в породных массивах. – М.: Недра. – 1972.
6. Мавлютов М. Р. Разрушение горных пород при бурении скважин. – М.: Недра. – 1978.
7. Осипов П.Ф., Скрябин Г.Ф. Оптимизация режимов бурения гидромониторными шарошечными долотами. – Ярославль: Медиум-пресс. – 2001.
8. Основы бурения нефтяных и газовых скважин: Учебное пособие / А.Г.Калинин, В.С. Литвиненко, А.И. Радин. – Санкт-Петербург: Гос. горный ин-т. – 1996.
9. Павлова Н.Н. Деформационные и коллекторские свойства горных пород. – М.: Наука. – 1975.
10. Попов А.Н., Головкина Н.Н. Прочностные расчеты стенок сква-жины в пористых горных породах: Учебное пособие. – Уфа: Изд-во УГНТУ, 2001.
11. Протасов Ю.И. Разрушение горных пород. – М.: Изд-во МГГУ, 2001.
12. Процессы разрушения горных пород и резервы повышения скоростей бурения / Колесников Н.А., Рахимов А.Е., Брыков А.А., Булатов А.И. – М.: Недра. – 1989.
13. Ржевский В.В., Новик Г.Я. Основы физики горных пород. – М.: Недра. – 1984.
14. Спивак А.И., Попов А.Н. Разрушение горных пород при бурении скважин. – М.: Недра. – 1994.
15. Сулакшин С.С. Разрушение горных пород: Учебное пособие. – Томск: Ротапринт ТПУ. – 1994.
16. Сулакшин С.С. Бурение геолого-разведочных скважин: Справочное пособие. – М.: Недра. – 1991.
17. Эйгелес Р.М. Разрушение горных пород при бурении. – М.: Недра, 1971.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ …………………………………………………………….… 3
1. ГОРНАЯ ПОРОДА – ОБЪЕКТ РАЗРУШЕНИЯ ………………… 4
1.1. Характеристика сил связи в структуре горной породы………. 4
1.2. Классификация горных пород академика Сергеева Е.М………. 7
1.3. Твердая компонента горной породы……………………………. 7
1.4. Жидкая компонента горной породы …………………………… 9
1.4.1. Состояние воды в горной породе ………………………… 10
1.5. Пористость и проницаемость горных пород ………………… 11
1.6. Горная порода как многокомпонентная система ……………… 13
2. ГОРНАЯ ПОРОДА – СПЛОШНАЯ СРЕДА …………………… 15
2.1. Напряженно-деформированное состояние горных пород…….. 15
2.1.1. Напряженное состояние в «точке» …………………………. 15
2.1.2. Вектор перемещения и деформированное состояние
в «точке» …………………………………………………………….. 21
2.2. Инвариантные соотношения для напряжений и
деформаций при различных напряженных состояниях ………… 27
2.3. Энергия изменения формы и объёма при деформировании… 29
2.4. Геометрическая интерпретация напряженного состояния……. 31
3. РЕОЛОГИЯ ГОРНЫХ ПОРОД ……………………………………. 34
3.1. Аксиомы реологии. Виды идеальных деформаций……………. 36
3.2. Сложные реологические тела …………………………………… 41
3.2.1. Упругопластическое тело Прандтля………………………… 41
3.2.2. Вязкоупругое тело Максвелла, ползучесть и релаксация
напряжений …………………………………………………… 43
3.2.3. Тело Пойнтинга–Томсона …………………………………… 45
3.3. Особенности ползучести горных пород ……………………….. 45
3.4. Реологические параметры, модули деформации и их
определение ……………………………………………………… 47
3.4.1. Модуль Юнга – модуль продольной упругости ………….... 48
3.4.2. Коэффициент поперечной деформации ……………………. 50
3.4.3. Коэффициент объемного деформирования ………………… 51
4. ТЕОРИИ ПРОЧНОСТИ …………………………………………….. 52
4.1. Механическая теория прочности Кулона ……………………… 55
4.2. Механическая теория Кулона-Навье …………………………… 56
4.3.Энергетическая теория прочности Гриффита А.А. ……………. 59
4.3.1. Эффект Иоффе А.Ф. ………………………………………… 60
4.3.2. Эффект Ребиндера А.П. …………………………………… 61
4.4. Кинетическая теория прочности ……………………………… 62
5. ДЕФОРМАЦИОННОЕ ПОВЕДЕНИЕ ГОРНЫХ ПОРОД ПРИ РАЗЛИЧНЫХ НАПРЯЖЕННЫХ СОСТОЯНИЯХ ……..… 64
5.1. Развитие разрушения и определение прочности при
одноосном растяжении и сжатии образцов горных пород …….…65
5.1.1. Определение прочности при одноосном растяжении ….… 66
5.1.2. Определение прочности при одноосном сжатии …………... 67
5.1.3. Влияние трения на торцовых поверхностях на
разрушение образцов и их прочность ……………………………... 68
5.1.4. Влияние жесткости системы нагружения на развитие разрушения……………………………………………………….….. 70
5.2. Разрушение образцов горных пород при трехосном сжатии….. 73
5.2.1. Разрушение образцов горных при всестороннем
равнокомпонентном сжатии……………………………………….. 73
5.2.2. Разрушение образцов при осесимметричном
трехосном сжатии. Дилатансия ………………………………… 75-76
НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН
Учебное пособие
Редактор Р.Д.Игнатова
Подписано к печати 27.12.2004.
Формат 60×84/16. Бумага офсетная.
Печать RISO. Усл.печ.л. 8,78. Уч. изд.л. 7,95.
Тираж 300 экз. Заказ . Цена свободная.
Издательство ТПУ. 634950, Томск, пр.Ленина, 30.
ГОРНАЯ ПОРОДА – ОБЪЕКТ РАЗРУШЕНИЯ
Модель горной породы необходимо создавать в соответствии с изучаемой проблемой, т.е. сохранять в модели только те свойства горной породы, которые имеют непосредственное отношение к исследуемому вопросу. Так как нас интересует механическое разрушение горных пород, то и обращать внимание, определяя понятие «горная порода», мы будем на то, что оказывает определяющее влияние на развитие разрушения.
Горная порода – это гетерогенная система, состоящая из частиц твердой фазы, представленной минералами-диэлектриками, полупроводниками, проводниками, жидкой фазы, создающей токопроводящие каналы между частицами твердой, жидкой и газовой фаз, находящихся в порах и полостях трещин.
Дата: 2019-07-30, просмотров: 206.
