Выявив риски, можно перейти к их анализу. Он может быть качественным (выявление факторов, областей и видов рисков) и количественным. Последний позволяет в численной форме оценить размеры отдельных рисков и проекта в целом.
Ранее уже были рассмотрены некоторые способы анализа инвестиций с поправкой на риск: использование ставки дисконтирования с поправкой на риск, использование коэффициентов поправки на риск в методе состояния предпочтения. Попробуем дать общую оценку рисков.
Методы количественного анализа рисков:
1. Метод аналогий: заключается в использовании информации о других (ранее выполненных проектах), о деятельности конкурентов и т. д.
2. Анализ чувствительности: он позволяет определить предельные значения факторов риска, при которых результаты окажутся приемлимыми (как изменятся NPV, IRR при росте цен на материалы, при повышении прямых, общих издержек, падении цены продаж, изменении уровня налогообложения).
Анализ чувствительности в итоге помогает определить:
- Факторы, наиболее сильно влияющие на интегральные показатели проекта;
- Варианты достижения поставленных целей, наиболее устойчивые к рискам.
Данный подход достаточно неплохо реализован в программе Project Expert и дает первоначальную пищу для размышлений.
1. Анализ сценариев- предполагает составление полного перечня всех возможных вариантов развития событий и оценку вероятностей осуществления каждого из них. Преимущество метода- возможность учета корреляции между разными рисками и оценки одновременного влияния нескольких факторов риска на результаты проекта. Из-за субъективности и сложности определения вероятностей события часто поступают проще: для каждого показателя определяют пессимистическое, оптимистическое и наиболее вероятное значение и рассчитывают матожидание с весами 1:1:4.
2. Метод Монте-Карло- метод формализованного описания риска, отражающий всю гамму неопределенности. В основе метода:
- Построение модели, отражающей зависимость результатов от исходных данных;
- Выявление ключевых факторов риска;
- Нахождение параметров вероятностного распределения факторов риска и выявление корреляционной зависимости между этими параметрами;
- Генерирование множества сценариев при ключевых факторах риска;
- статанализ результатов (матожидание, дисперсия и т. д.).
Фактически, в основе метода Монте-Карло применены имитационные модели, необходимые для сложных проектов, характеризующихся возможностью многообразных решений. Построить имитационную модель можно на основе дерева решений. Дерево решений основывается на том, что оценивается вероятность отдельных этапов проекта и определяются все возможные пути по дереву решений, причем закон распределения издержек, цен и объемов продаж может отличаться от нормального (логнормальное, потенциальное). Риск в этом случае учитывается через вероятности и взвешенный интегральный эффект будет равняться сумме произведений вероятности пути по дереву решений и эффекту инвестора для исхода при пути по данному дереву решений по ставке безрискового вложения: 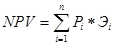 , где
, где
n- число путей по дереву решений,
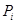 - вероятность i-пути,
- вероятность i-пути,
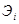 - эффект для инвестора для i-пути.
- эффект для инвестора для i-пути.
Как видно, модель дерева решений имеет нечто общее с методом достоверных эквивалентов.
Дерево решений и есть имитационная модель, только где варианты характеристик инвестиционного проекта являются случайными величинами. Поэтому:
1) Основные характеристики проекта, заложенные в него, принимаются за случайные величины (цены, объем продаж, величина инвестиций, переменные и постоянные издержки, время НИОКР и подготовки пр-ва и т.д.). Матожидания случайных величин есть детерминированнные оценки и модель учитывает взаимосвязь некоторых переменных, например:
а) Взаимосвязь цены и объемов продаж характеризуется :
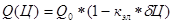 , где
, где
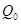 - объем продаж инвестиционного продукта, соответствующий матожиданию цены,
- объем продаж инвестиционного продукта, соответствующий матожиданию цены,

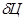 - относительное изменение цены,
- относительное изменение цены,
к- коэффициент эластичности спроса по цене
б) зависимость издержек от объемов производства
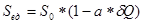 , где
, где
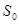 - издержки инвестиционного продукта, соответствующие матожиданию объема продаж,
- издержки инвестиционного продукта, соответствующие матожиданию объема продаж,
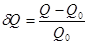 - относительное изменение объема продаж,
- относительное изменение объема продаж,
a- постоянный коэффициент, зависящий от структуры издержек.
2) Могут быть выдвинуты приемлимые гипотезы о характере распределения переменных и параметрах этих распределений.
Например:
Таблица 2.16
| Случайная переменные | Вид распределения | Пределы распределения |
| Цена | Нормальное | 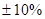
|
| Объем продаж | Логнориальное | +10%+-5% |
| Прямые издержки | Потенциальное | +10%+-15% |
1) Проект реализуется в условиях свободного рынка.
2) Лучше, если дерево решений имеет детерминированную структуру.
Итого, задавая случайные размеры переменных, удовлетворяющие требованиям п.п. 1-4, получают значения NPV и вероятности их получения. Имитационная модель чаще всего имеет вид гистограммы, где по оси абцис- NPV, а по оси ординат- вероятность этих NPV. Риск рассчитывается исходя из статанализ результатов (матожидание, дисперсия, коэффициент вариации).
1. Экспертные методы
Самый простой способ:
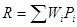 , где
, где
R- степень рискованности проекта,
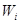 - значимость риска для результата проекта,
- значимость риска для результата проекта,
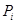 - вероятность появления риска.
- вероятность появления риска.
Кроме того, эксперт может использовать следующую шкалу оценки рисков:
Таблица 2.17
Шкала оценки факторов риска
| Качественная оценка риска | Балл |
| Высокий: вероятно, риск реализуется | 10 |
| Выше среднего: скорее всего, риск реализуется | 7 |
| Средний | 5 |
| Ниже среднего: скорее всего, риск не реализуется | 3 |
| Низкий, несущественный | 1 |
Эксперт имеет возможность качественно оценить вид или фактор риска и обобщить риск по проекту:
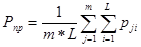 , где
, где
m- количество оцениваемых рисков;
L- число экспертов;
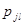 - балловая оценка j-риска L-инвестором.
- балловая оценка j-риска L-инвестором.
Риск проекта оценивается по следующей таблице.
Таблица 2.18
Значение 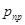
| Уровень риска |
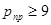
| Высокий |
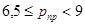
| Выше среднего |
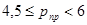
| Средний |
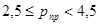
| Ниже среднего |
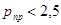
| Низкий |
Здесь же имеет смысл ввести понятие ставки дисконтирования с учетом риска по методу наращения. Метод применим когда когда дерево ветвей не имеет большого разнообразия, а распределение вероятностей- нормально при малой дисперсии.
Норма дисконта по методу наращения означает, что ставка дисконтирования зависит не только от фазы, но и от этапа реализации проекта и нома дисконта для этапа проекта равна: 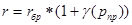 , где
, где
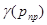 - коэффициент роста безрисковой ставки для данной
- коэффициент роста безрисковой ставки для данной 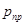 для данного этапа (определяется экспертным путем).
для данного этапа (определяется экспертным путем).
Управление рисками в самом общем виде включает в себя:
· Получение дополнительной информации;
· Распределение риска между участниками проекта;
· Резервирование средств;
· Диверсификация.
Вопрос управления рисками реальных инвестиций предлагается решать на этапе экономической оценки инвестиций путем оценки степени риска и одобрения проектов с приемлимым уровнем риска.
Список использованной литературы.
1. Стратегической планирование инвестиционной деятельности.
2. Анализ экономической эффективности.
3. Бирман Г., Шмидт С. Экономический анализ инвестиционных процессов. М.: Юнити, 1997.
4. Под ред. Данилочкиной. Контроллинг как инструмент управления финансами. М.: Юнити, 1998.
5. В. В. Ковалев. Финансовый анализ. Управление капиталом. Выбор инвестиций. Анализ отчетности. М.: Финансы и статистика, 1998.
6. Под ред. Терехина В. И. Финансовое управление фирмой. М.: Экономика, 1998.
Дата: 2019-07-30, просмотров: 327.