Метод состояния предпочтения- более сложный и тонкий инструмент. Если достоверный эквивалент равен математическому ожиданию денежных потоков, то ценность денег зависит исключительно от вероятности наступления каждого возможного состояния природы. Напротив, в основе метода состояния предпочтения лежит предположение о различной полезности денежных потоков для предприятия в различных ситуациях.
Использовать метод предпочтительного состояния при разработке капитального бюджета в условиях неопределенности с теоретической точки зрения настолько же правильно, как и применять метод текущей стоимости в условиях определенности. Методы текущей стоимости и предпочтительного состояния тесно взаимосвязаны. Можно представить себе, что метод предпочтительного состояния- это обобщение метода текущей стоимости для случая неопределенности.
В модели предпочтительного состояния трактовка неопределенности следующая: пусть в период 0 доллары в условиях В дороже, чем доллары в условиях А. Более высокая цена может отражать тот факт, что предельная ценность доллара для потребителя в условиях В больше, чем в условиях А (так как предельная полезность того, что на него можно купить, больше). Другое возможное объяснение заключается в том, что средний инвестор считает низкой вероятность возникновения условий А и потому не хочет платить высокую цену за доллары, которые он получит только в этих условиях. На условные коэффициенты текущей стоимости влияют и недостаточность долларов в некоторых условиях, и вероятность самого этого состояния.
Применяется метод предпочтительного состояния следующим образом:
Сначала составляют список всех возможных "состояний природы" на каждый период времени. Здесь "состояние природы"- это денежные поступления за период. Для каждого такого состояния рассчитывают коэффициент, показывающий, чему равна ценность одной денежной единицы в данном состоянии природы. Этот коэффициент называется коэффициентом приведенной стоимости с поправкой на риск. Он представляет собой произведение трех сомножителей: RAPVE= 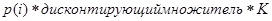 .
.
Ценность одной денежной единицы в i-м состоянии природы (RAPV)= 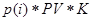 =
= 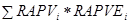 , где
, где
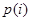 - вероятность того, что состояние наступит (сумма вероятности по всем событиям должна равняться 1), PV- приведенная стоимость достоверного дохода в одну денежную единицу. и К — коэффициент поправки на риск при данном состоянии, т.е. количественное выражение полезности риска для предприятия:
- вероятность того, что состояние наступит (сумма вероятности по всем событиям должна равняться 1), PV- приведенная стоимость достоверного дохода в одну денежную единицу. и К — коэффициент поправки на риск при данном состоянии, т.е. количественное выражение полезности риска для предприятия:
То есть денежные потоки для каждого состояния природы умножают на коэффициент ценности доллара в соответствующем состоянии природы и на вероятность самого по себе состояния природы. Сумма полученных произведений- это ценность предлагаемого инвестиционного проекта.
Коэффициент поправки на риск помогает учесть различную ценность денег в разных условиях (например, в условиях кризиса предприятию дорога каждая копейка, а в условиях процветания- можно рискнуть значительной суммой). Чем выше коэффициент поправки на риск, тем больше ценность денег в данном "состоянии природы. Таким образом, можно ожидать, что коэффициент поправки на риск будет ниже среднего при условии, что доход и богатство большинства инвесторов выше среднего и выше среднего, если доход и богатство большинства инвесторов ниже среднего. Требуется понимание того, что коэффициенты поправки на риск, связанные с некоторым состоянием, зависят от дохода и богатства типичного инвестора в этом состоянии в один и тот же период времени. Если же величина активов относительно невелика, коэффициент не зависит от суммы денег, генерируемых активом в этом состоянии (если денежные потоки этого актива составляют малую часть доходов типичного инвестора).
Весьма интересна ситуация “противофазных активов”, когда инвестиции генерируют более высокие суммы доходов в тех ситуациях, когда деньги особенно нужны.
Итак, каждое событие характеризуется собственным коэффициентом поправки на риск. Эти коэффициенты просто отражают цену долларов в различных событиях, но за один период и не учитывают стоимость денег во времени и вероятность наступления события.
Пример.
Таблица 2.13
| Вариант | Вероятность варианта | NPV (20%) | Коэффициент поправки на риск (К) | NPV с поправкой на риск |
| Вариант А | 0,2 | 6,79 | 2 | 2,72 |
| Вариант Б | 0,6 | 21,10 | 1 | 12,66 |
| Вариант В | 0,2 | 9,07 | 2,5 | 4,53 |
Дстоверный эквивалент
Модель предпочтительного состояния предполагает, что все инвесторы пришли к согласию, во-первых, относительно состояния природы, которые в принципе возможны и во-вторых, о сегодняшней ценности одной денежной единицы, которая будет получена в каждом из состояний. Если все договоряться и по поводу денежных потоков, возникающих в каждом из состояний, то будет выработано общее мнение и о ценности активов.
Инвесторы могут договориться о значениях коэффициентов приведенной стоимости с поправкой на риск для каждого состояния природы, если существуют рынки, на которых условные (зависящие от состояния природы) денежные потоки можно “купить” или “продать” по отдельности. Если такие рынки есть, то можно сделать инвестиционные вложения в такой портфель активов, который приносит оптимальное количество долларов в каждом состоянии в зависимости от бюджетных ограничений предприятия.
Кроме того, найдя RAPVE для нескольких периодов, мы должны учитывать, что их можно использовать для оценки множества различных активов (то есть для других инвестиционных проектов).
Метод предпочтителъного состояния математически красив и теоретически верен, а потому его использование в анализе инвестиционных проектов представляется целесообразным.
Недостатки метода:
• для сложного проекта трудно составить перечень всех возможных состояний природы;
• метод требует большого объема вычислений, даже если расчеты производят при помощи компьютера;
• не всегда можно объективно определить ценность денег в каждом состоянии природы;
• человеку психологически трудно оценивать вероятности.
Таким образом, для применения метода предпочтительного состояния необходимо выявить условия возникновения денежных потоков, определить денежные потоки в каждом из условий и найти коэффициенты текущей стоимости с поправкой на риск.
Кроме того, метод дает возможность сравнить относительную рискованность двух или более проектов: проект, который предлагает защиту от возможных потерь (то есть имеет денежные потоки большей стоимости), относительно более привлекателен.
Но есть, которые недостатки затрудняют использование метода достоверных эквивалентов в проектировании инвестиционных проектов: трудность определении RAPVE при отсутствии совершенных рынков.
3. Анализ методов принятия решений без использования численных значений вероятностей. На практике часто встречаются ситуации, когда оценитъ значение вероятности собьггия чрезвычайно сложно. В этих случаях часто применяют методы, не использующие численные значения вероятностей:
• максимакс- максимизация максимального результата проекта;
• максимин- максимизация минимального результата проекта;
• минимакс- минимизация максимальных потерь;
•компромиссный- критерий Гурвица: взвешивание минимального и максимального результатов проекта.
Для принятия решений об осуществлении инвестиционньгх проектов строят матрицу. Столбцы матрицы соответствуют возможным "состояниям природы"- ситуациям, над которыми руководитель предприятия не властен. Строки матрицы соответствуют возможным альтернативам осуществления инвестиционного проекта- "стратегии", которые может выбрать руководитель предприятия. В клетках матрицы указываются результаты каждой стратегии для каждого состояния природы.
Пример. Предприятие анализирует инвестиционный проект строительства линии по производству нового вида продукции. Существует две возможности: построить линию большой мощности или построить линию малой мощности. Чисгая приведенная стоимость проекта зависит от спроса на продукцию, а точный объем спроса неизвестен, однако известно, что существует три основных возможности: отсутствие спроса, средний спрос и высокий спрос. В клетках таблицы показана чистая приведенная стоимостъ проекта в соответствующем .состоянии природы при условии, что предприятие выберет соответствующую стратегию. В последней строке показано, какая стратегия оптимальна в каждом состоянии природы.
Таблица 2.14
Пример построения матрицы стратегий н состояний природы для инвестиционного проекта:
| Стратегия | Состояние природы | ||
| Отсутствие спроса | Средний спрос | Высокий спрос | |
| Построить линию малой мощности | - 100 | 150 | 150 |
| Построить линию большой мощности | -200 | 200 | 300 |
| Оптимальная стратегия для данного состояния природы | Построить линию малой мощности | Построить линию большой мощности | Построить линию большой мощности |
Максимаксное решение - построить линию большой мощности: максимальная чистая приведенная стоимость при этом составит 300, что соответствует сотуации высокого спроса. Максимаксный критерий отражает позицию руководителя-оптимиста, игнорирующего возможные потери.
Максиминное решение - построить линию малой мощности: минимальный результат этой стратегии- потеря 100 (что лучше, чем возможная потеря 200 при строительстве линии большой мощности). Максиминный критерий отражает позицию руководителя, совершенно не склонного рисковать и отличающегося крайним пессимизмом. Этот критерий весьма полезен в ситуациях, где риск особенно высок (например, когда от результатов инвестиционного проекта зависит само существование предприятия).
Для применения минимаксного критерия построим "матрицу сожалений". В клетках этой матрицы показана величина сожаления- разность между фактическим и наилучшим результатами, которого могло бы добиться предприятие в данном состоянии природы. Сожаление показывает, что теряет предприятие в результате принятия неверного решения.
Таблица 2.15
Пример построения "матрицы сожалений" для минимаксного критерия
| Стратегия | Состояние природы | ||
| Отсутствие спроса | Средний спрос | Высокий спрос | |
| Построить линию малой мощности | (- 100)-(-100)=0 | 200-150=50 | 300-150=150 |
| Построить линию большой мощности | (-100)-(-200)=100 | 200-200=0 | 300-300=0 |
| Оптимальная стратегия для данного состояния природы | Построить линию малой мощности | Построить линию большой мощности | Построить линию большой мощности |
Минимаксное решение соответствует стратегии, при которой максимальное сожаление минимально. В нашем случае для линии малой мощности максимальное сожаление составляет 150 (в ситуации высокого спроса), а для линии большой мощности- 100 (при отсутствии спроса). Поскольку 100<150, минимаксное решение- построить линию большой мощности. Минимаксный критерий ориентируется не столько на фактические, сколько на возможные потери или упущенную выгоду.
Критерий Гурвица заключается в том, что минимальному и максимальному результатам каждой стратегии присваивается "вес". Оценка результата каждоq стратегии равна сумме максимального и минимального результатов, умноженных на соответствующий вес.
Пусть вес минимального и максимального результатов равен 0,5, вес максимального — также 0,5. Тогда расчет для каждой стратегии будет следующим:
линия малой мощности: 0,5 * (-100) + 0,5 * 150 = -50 + 75 = 25;
линия большой мощности: 0,5 * (-200) + 0,5 * 300 = -100 + 150 = 50.
Критерий Гурвица свидетельствует в пользу строительства линии большой мощности (поскольку 50>25). Достоинство и одновременно недостаток критерия Гурвица- необходимость присваивания весов возможным исходам: это позволяет учесть специфику ситуации, однако в присваивании весов всегда присутствует некоторая субъективность.
Вследствие того, что в реальных ситуациях часто отсутствует информация о вероятностях исходов, использование представленных выше методов в проектировании инвестиционных проектов вполне оправдано. Но выбор конкретного критерия зависит от специфики ситуаций и от индивидуальных предпочтений аналитика.
4. Анализ опционных методов. Опционные критерии оценки инвестиционных проектов основаны на предположении о том, что любой инвестиционный проект можно уподобить опциону. 0пцион- это ценная бумага, дающая владельцу право на покупку или продажу акции в некоторый будущий момент времени, но по заранее известной цене. Заплатив за опцион сейчас, инвестор покупает право на свободу выбора в будущем: он может либо воспользбваться этим выбором, либо нет. Стоимость опциона всегда неотрицательна (она положительна, если есть ненулевая вероятность получения выгоды от обещанной возможности, и равна нулю, если пользоваться этой возможностью невыгодно).
Обычная биномиальная модель оценки опционов выглядит следующим образом.
Пусть г- ставка процента, под которую можно привлечь или вложить капитал на один период, К - цена исполнения опциона покупателя, С- стоимость опциона покупателя в момент времени 0, 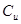 ,
, 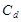 - стоимость опциона к концу срока, если цена акции в этот момент достигнет соответственно u*S и d*S.
- стоимость опциона к концу срока, если цена акции в этот момент достигнет соответственно u*S и d*S.
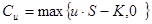 ,
,
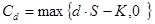
Доходы от опциона покупателя можно точно промоделировать доходами от соответствующим образом выбранного портфеля акций в количестве А и облигаций в количестве В. Такой портфель называется хеджированным портфелем. Так как опцион покупателя полностью эквивалентен портфелю, стоимости опциона и портфеля должны бьггь одинаковы.
Если наступит состояние и, то
А * u * S + r * B = 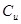
Если же наступит состояние d, то
А * u * S + r * B = 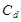
Решая полученную систему уравнений относительно A и В, получаем
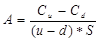 ,
,
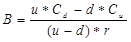
Так как доход от хеджированного портфеля равен доходу от опциона, стоимости их тоже должны быть равны:
С=А*S+B.
Достоинство метода- нет необходимости знать вероятности u и d.
Предлагается следующий теоретический подход к использованию опционных методов в анализе инвестиционных проектов: в качестве u*S и d*S можно взять денежные потоки от проекта в различных ситуациях (не обязательно знать вероятности этих ситуаций) и в качестве NPV использовать стоимость опциона. Основная трудность в том, что не во всех случаях можно подобрать адекватный промышленному проекту хеджированный портфель.
Применение опционных методов в анализе инвестиционных проектов представляется весьма перспективным, поскольку данные методы позволяют оценивать в денежном выражении имеющиеся у предприятия возможности и стоящие перед ним опасности.
Дата: 2019-07-30, просмотров: 333.