Когда речь идет о пространственной оптимизации, имеется в виду следующее:
- общая сумма финансовых ресурсов на конкретный период (допустим, год) ограничена сверху;
- имеется несколько взаимно независимых инвестиционных проектов с суммарным объемом требуемых инвестиций, превышающим имеющиеся у предприятия ресурсы;
- требуется составить инвестиционный портфель, максимизипующий суммарный возможный прирост капитала.
В зависимости от того, поддаются дроблению рассматриваемые проекты или нет, возможны различные способы решения данной задачи. Рассмотрим их последовательно.
Рассматриваемые проекты поддаются дроблению .
Имеется в виду, что можно реализовывать не только целиком каждый из анализируемых проектов, но и любую его часть; при этом берется к рассмотрению соответствующая доля инвестиций и денежных поступлений. Последовательность действий в этом случае такова:
для каждого проекта рассчитывается индекс рентабельности PI;
проекты упорядочиваются по убыванию показателя PI;
в инвестиционный портфель включаются первые проектs, которые в сумме в полном объеме могут быть профинансированы предприятием;
очередной проект берется не в полном объеме, а лишь в той части, в которой он может быть профинансирован (остаточный принцип).
Можно проверить, что любая другая комбинация ухудшает результаты- уменьшает суммарный NPV.
Рассматриваемые проекты не поддаются дроблению .
В этом случае оптимальную комбинацию находят последовательным просмотром всех возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной.
2 . Временная оптимизация.
Когда речь идет о временной оптимизации, имеется в виду следующее:
- общая сумма финансовых ресурсов, доступных для финансирования в планируемом году, ограничена сверху;
- имеется несколько доступных независимых инвестиционных проектов, которые ввиду ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в следующем за планируемым годом оставшиеся проекты либо их части могут быть реализованы;
- требуется оптимально распределить проекты по двум годам.
В основу методики составления оптимального портфеля заложена следующая идея: по каждому проекту рассчитывается специальный индекс, характеризующий относительную потерю NPV в случае, если проект будет отсрочен к исполнению на год. Проекты с минимальными значениями индекса могут быть отложены на следующий год.
Например, есть следующие проекты:
Таблица 2.6
| Проект | Инвестиции | NPV |
| А | 30 | 2,51 |
| Б | 20 | 2,68 |
| В | 40 | 4,82 |
| Г | 15 | 1,37 |
Задача: составить оптимальный инвестиционный портфель на два года в случае, если объем ннвестиций на планируемый год ограничен суммой в 70.
1. Рассчитаем потери в NPV в случае, если каждый из анализируемых проектов будет отсрочен к исполнению на год:
Таблица 2.7
| Проект | NPV в году 1 | Дисконтирующий множитель при r=10% | NPV в году 0 | Потеря в NPV | Величина отложенной на год инвестиции | Индекс возможных потерь |
| А | 2,51 | 0,9091 | 2,28 | 0,23 | 30 | 0,0077 |
| Б | 2,68 | 0,9091 | 2,44 | 0,24 | 20 | 0,0120 |
| В | 4,82 | 0,9091 | 4,38 | 0,44 | 40 | 0,0110 |
| Г | 1,37 | 0,9091 | 1,25 | 0,12 | 15 | 0,0080 |
Индекс возможных потерь имеет следующую интерпретацию: он показывает, чему равна величина относительных потерь в случае откладывания проекта к исполнению на год. Из расчета видно, что наименьшие потери будут в том случае, когда отложен к исполнению проект А, затем последовательно проекты Г, В, Б.
Таким образом, инвестиционный портфель первого года должен включить проекты Б и В в полном объеме, а также часть проекта Г; оставшуюся часть проекта Г и проект А следует включить в портфель второго года:
Таблица 2.8
| Проект | Инвестиции | Часть инвестиций, включенная в портфель, в % | NPV |
| А) инвестиции в году 0: Б В Г Всего | 20 40 10 70 | 100 100 67 | 2,68 4,82 0,92* 8,42 |
| А) инвестиции в году 1: Г А Всего | 5 30 35 | 33 100 | 0,41** 2,28 2,69 |
Пояснения к расчетам: * 0,92 = 1,37*0,67;
** 0,41 = 1,25*0,33.
Суммарный NPV при таком формировании портфелей за два года составит 11,11 (8,42 + 2,69), а общие потери будут равны 0,27 (2,51+2,68+4,82+1,37—11,11) и будут минимальны по сравнению с другими вариантами формирования портфелей.
Мы рассмотрели наиболее распространенные методы оценки инвестиционных проектов; существуют и более сложные методы и критерии.
Таким образом, можно предложить следующий несложный алгоритм формирования инвестиционного портфеля предприятия в условиях ограниченности финансовых средств:
1. Утверждаются все неизбежные инвестиционные проекты (приносящие и не приносящие денежный доход)
2. Прогнозируется прибыль от неизбежных (уже принятых) инвестиционных проектов.
3. Рассчитывается капитал, остающийся после шагов по п. п. 1, 2 – это сумма, которую предприятие может вложить в приносящие прибыль инвестиционные проекты.
4. Определяются минимально приемлимая доходность оставшейся части инвестиционного портфеля и максимально приемлимый риск.
5. Анализируются имеющиеся альтернативы (прибыльные инвестиционные проекты)
6. Отбор ведется по уже рассмотренным критериям.
Двойной бюджет
Для защиты стратегической работы некоторые фирмы разделяют свой бюджет на два: текущий и стратегический. Текущий бюджет обеспечивает непрерывное получение прибыли от использования действующих мощностей фирмы, капиталовложения в увеличение мощностей, капиталовложения ради увеличения прибыли с помощью снижения себестоимости. Стратегический бюджет предусматривает капиталовложения в повышение конкурентоспособности предприятия в стратегических зонах хозяйствования, освоение новых рынков, освоение новых направлений деятельности и прекращение капиталовложений в неприбыльные направления деятельности.
Двойной бюджет дает следующие преимущества:
• средства вьщеляются целевым порядком для стратегической деятельности, что защищает их от "посягательств" со стороны текущей деятельности;
• деление бюджета на два помогает сбалансировать капиталовложения и доходы в коротком и долгом периодах;
• критерии оценки проектов зависят от цели осуществления проекта (краткосрочный или долгосрочный эффект);
• двойной бюджет помогает осуществлять оперативный и стратегический контроллинг.
Соответственно и составление инвестиционного плана также разбивается на две части:
• стратегический инвестиционный план разрабатывается на длительную перспективу, на основе анализа внешней и внутренней сред, балансирования жизненных циклов различных стратегических зон хозяйствования, анализа синергизма, стратегической гибкости и др. (при этом финансовые показатели играют подчиненную роль);
• при составлении текущего бюджета ориентируются на показатели рентабельности с учетом ограничений на ликвидность, структуру капитала и т. п. При этом обычно для дисконтирования денежных потоков по проектам различных типов применяются различные ставки дисконтирования. Недостаток двойного бюджета в том, что он создает поле для всевозможных манипуляций (часто трудно бывает с полной определенностью отнести инвестиционный проект к одной из двух категорий).
Инвестиционные решения с дополнительной информацией (вариант пробных инвестиций )
Здесь будет рассмотрен вариант определения NPV для специфических инвестиционных проектов.
Иногда перед принятием инвестиционного решения можно получить дополнительную информацию. Это связано с тем, что в условиях неопределенности возникает возможность того, что считавшиеся приемлимыми инвестиции окажутся на практике невыгодными и наоборот, если будет получена дополнительная информация.
В модели сравниваются затраты связанные с получением информации и выгоды от нее. В рамках этой задачи решаются следующие проблемы:
1. Стоит ли собирать необходимую информацию
2. Использование дополнительной и ранее имеющейся информации для принятия решения.
3. Интерпретация результатов проверки.
Необходимость такого анализа: если сам по себе единичный инвестиционный проект убыточен, но с учетом последующих инвестиций в контексте проекта он может оказаться выгодным. (например: мы планируем модернизировать оборудование на одном технологическом участке и NPV получился отрицательным, но есть вероятность, что в дальнейшем исход инвестиций в модернизацию аналогичного оборудования на других участках окажется выгодным, то есть используется вероятностный подход). Иначе говоря, чем более неопределенным является результат, тем выгоднее собрать дополнительную информацию (например, с помощью экспериментальных инвестиций).
Инвестиционные решения с дополнительной информацией с полной дополнительной информацией.
Смысл понятия полная дополнительная информация: это значит, что осуществление пробного (единичного) инвестиционного проекта однозначно определяет что будет, если осуществляться все прочие аналогичные проекты. Идея метода- осуществление пробного инвестпроекта с отрицательным NPV оправдано, если позволит получить ценную информацию (если ожидаемая стоимость полной информации будет больше ожидаемых затрат на единичные инвестиции).
NPV в данной модели может быть потеряна из-за того, что инвестиции не осуществлялись. Пусть Vo- NPV пробного проекта (случайная величина), Vo ср- ее матожидание, Vb- точка безубыточности (Vb соответствует случаю Vo=0), С- угол наклона кривой NPV для всех, включая последующие инвестиции.
Если ожидаемое Vo<0 и если Vo подчиняется некоторому закону распределения вероятности и есть вероятность, что Vo>Vb, то требуется дальнейший анализ. Если в дальнейшем окажется, что при Vo ср<0 Vo>0, то ожидаемая прибыль будет равна : 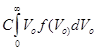
Где f(Vo)- функция плотности вероятности для Vo.
Таким образом, мы можем уменьшать потенциальные потери от неопределенности, осуществляя пробные инвестиции с NPV<0. Даже когда NPV эксперементальных инвестиций больше нуля, то все равно желательно провести пробные инвестиции.
Приведем простой пример.
Таблица 2.9
| Событие | Вероятность события | NPV | Ожидаемая текущая стоимость |
| А | 0,3 | 400 | 120 |
| Б | 0,7 | -500 | -350 |
| Итого | NPV=-70 |
Пусть С=10.
Если осуществив все инвестиции сразу, есть вероятность 0,3 получить NPV=4000, а есть вероятность 0,7 потерять NPV=–5 000, матожидание (4000*0,3-500*0,7=-2300)<0 и инвестиции будут невыгодными. Но можно уменьшить потери от неопределенности, сделав пробные инвестиции и если произойдет событие А, получить прибыль (в условиях полноты дополнительной информации). Ожидаемая стоимость пути А для С=10 равна 0,3*4000=1200. Ожидаемая стоимость пути B равна (-500)*0,7=-350. Ожидаемая NPV пробных инвестиций равна: 1200-350=850>0, что говорит о желательности пробных инвестиций в надежде, что произойдет событие А.
Анализ пробных инвестиций при нормальных априорных распределениях вероятностей при полной дополнительной информации.
Исходная посылка- вероятности исходов распределены нормально.
Пусть матожидание равно Vo ср, среднеквадратическое отклонение равно d о, задано С.
Так как NPV<0, проект можно было бы однозначно отвергнуть, лишь если бы дисперсия была равна нулю. Если есть вероятность Vo>0, то нужно посчитать ожидаемую текущую стоимость всех инвестиций С (обозначим эту стоимость EVPI).
EVPI=cdoL(D), где
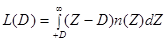
n(Z)- нормальная функция плотности вероятности для нормированной случайной величины,
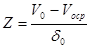
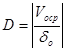
Из таблицы интегральной функции потерь для нормального распределения вероятностей можно найти L(D) , а затем и EVPI=ожидаемая прибыль.
Пусть L(D*)=D+L(D) , тогда ожидаемые затраты на пробные инвестиции равны:
E(Lo)= d оL(D*).
Теперь если EVPI (ожидаемая стоимость полной информации)>Е(Lo), то пробные инвестиции с NPV пробных инвестиций<0 целесообразны.
Зная NPV пробных инвестиций, можно определить количество пробных инвестиций для того, чтобы ожидаемая стоимость полной информации пробных инвестиций была больше ожидаемых затрат на них: k=E(Lo)/EVPI` , где EVPI` равно EVPI при С=1.
Дата: 2019-07-30, просмотров: 345.