Исходные данные: ежедневные суммарные зачисления и списания со счетов юридических лиц за апрель месяц.
| число месяца | день недели | сумма зачислений (тыс. руб) | сумма списаний (тыс. руб) |
| 1 | ср | 47 | 46 |
| 2 | чт | 44 | 54 |
| 3 | пт | 31 | 42 |
| 4 | сб | 28 | 28 |
| 5 | вс | ||
| 6 | пн | 42 | 57 |
| 7 | вт | 48 | 26 |
| 8 | ср | 39 | 48 |
| 9 | чт | 40 | 45 |
| 10 | пт | 38 | 32 |
| 11 | сб | 15 | 29 |
| 12 | вс | ||
| 13 | пн | 45 | 52 |
| 14 | вт | 53 | 33 |
| 15 | ср | 41 | 50 |
| 16 | чт | 27 | 22 |
| 17 | пт | 56 | 36 |
| 18 | сб | 25 | 14 |
| 19 | вс | ||
| 20 | пн | 51 | 59 |
| 21 | вт | 32 | 49 |
| 22 | ср | 49 | 30 |
| 23 | чт | 21 | 31 |
| 24 | пт | 35 | 43 |
| 25 | сб | 13 | 16 |
| 26 | вс | ||
| 27 | пн | 58 | 40 |
| 28 | вт | 59 | 41 |
| 29 | ср | 29 | 39 |
| 30 | чт | 30 | 61 |
Построим двумерную корреляционную таблицу:
|
| i | 1 | 2 | 3 | 4 | 5 | 6 | ||
| j | Y \ X | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |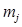 
| |
| 1 | 12 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 2 | 20 | 1 | 0 | 1 | 0 | 0 | 0 | 2 | |
| 3 | 28 | 1 | 1 | 1 | 0 | 2 | 0 | 5 | |
| 4 | 36 | 0 | 0 | 1 | 1 | 1 | 1 | 4 | |
| 5 | 44 | 0 | 0 | 2 | 1 | 1 | 2 | 6 | |
| 6 | 52 | 0 | 0 | 1 | 3 | 1 | 0 | 5 | |
| 7 | 60 | 0 | 0 | 1 | 1 | 1 | 0 | 3 | |
| n i | 2 | 2 | 7 | 6 | 6 | 3 | 26 | ||
| | 24 | 20 | 40 | 49 | 41 | 41 | |||
| | 0 | 0 | 0,57 | 0,33 | 0,33 | 0,33 | |||
Общая средняя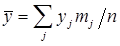 
, 
.
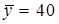Общая дисперсия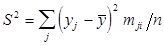 
, 
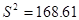
Средняя из групповых дисперсий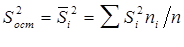 
, 
.
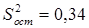Дисперсия групповых средних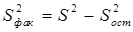 
, 
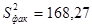
Выборочная средняя и дисперсия компоненты Х :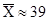 
и 
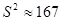(расчеты см. выше).
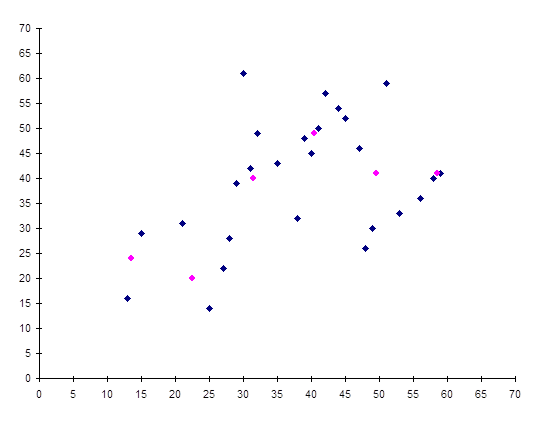
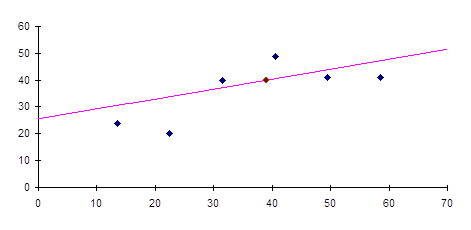
График поля корреляции и линия групповых средних компоненты Y.
| Y\X=12 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 0 | 1 | 0 | 0 | 0 | 0 |
M[Y/X=12] = 22,5
D[Y/X=12] = 0
| Y\X=20 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 1/2 | 0 | 1/2 | 0 | 0 | 0 |
M[Y/X=20] = 22,5
D[Y/X=20] = 81
| Y\X=28 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 1/5 | 1/5 | 1/5 | 0 | 2/5 | 0 |
M[Y/X=28] = 33,3
D[Y/X=28] = 207,36
| Y\X=36 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 0 | 0 | 1/4 | 1/4 | 1/4 | 1/4 |
M[Y/X=36] = 45
D[Y/X=36] = 101,25
| Y\X=44 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 0 | 0 | 2/6 | 1/6 | 1/6 | 2/6 |
M[Y/X=44] = 45
D[Y/X=44] = 128,25
| Y\X=52 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 0 | 0 | 1/5 | 3/5 | 1/5 | 0 |
M[Y/X=52] = 40,5
D[Y/X=52] =32,4
| Y\X=60 | 13,5 | 22,5 | 31,5 | 40,5 | 49,5 | 58,5 |
| 0 | 0 | 1/3 | 1/3 | 1/3 | 0 |
M[Y/X=60] = 40,5
D[Y/X=60] = 54
D[Y, ост] = 121,25
Коэффициент детерминации К = 1 - 121,25/169 = 0,28
Корреляционное отношение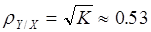 
(близость корреляционного отношения к единице указывает на то, что зависимость Y от Х близка к функциональной).
Корреляционный момент
, 
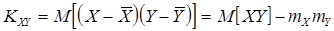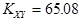
Коэффициент корреляции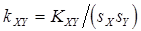 
, 
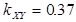. Показывает степень линейной зависимости между случайными величинами.
Выборочный коэффициент детерминации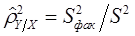 
, равен 1,008.
Выборочное корреляционное отношение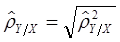 
, равен 1,004.
Отношение коэффициента детерминации и коэффициента корреляции равно 0,76.
Уравнение регрессии y=0.37x+25.57. Прямая регрессии обязательно проходит через точку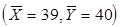 
.
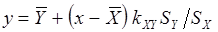
Теперь оценим, на сколько процентов (по отношению к размеру среднего ежедневного зачисления) изменится ожидаемое значение ежедневного списания при увеличении на 1% (по отношению к размеру ежедневного списания) ежедневного зачисления.
y=0.37x+25.57
(0,37*40,4+25,57)/(0,37*40+25,57)=1,004
Значит, при увеличении ежедневного зачисления на 1% ожидаемое значение ежедневного списания увеличится на 0,4%.
Дата: 2019-07-30, просмотров: 257.
