Риск как среднее квадратическое отклонение — еще одно понимание риска. Рассмотрим какую-нибудь операцию, доход которой есть случайная величина Q. Как уже указывалось, средний ожидаемый доход — это математическое ожидание случайно величины Q. А вот среднее квадратическое отклонение _Q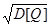=  —  это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Напомним, что D[Q] = M[(Q - m_Q)²].

Найдем риски в их новом определении r_i доходов Q_i.

             10    8    2    4

Q =        -6 -2 10   -6

             10     2   4 16

             -6  15 -4     3

p_j = ( 1/4 1/4 1/3 1/6 )

         10   8   2   4

Q₁ :

        1/4 1/4 1/3 1/6

          -6  -2 10  -6

Q₂ :

        1/4 1/4 1/3 1/6

         10   2   4 16

Q₃ :

        1/4 1/4 1/3 1/6

         -6  15 -4   3

Q₄ :

        1/4 1/4 1/3 1/6

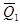 = 10/4+8/4+2/3+4/6 = 70/12 5.83

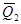 = -6/6-2/4+10/3-6/6 = 4/12 0.33

 = 10/4+2/4+4/3+16/6 = 84/12 = 7

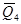 = -6/6+15/4-4/3+3/6 = 17/12  1.42

D₁ = 2384/144  16.56 r₁ 4.7

D₂ = 443/9  49.22 r₂ 7.2

D₃ = 25 r₃ = 5

D₄ = 10091/144  70.08 r₄ 8.37

Нанесем средние ожидаемые доходы и риски на плоскость — доход 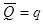 откладываем по вертикали, а риски — по горизонтали.

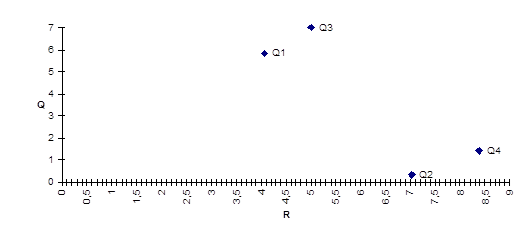
Получили четыре точки. Чем выше точка (q, r), тем более доходная операция, чем точка правее — тем более она рисковая. Значит, нужно выбирать точку левее и выше. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. В данном примере точка Q₃  доминирует точки Q₂ и Q₄, точка Q₁ доминирует точки Q₂ и Q₄. Точки Q₁ и Q₃ несравнимы — доходность 3-ей больше, но и риск ее тоже больше. Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбирать из операций, оптимальный по Парето.

Предположим, что все операции независимы друг от друга, тогда можно выяснить, нет операции, являющейся линейной комбинацией основных операций, более хорошей, чем имеющиеся.

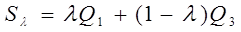
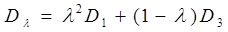
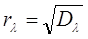
Теперь найдем 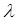, при которой риск будет минимальным. Т.к. 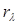стремится к минимуму, то  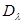также стремиться к минимуму.

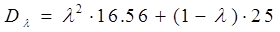
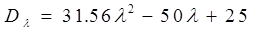
График данной функции представляет собой параболу, ветви направлены вверх, значит, минимальное значение данной функции будет в точке перегиба — операция, являющаяся линейной комбинацией основных операций, будет иметь минимальный риск при 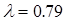. Этот риск будет равен 3.38, а доход соответственно 6,08. Полученная точка Q’(6.08, 3.38) доминирует точку Q₁(5.83,4.07).

Для нахождения лучших операций иногда применяют подходящую взвешивающую формулу, которая для пар (q, r) дает одно число, по которому и определяют лучшую операцию.

Для анализа ситуаций применим взвешивающую формулу E(Q, r) = 4Q - r. Данная формула говорит, что доход ценится в четыре раза больше, чем риск, т.е. увеличение риска на 4 компенсируется увеличением дохода на единицу.

Тогда для 1-ой операции Е = 19.25, для 3-ей операции Е = 23. При сравнении результатов анализа видно, что при данном отношении к рискованности операций лучшей является 3-я операция.

Часть III . Анализ денежных потоков.