Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Предположим, что в рассматриваемой схеме известны вероятности p_j того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.

Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения,   

является случайной величиной Q_i с рядом распределения                  

qi1	. . .	qin
p1		pn

Математическое ожидание MQ_iи есть средний ожидаемый доход, обозначаемый также Q_i. Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.

В приведенном примере вероятности такие (1/2, 1/4, 1/5, 1/20).          

                        0 6 5  2

       Q =     6 2 8 22

                       9 4 3 32

                     -6 -4 -12 10 

 

           р_j = ( 1/2 1/4 1/5 1/20 ) 

          0    6   5   2

Q₁ :

        1/2 1/4 1/5 1/20

          6   2   8  22

Q₂ :

        1/2 1/4 1/5 1/20

          9   4   3  32

Q₃ :

        1/2 1/4 1/5 1/20

 

         -6   -4 -12 10

Q₄ :

        1/2 1/4 1/5 1/20

Q₁ = 6/4 + 5/5 + 2/20 = 1,5 + 1 +0,1 = 2,6

Q₂ = 6/2 + 2/4 + 8/5 + 22/20 = (30+5+16+11)/10 = 62/10 = 6,2

Q₃ = 9/2 + 4/4 + 3/5 + 32/20 = (45+10+6+16)/10 = 77/10 = 7,7

Q₄ = - 6/2 - 4/4 - 12/5 + 10/20 = (-30-10-24+5)/10 = - 59/10 = -5,9

 

Максимальный средний ожидаемый доход равен 7.7, что соответствует 3-му решению.

Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения является случайной величиной R_i с рядом распределения

ri1	. . .	rin
p1		pn

     

Математическое ожидание M[R_i] и есть средний ожидаемый риск, обозначаемый также R_i. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск. Вычислим средние ожидаемые риски.

                       9 0 3 30

        R =   3 4 0 10

                      0 2 5 0

                    15 10 20 22

р_j = ( 1/2 1/4 1/5 1/20 ) 

 

          9   0   3  30

R₁ :

        1/2 1/4 1/5 1/20

 

          3   4   0  10      

R₂ :

        1/2 1/4 1/5 1/20

          0   2   5   0

R₃ :

        1/2 1/4 1/5 1/20

         15 10 20 22

R₄ :

           1/2 1/4 1/5 1/20

R₁ = 9/2 + 3/5 + 30/20 = (45+6+15)/10 = 66/10 = 6.6

R₂ = 3/2 + 4/4 +10/20 = 1.5 + 1 +0.5 = 3

R₃ = 2/4 + 5/5 = 15/10 = 1.5

R₄ = 15/2 + 10/4 + 20/5 + 22/20 = (150+50+80+22)/20 = 302/20 = 15.1

 

Минимальный средний ожидаемый риск равен 1.5, что соответствует 3-му решению.

Иногда в условиях полной неопределенности применяется следующее правило.

Правило Лапласа равновозможности, когда все вероятности p считаются равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.

Правило максимизации среднего ожидаемого дохода.

Q =	0 6 5  2 6 2 8 22 9 4 3 32 6 -4 -12 10

 

р_j = ( 1/4 1/4 1/4 1/4 ) 

          0    6   5   2

Q₁ :

        1/4 1/4 1/4  1/4

 

          6   2   8  22

Q₂ :

        1/4 1/4 1/4   1/4

 

 

          9   4   3  32

Q₃ :

        1/4 1/4 1/4  1/4

 

         -6   -4 -12 10

Q₄ :

        1/4 1/4 1/4 1/4

 

Q₁ = (6+5+2)/4 = 13/4 = 3,25

Q₂ = (6+2+8+22)/4 = 38/4 = 9,5

Q₃ = (9+4+3+32)/4 = 48/4 =12

Q₄ = (-6-4-12+10)/4 = -12/4 = -3

 

Максимальный средний ожидаемый доход равен 12, что соответствует 3-му решению.

Правило минимизации среднего ожидаемого риска.

                      9 0 3 30

        R =   3 4 0 10

                      0 2 5 0

                    15 10 20 22

р_j = ( 1/2 1/4 1/5 1/20 ) 

          9   0   3  30

R₁ :

        1/4 1/4 1/4  1/4

          3   4   0  10      

R₂ :

        1/4 1/4 1/4  1/4

 

          0   2   5   0

R₃ :

        1/4 1/4 1/4     1/4

 

         15 10 20 22

R₄ :

        1/4 1/4 1/4  1/4

R₁ = (9+3+30)/4 = 42/4 = 10,5

R₂ = (3+4+10)/4 = 17/4 = 4,25

R₃ = (2+5)/4 = 7/4 = 1,75

R₄ = (15+10+20+22)/4 = 67/4 = 16,75

 

Минимальный средний ожидаемый риск равен 1.75, что соответствует 3-му решению.

При данных вероятностях состояний теперь требуется проанализировать семейство из 4-х операций: каждая операция имеет две характеристики — средний ожидаемый доход и средний ожидаемый риск. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. Точка, не доминируемая никакой другой, называется оптимальной по Парето.

Нанесем для каждой операции эти характеристики на плоскую систему координат для выявления операции, оптимальной по Парето, доход по вертикали и риск по горизонтали.

 

q 2.6 6.2 7.7 -5.9

r 6.6 3 1.5 15.1

 

Получим четыре точки. Чем выше точка (q, r), тем доходнее операция, чем правее точка, тем более она рисковая. Значит, нужно выбирать выше и левее. Это точка Q₃ (7.7, 1.5). Она является оптимальной по Парето, т.к. доминирует остальные точки.

Затем найдем выпуклую оболочку множества полученных точек и дадим интерпретацию точек полученной выпуклой оболочки.

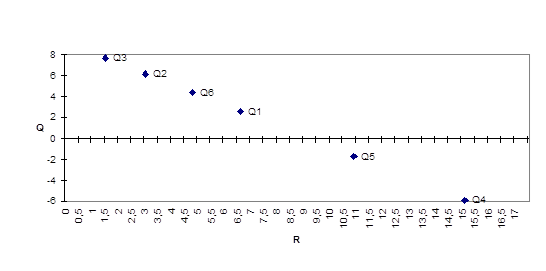
Точка Q₅ находится на равных расстояниях от точек Q₁ и Q₄, и соответственно имеет координаты (10.9, -1.7). Аналогично, точка Q₆  расположена между точками Q₁ и Q₂ и имеет координаты (4.8, 4.4).