Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ΔG⁰_T=ΔH⁰_T – TΔS⁰_T

При стандартной температуре

ΔG⁰₂₉₈=ΔH ⁰₂₉₈– TΔS⁰₂₉₈

ΔG⁰₂₉₈ – стандартная энергия Гиббса, изменение энергии Гиббса при образовании 1 моль вещества из простых веществ в стандартных условиях, (кДж/моль).

Стандартную энергию Гиббса реакции рассчитывают по первому следствию из закона Гесса.

∆_rG ⁰₂₉₈= ∑(n _j Δ_fG⁰₂₉₈) _прод. -∑ (n _i Δ_fG⁰₂₉₈)_исход.

ΔS⁰₂₉₈ - стандартная энтропия 1 моль вещества в стандартном условиях, (Дж/К*моль). Энтропию можно характеризовать как меру беспорядка (неупорядоченности) системы. Эта величина характеризует изменение температуры в системе.

Поскольку энтропия – функция состояния системы, ее изменение (ΔS) в процессе химической реакции можно подсчитать, используя следствие из закона Гесса.

Δ_rS⁰₂₉₈ =∑ (n _j Δ_fS⁰₂₉₈) _прод. –∑(n _i Δ_fS⁰₂₉₈)_исход

где, n _j и n _i – количество вещества продуктов реакции и исходных веществ соответственно (численно равно коэффициенту в уравнении реакции), (моль).

Δ_rS⁰₂₉₈ =∑ (n _i Δ_fS⁰₂₉₈) _исход –∑(n _j Δ_fS⁰₂₉₈)_прод

где, n _i и n _j - количество вещества исходных веществ и продуктов реакции соответственно (численно равно коэффициенту в уравнении реакции), (моль).

Δ_rS⁰₂₉₈ – стандартная энтропия реакции, (Дж/К).

Δ_fS⁰₂₉₈ – стандартная энтропия образования химического вещества, (Дж/К*моль).

Знак « - » перед членом TΔS⁰₂₉₈ (энтропийным членом) ставится, для того чтобы при ΔH=0 сделать ∆G отрицательной величиной ΔG<0 – условие самопроизвольного протекания реакции.

Если пренебречь изменением ΔS⁰ и ΔН⁰ с увеличением температуры, то можно определить Т_равн, т.е. температуру, при которой устанавливается химическое равновесие химической реакции для стандартного состояния реагентов, т.е. из условия равновесия реакции ΔG=0 имеем 0=Δ_rH ⁰₂₉₈– TΔ_rS ⁰_298, отсюда

Следует знать:

Если ΔS=0 (ΔS>0), ΔH<0(ΔH=0) то ΔG <0 – реакция протекает самопроизвольно, процесс протекает в прямом направлении (энергетически выгоден).

Если ΔS=0(ΔS<0), ΔH>0 (ΔH=0) то ΔG>0 – протекание реакции невозможна, возможна только в обратном направлении (энергетически невыгоден).

Если ΔS=0, ΔH=0 ΔG=0 – система находится в состоянии равновесия.

Примеры решения задач

1. Вычислить тепловой эффект реакции получения гидроксида кальция

СаО_(т) + Н₂О_(ж) = Са(ОН)_2(т), если теплота образование СаО_(т) равна +635701,5Дж/моль, теплота образования Н₂О_(ж) +285835,5 Дж/моль и теплота образования Са(ОН)₂ +986823 Дж/моль.

Решение:

Тепловой эффект реакции

 СаО _(т) + Н₂О _(ж) = Са(ОН)_2(т) по первому следствию закона Гесса, будет равен теплоте образования Са(ОН)_2(т) минус теплота образования Н₂О_(ж) и теплота образования (СаО_(т)):

Δ_rН⁰₂₉₈ =∑(n_j •Δ_fН⁰₂₉₈)_прод - ∑(n_i• Δ_fН⁰₂₉₈)_исх.

Δ_rН⁰₂₉₈=1 моль•Δ_fН⁰₂₉₈(Са(ОН)_2(т)) - (1 моль Δ_fН⁰₂₉₈(СаО_(т)) +

+1 моль• Δ_fН⁰₂₉₈(Н₂О _(ж)))=1 моль*986823 Дж/моль - (1 моль* 635701,5 Дж/моль +

+ 1 моль*285835,5 Дж/моль)= 65 286 Дж.

Ответ: 65286 Дж.

2. Вычислите изменения энергии Гиббса в реакции димеризации диоксида азота при стандартной температуре, при 0 и 100ºС. Сделать вывод о направлении процесса.

Решение:

При стандартной температуре 298 К изменение энтальпии в реакции

2NO_{2 (г)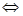} N₂O_4(г) равно (первое следствие закона Гесса)

Δ_rН⁰₂₉₈ =∑(n_j •Δ_fН⁰₂₉₈)_прод - ∑(n_i• Δ_fН⁰₂₉₈)_исх.

Δ _rН⁰₂₉₈ =1 моль* 9660 Дж/моль – 2 моль*33800 Дж/ моль = - 57940 Дж

Изменение температуры равно

Δ_rS⁰₂₉₈ =∑ (nΔ_fS⁰₂₉₈) _прод. –∑(nΔ_fS⁰₂₉₈)_исход = 1 моль*304 Дж/моль*К -

–2 моль*234 Дж/моль*К = - 164 Дж/К

Зависимость энергии Гиббса реакции от температуры описывается уравнением

ΔG⁰_T =ΔH⁰_T – TΔS⁰_T

При стандартной температуре

Δ_rG⁰₂₉₈=ΔH ⁰₂₉₈– TΔS⁰₂₉₈ = - 57940 Дж – (298 К*(-164 Дж/К)) = -9068 Дж/моль

Отрицательное значение энергии Гиббса реакции говорит о том, что смещении равновесия вправо (самопроизвольный процесс), т.е. в сторону образования диоксида азота.

При 0ºС (273К)

Δ_rG⁰₂₇₃ = -57940 Дж + 273К* 164 Дж/К = -13168 Дж/моль

Более высокое отрицательное значение ΔG₂₇₃ по сравнению с ΔG⁰₂₉₈ свидетельствует о том, что при 273 К равновесие еще больше смещено в сторону прямой реакции.

При 100ºС (373 К)

Δ_rG₃₇₃ = -57940 Дж + 373К*164 Дж/К = 3232 Дж/моль.

Положительная величина ΔG₃₇₃ указывает на изменение направления реакции: равновесие смещено влево, т.е. в сторону распада димера N₂O₄ (реакция невозможна). Ответ: при 0ºС (273 К) Δ_rG₂₇₃= -13168 Дж/моль, реакция протекает самопроизвольно; при 100ºС (373 К) Δ_rG₃₇₃= 3232 Дж/моль, реакция невозможна.

3. Составьте термохимическое уравнение горения метана СН₄ и рассчитайте объем воздуха, необходимый для сжигания 1моль метана, если известно, что при сгорании 5,6 л метана выделяется 220 кДж теплоты, содержание кислорода в воздухе равно 20%.

Решение:

СН₄ + 2О₂ = СО₂ + 2Н₂О, ∆Н<0

Находим количество вещества метана объемом 5,6 л

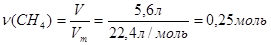
Если при сгорании СН₄ количеством вещества 0,25 моль выделяется 220 кДж теплоты, то при сгорании СН₄ количеством вещества 1 моль выделяется 880 кДж теплоты.

Термохимическое уравнение:

СН₄ +2О₂ = СО₂+ 2Н₂О+ 880 кДж

Из уравнения реакции видно, что на сгорание СН₄ количеством вещества 1моль расходуется О₂ количеством вещества 2 моль, на сгорание СН₄ количеством вещества 0,25 моль расходуется х моль О₂, откуда х = 0,5 моль.

Кислород количеством вещества 0,5 моль занимает объем 11,2 л.

В воздухе 20% кислорода, следовательно, объем воздуха будет равен

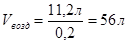
Ответ: 880 кДж, 56 л.

Задачи для самостоятельного решения

1. Рассчитайте, какая из ниже перечисленных реакций при стандартных условиях может идти самопроизвольно:

а) Fe_(к) + Al₂O_3(к) = Al_(к) + Fe₂O_3(к)

б) Al_(к) + Fe₂O_{3 (к)}= Fe_(к) + Al₂O_3(к)

в) CuSO_4(к) + 2NH₄OH_(ж) = Cu(OH)_2(к) + (NH₄)₂SO_4(к)

г) Al₂O_{3(корунд)} + 3SO₃ = Al₂(SO₄)_2(к)

2. При сварке трамвайных рельсов используют термитную смесь, которую готовят, смешивая порошки алюминия и оксида железа (III) в количественном отношении 2:1. Термохимическое уравнение горения термитной смеси следующее: 2Al + Fe₂O₃= Al₂O₃ + 2Fe + 829,62 кДж. Сколько теплоты выделится при образовании: 1) 4 моль железа; 2) 1 моль железа?

3. Рассчитайте, достаточно ли теплоты, выделяющейся при сгорании 200 кг каменного угля, содержащего 82% углерода, для полного разложения 162 кг карбоната кальция, если для разложения 1 моль СаСО₃ необходимо 180 кДж теплоты, а при сгорании 1 моль углерода, входящего в состав каменного угля, выделяется 402 кДж теплоты.

4. Процесс алюминотермии выражается химическим уравнением

8Al + 3 Fe₃O₄ = 4Al₂O₃ + 9Fe ΔH<0. Рассчитайте, сколько теплоты выделится при сгорании 1 кг термита.

5. Возможен ли обжиг колчедана массой 1т по следующему уравнению химической реакции 4FeS₂ + 11O₂ →2 Fe₂O₃ + 8SO₂ ∆H<0

6. Вычислите тепловой эффект образования NH₃ из простых веществ, при стандартном условии по тепловым эффектам реакции:

2H₂ + O₂ = 2H₂O_(ж) ΔН⁰₁ = -571, 68 кДж,

NH₃ + 3O₂ = 6H₂O_(ж) + 2N₂ ΔН⁰₂ = -1530,28 кДж.

7. Стандартный тепловой эффект реакции сгорания этана равен -1560 кДж. Рассчитайте стандартную теплоту образования этана, если известно, что

Δ_fН⁰₂₉₈ (H₂O)= -285,84 кДж/моль и Δ_fН⁰₂₉₈(СО₂) = -396,3 кДж/моль.

8. Вычислите тепловой эффект реакции восстановления оксида железа водородом, пользуясь следующими данными.

FeO + CO = Fe + CO₂ ΔН = -13,19 кДж

CO + 1/2O₂ = CO₂ ΔН = -283,2 кДж

2H₂ + 1/2O₂ = 2H₂O_(г) ΔН = -242 кДж

9. Протекание, какой из приведенных реакций восстановления оксида железа (III) наиболее вероятно при 298 К.

Fe₂O_3(k) + 3H_2(г) = 2Fe_(к) + 3H₂O_(к)

Fe₂O_3(k) + 3С_{(графит)} = 2Fe_(к) + 3СO_(к)

Fe₂O_3(k) + 3СО_(г) = 2Fe_(к) + 3СО_2(к)

10. В какой их перечисленных ниже реакций тепловой эффект ΔН⁰₂₉₈ будет стандартной теплотой SO_3(г)

а) S_(г) + 3/2 O₂ = SO_3(г)

а) S_(г) + 1/2 O₂ = SO_3(г)

а) S_(к) + 3/2 O₂ = SO_3(г)

 

3.1.2 Химическое равновесие

При протекании химической реакции через некоторое время устанавливается равновесное состояние (химическое равновесие). Слово «равновесие» означает состояние, в котором сбалансированы все противоположно направленные на систему воздействия. Тело, находящееся в состоянии устойчивого равновесия, обнаруживает способность возвращаться в это состояние после какого-либо возмущающего воздействия.

Примером тела, находящегося в состоянии устойчивого равновесия, может служить шарик, лежащий на дне ямки. Если его толкнуть в одну или другую сторону, он вскоре снова возвращается в состояние устойчивого равновесия. В отличие от этого шарик, лежащий на краю ямки, находится в состоянии неустойчивого равновесия — достаточно ничтожного толчка, чтобы он необратимо скатился в ямку.

Оба этих примера являются примерами статического равновесия. В химии, однако, приходится сталкиваться не столько со статическими равновесиями, столько с динамическими («подвижными»). Динамическое равновесие устанавливается, когда оказываются сбалансированными два обратимых или противоположных процесса. Динамические равновесия подразделяют на физические и химические. Наиболее важными типами физических равновесий являются фазовые равновесия. Система находится в состоянии химического равновесия, если скорость прямой реакции равна скорости обратной реакции.

Например, если скорость протекания реакции (константа скорости к₁)

k₁

А_(г) + В_(пар) 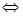 АВ_(г)

равна скорости обратной реакции (константа скорости k₂)

k₂

АВ(г) 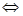А_(г) + В_(пар)

то система находится в динамическом равновесии. Подобные реакции называются обратимыми, а их уравнения записывают с помощью двойной стрелки:

k₁

А_(г) + В_(пар) 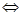 АВ_(г)

k₂

Реакции, протекающие слева направо, называются прямой, справа налево – обратной.

Нужно подчеркнуть, что реакционная система остается в состоянии динамического равновесия лишь до тех пор, пока система остается изолированной. Изолированной называют такую систему, которая не обменивается с окружающей средой ни веществом, ни энергией.

Состояние химического равновесия обратимых процессов количественно характеризуется константой равновесия. Так, для обратимой реакции общего вида

k₁

аA +bB 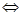 сC + dD (1.2.1)

k₂

константа равновесия К, представляющая собой отношение констант скорости прямой и обратной реакций, запишется

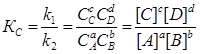 (1.2.2)

где, К_с – константа скорости реакции, зависящая от концентрации реагирующих компонентов; С _i или [ i ]- равновесная молярная концентрация i -того компонента;

a , b , c , d – стехиометрические коэффициенты веществ.

В правой части уравнения (1.2.2) стоят концентрации взаимодействующих частиц, которые устанавливают при равновесии, - равновесные концентрации.

Уравнение (1.2.2) представляет собой математическое выражение закона действующих масс при химическом равновесии. Для реакции с участием газов константа равновесия выражается через парциальные давления, а не через их равновесные концентрации. В этом случае константу равновесия обозначают символом К_р.

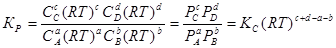
Р _i - равновесные парциальные давления i-того компонента.

С _i - равновесная молярная концентрация компонентов.

a , b , c , d – стехиометрические коэффициенты веществ.

Состояние химического равновесия при неименных внешних условиях теоретически может сохраняться бесконечно долго. В реальной действительности, т.е. при изменении температуры, давления или концентрации реагентов, равновесии может «сместиться» в ту или иную сторону протекания процесса.

Изменения, происходящие в системе в результате внешних воздействий, определяется принципом подвижного равновесия – принципом Ле Шателье – Брауна. При воздействие на равновесную систему, любого внешнего фактора, равновесие в системе смещается в таком направлении, чтобы уменьшить воздействие этого фактора.

1. Влияние давления на равновесие химической реакции (для реакции, проходящей в газовой фазе).

aA + bB 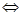cC + dD

- если реакция идет с увеличением количества компонентов a + b < c + d, то повышение давления смещает равновесие химической реакции справа налево.

- если реакция идет с уменьшением количества компонентов a + b > c + d, при увеличении давления сдвиг равновесия произойдет слева направо.

- если количество компонентов одинаково a + b = c + d, то изменение давления не повлияет на положении равновесия.

2. Влияние инертного газа. Введение инертного газа подобно эффекту уменьшения давления (Ar, N₂, водяной пар). Инертный газ не участвует в реакции.

3. Влияние изменения концентрации реагирующих веществ. При введение дополнительного количества вещества равновесие химической реакции сместиться в ту сторону где концентрация вещества уменьшается.

4. Влияние температуры на химическое равновесие реакции.

Если к равновесной системе подводится теплота, то в системе происходят изменения, чтобы ослабить это воздействие, т.е. процессы с поглощением теплоты. При экзотермических реакциях снижение температуру сместит равновесие слева направо, а при эндотермических реакциях повышение температуры сместит равновесие справа налево.

Зависимость К_р от температуры – уравнение Вант – Гоффа.

; ;

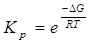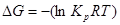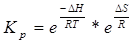( ); lnk_{T 1} – lnk_{T 2} =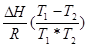

Примеры решения задач

1. Реакция соединения азота и водорода обратима и протекает по уравнению

N₂ + 3Н₂ 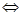2NН₃. При состоянии равновесия концентрации участвующих в ней веществ были: [N₂] = 0,01 моль/л, [Н₂] = 2,0 моль/л, [NH₃] = 0,40 моль/л. Вычислить константу равновесия и исходные концентрации азота и водорода.

Решение:

Для приведенной реакции

 

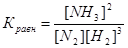
Подставляя значение равновесных концентраций, получим

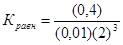= 2

Согласно уравнению реакции из 1 моль азота и 3 моль водорода получаем

2 моль аммиака, следовательно, на образование 0,4 моль аммиака пошло

0,2 моль азота и 0,6 моль водорода. Таким образом, исходные концентрации будут [N₂] = 0,01 моль/л + 0,2 моль/л = 0,21 (моль/л),

[H₂] = 2,0 моль/л + 0,6 моль/л = 2,6 (моль/л).

Ответ: К_равн = 2; С₀ (N₂) = 0,21 моль/л и С₀ (Н₂) = 2,6 моль/л.

2. Один моль смеси пропена с водородом, имеющей плотность по водороду 15, нагрели в замкнутом сосуде с платиновым катализатором при 320°С, при этом давление в сосуде уменьшилось на 25%. Рассчитайте выход реакции в процентах от теоретического. На сколько процентов уменьшится давление в сосуде, если для проведения эксперимента в тех же условиях использовать 1 моль смеси тех же газов, имеющей плотность по водороду 16?

Решение:

С₃Н₆ + Н₂ 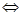С₃Н₈

1) Пусть ν(C₃H₆) = х, ν(H₂) =1-x, тогда масса смеси равна

42х + 2(1 - х) = 2 • 15 = 30,

откуда х = 0,7 моль, т. е. ν(C₃H₆) = 0,7 моль, ν(H₂) = 0,3 моль.

Давление уменьшилось на 25% при неизменных температуре и объеме за счет уменьшения на 25% числа молей в результате реакции. Пусть у моль Н₂ вступило в реакцию, тогда после реакции осталось:

ν(C₃H₆) = 0,7 - у, ν(H₂) = 0,3 – у, ν(C₃H₈) = у,

ν_о6щ = 0.75 =(0,7 - у) + (0,3 - у) + у, откуда y = 0,25 моль.

Теоретически могло образоваться 0,3 моль С₃Н₈ (H₂ — в недостатке), поэтому выход равен 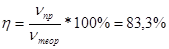. Константа равновесия при данных условиях равна

   

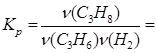
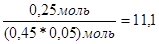
2) Пусть во втором случае ν(C₃H₆) = a моль, ν(H₂) = (1 – а) моль, тогда масса смеси равна 42а + 2(1 - а) = 2 • 16 = 32, откуда, а= 0,75, т. е. ν(C₃H₆) = 0,75, ν(H₂) = 0,25. Пусть в реакцию вступило b моль Н₂. Это число можно найти из условия неизменности константы равновесия

=  

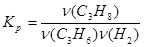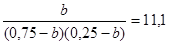
Из двух корней данного квадратного уравнения выбираем корень, удовлетворяющий условию 0 < b < 0,25, т. е. b = 0,214 моль

Общее число молей после реакции равно

ν_oбщ =((0,75 - 0,214) + (0,25 - 0,214) + 0,214 - 0,786) моль, т. е. оно уменьшилось на 21,4% по сравнению с исходным количеством (1 моль). Давление пропорционально числу молей, поэтому оно также уменьшилось на 21,4%.

Ответ: выход С₃Н₈ — 83,3%; давление уменьшится на 21,4%.

Задачи для самостоятельного решения

1. В реакции между раскаленным железом и паром

3Fe_(тв) + 4Н₂О_(г) 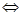Fe₃O_4(тв)+4Н_2(г), при достижении равновесия парциальные давления водорода и пара равны 3,2 и 2,4 кПа соответственно. Рассчитайте константу равновесия.

2. Вычислите константы равновесия К_р К_С газовой реакции

СО + Cl₂ 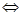 СОCl_2, состав газовой смеси при равновесии был следующим (% по объему): СО=2,4, Cl₂ =12,6, СОCl₂ =85,0, а общее давление смеси при 20С составляло 1,033*10⁵ Па. Вычислите ΔG реакции.

3. Рассчитайте константу равновесия при некоторой заданной данной температуре для обратимой реакции СО + Н₂О 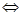СО₂ + Н₂, учитывая, что в состоянии равновесия концентрации участвующих в реакции веществ были равны [СО] = 0,16 моль/л, [Н₂О] = 0,32 моль/л, [СО₂] = 0,32 моль/л, [Н₂] = 0,32 моль/л.

4. В стальном резервуаре находятся карбонат кальция и воздух под давлением 1 атм. при температуре 27°С. Резервуар нагревают до 800°С и дожидаются установления равновесия. Вычислите константу равновесия К_р реакции CaCO₃ 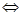СаО + СО₂ при 800°С, если известно, что равновесное давление газа в резервуаре при этой температуре равно 3,82 атм., а при 27°С СаСО₃ не разлагается.

5. При постоянной температуре в гомогенной системе А + В = 2С установилось равновесие с равновесными концентрациями [А]=0,8 моль/ль, [В]=0,6 моль/л, [С]=1,2 моль/л. определите новые равновесные концентрации, если в систему дополнительно ввели 0,6 моль/л вещества В.

6. Как можно обосновать оптимальные условия промышленного синтеза аммиака с высоким выходом на основе термохимического уравнения реакции

N₂ + ЗН₂ 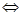 2NH₃ + 491,8 кДж и с учетом того, что при низких температурах скорость прямой реакции очень мала?

7. Вычислите константу равновесия ниже приведенных реакции, протекающей при стандартных условиях и при 400К.

а) Na₂O_(к) + CO_2(г) → Na₂CO_3(к)

б) N₂O_4(г) = 2NO_2(г)

8. Уравнение реакции окисления хлорида водорода

4НСl _(г) + O_2(г) = 2H₂O_(г) + 2Cl_2(г) Вычислите константу равновесия этой реакции при Т=500К. Предположите способы увеличения концентрации хлора в равновесной смеси.

9. При смешении 2 моль уксусной кислоты и 2 моль этилового спирта в результате реакции СН₃СООН + С₂Н₅ОН = СН₃СООС₂Н₅ + Н₂О к моменту наступления равновесия осталось 0,5 моль СН₃СООН и С₂Н₅ОН, а также некоторое количество эфира и воды. Определите состав равновесной смеси, если смешивают по 3 моль СН₃СООН и С₂Н₅ОН при той же температуре.

10. Вычислить начальные концентрации веществ в обратимой реакции

2СO +О₂ 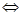2СО₂ и константу равновесия, если равновесные концентрации составляют [СО]=0,44 моль/л, [О₂]=0,12 моль/л, [СО₂] =0,18 моль/л.

Химическая кинетика

Это раздел физической химии, изучающей скорость химических реакций, а в более широком смысле – закономерности их протекания.

Термин скорость реакции означает скорость, с которой образуются продукты, либо скорость, с которой расходуются агенты при протекании химической реакции. Химические реакции происходят с самыми разными скоростями. Со скоростью химических реакций связаны представления о превращении веществ, а также экономическая эффективность их получения в промышленных масштабах. Основным понятием в химической кинетике является понятие о скорости реакции, которая определяется изменением количества вещества реагентов (или продуктов реакции) в единицу времени в единице объема. Если при неизменном объеме и температуре концентрация одного из реагирующих веществ уменьшилась (или увеличилась) от значения с₁ до значения с₂ за промежуток времени от t₁ до t₂, то средняя скорость реакции составит

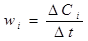 (1.3.1)

где D С _i – изменения концентрации i-того компонента, моль/м³ или моль/л,

w_i - скорость реакции, (моль/(л • с) или моль/м³ *с). Уравнение (1.3.1) подходит для реакций протекающих в гомогенном реакционном пространстве.

Если реакция протекает в гетерогенном пространстве, то выражение для скорости реакции по данному веществу i имеет вид (моль/м³ *с).

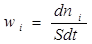 (1.3.2)

dn_i – изменение количества i-того компонента, моль; S- площадь, м^2;

dt – изменение времени, с.

I . Продукты реакции или промежуточные соединения образуются при взаимодействии частиц в элементарном химическом акте. Число частиц в элементарном химическом акте называется молекулярностью реакции. Элементарные реакции бывают трех типов:

- мономолекулярные А ® Р₁+ Р₂ + …

- бимолекулярные А + В ® Р₁+ Р₂ +...

- тримолекулярные 2А + В ® Р₁+ Р₂ + … 3А ® Р₁+ Р₂ + …,

А + В + С ® Р₁+ Р₂ + …

Четырехмолекулярных реакций не бывает, т.к. вероятность одновременного столкновения четырех молекул ничтожно мала.

Скорость реакции можно измерить, определяя количество реагента или продукта во времени. Скорость реакции зависит от природы реагирующих веществ и от условий, в которых реакция протекает. Важнейшими из них являются концентрация, температура и присутствие катализатора.

Рассмотрим реакцию между веществами А и В, протекающую по схеме

аА + вВ + …. → сС + dD + …

Скорость реакции зависит от концентраций А и В, однако заранее нельзя утверждать, что она прямо пропорциональна концентрации того или другого. Зависимость скорости химической реакции от концентрации реагирующих веществ выражается основным законом химической кинетики — законом действующих масс: скорость элементарной химической реакции прямо пропорциональна произведению концентрации реагирующих веществ в степенях, равных стехиометрическим коэффициентам в уравнении реакции.

Для элементарной реакции

n₁А + n₂В ® n₃С + n₄Е + …

w= 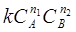или w = k [A]^nA [B]^{n В}. (1.3.3)

Выражение такого типа называют кинетическим уравнением, где k - константа скорости (не зависит от концентрации реагирующих реагентов и времени); C_A , C_B – текущие концентрации реагирующих веществ; n _1, n ₂ - некоторые числа, которые называются порядком реакции по веществам А и В соответственно. Порядок реакции совпадает со стехиометрическими показателями элементарной реакции. Порядок реакции n – сумма показателей кинетических степеней в химическом уравнении реакции. Сумма показателей степеней n ₁ + n₂ = n называется общим порядком реакции. Для элементарной реакции общий порядок равен молекулярности, а порядок по веществам равны коэффициентам в уравнении реакции. Порядок реакции по i-тому компоненту не равен его стехиометрическому коэффициенту в химическом уравнении сложной реакции.

1. Реакции нулевого порядка. Скорость этих реакций не зависит от концентрации реагирующего вещества n=0. Из уравнений 1.3.1 и 1.3.3 получим следующее

w = k или 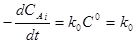. (1.3.4)

Интегрируя выражение (1.3.4) получаем:

C_A,t=C_A,0 – k₀t, k₀t = C_A,0 – C_A,t (1.3.5)

Введем понятие время полупревращения t _1/2 – это время, в течение которого превращается половина исходного вещества.

Для реакции нулевого порядка в уравнение 1.3.5 подставим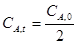

t _1/2 =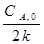

2. Реакции первого порядка. Для реакции первого порядка n=1 типа

А ® Р₁+ Р₂ + …, скорость прямо пропорциональна концентрации вещества А:

w = ;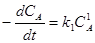

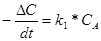
lnC_{A , t} = lnC_{A ,0} – kt

С=С_{А, t} = C_{A ,0} e ^{- kt}

t _1/2=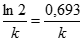

3. Реакции второго порядка. Для реакции второго порядка n=2 типа

А + В ® Р₁+ Р₂ +..., если С_А,0=С_В,0 кинетическое уравнение имеет вид

w= ;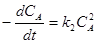

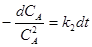
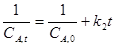
t_1/2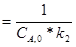

Для реакции второго порядка типа А + В ® Р + … если С_А,0 ¹ С_В,0 кинетическое уравнение имеет вид

w =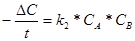

Периоды полураспада вещества А и В, если С_А,0 ¹ С_В,0, различны,

т.е. t _1|2 ( A ) ¹ t _1|2 ( B ).

4. Реакции третьего порядка. Кинетика реакции третьего порядка n=3 типа

2А + В ® Р₁+ Р₂ + … 3А ® Р₁+ Р₂ + …, А + В + С ® Р₁+ Р₂ + …

при равных начальных концентрациях описывается уравнением

w =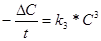

t _1|2 =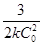

Для реакции А + В + С ® Р + …,если С_А,0 ¹ С_В,0¹С_С,0 кинетическое уравнение примет вид

w=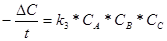

II . Выражение (1.3.1) записано для фиксированной температуры. Для приближенной оценки изменения скорости широко используется эмпирическое правило Вант-Гоффа, в соответствии с которым скорость химической реакции становится в 2-4 раза больше при повышении температуры на каждые 10°C. В математической форме зависимость изменения скорости реакции от температуры выражается уравнением

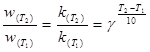 (1.3.4)

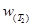— скорость реакции при повышенной температуре Т₂,

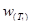- скорость реакции при начальной температуре Т₁; γ —температурный коэффициент скорости, показывающий, во сколько раз увеличится скорость реакции при повышении температуры на 10°С (2-4). Это позволяет предположить, что между скоростью реакции и температурой должна существовать экспоненциальная зависимость. Точное соотношение между скоростью реакции и температурой установил шведский химик Аррениус в 1899 г. Это соотношение, получившее название уравнение Аррениуса, имеет вид

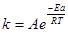 (1.3.5)

где k – константа скорости реакции; А — постоянная, характеризующая каждую конкретную реакцию (константа Аррениуса, или «предэкспонента»);

Е_a — постоянная, характерная для каждой реакции и называемая энергией активации, Дж; R — универсальная газовая постоянная Дж/(К*моль);

Т — температура, К.

Подчеркнем, что это уравнение связывает температуру не со скоростью реакции, а с константой скорости. Приведем уравнение Аррениуса для двух температур

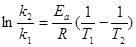
III . Одно из наиболее сильных средств влияния на скорость реакции — присутствие в реагирующей системе катализатора - вещества, которое усиливают (а иногда и понижают - тогда его называют ингибитором) скорость химической реакции, но само не расходуется в этом процессе.

Примеры решения задач

1. Во сколько раз увеличится скорость химической реакции при повышении температуры с 0 до 50°С, принимая температурный коэффициент скорости равным трем?

Решение: