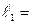Найдем выражение для периода колебаний математического маятника. Выше мы выяснили, что маятник совершает колебания под действием возвращающей силы:
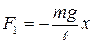
Эта сила является квазиупругой, поэтому ее можно выразить формулой:
 ,
,
где 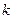 - коэффициент квазиупругой силы.
- коэффициент квазиупругой силы.
Очевидно, что 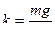 (5)
(5)
Коэффициент 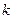 связан с циклической частотой
связан с циклической частотой 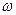 и массой
и массой 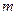 соотношением:
соотношением:
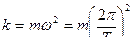 (6)
(6)
Решая совместно уравнения (5) и (6), получим формулу для периода Т колебания математического маятника:
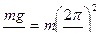 , отсюда
, отсюда
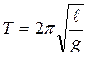 , (7)
, (7)
где 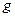 - ускорение силы тяжести;
- ускорение силы тяжести;
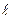 - длина математического маятника.
- длина математического маятника.
Эту формулу можно применять как к математическому, так и к физическому маятнику, но для физического маятника длина обозначает так называемую приведенную длину физического маятника. Приведенной длиной физического маятника называется длина некоторого воображаемого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.
На практике приведенная длина физического маятника определяется расстоянием между точкой подвеса маятника и его центром качания.
Центр качания лежит ниже центра тяжести маятника. Маятник, вся масса которого была бы сосредоточена в центре качания, имел бы тот же период, что и математический маятник данной длины.
Период Т колебаний физического маятника
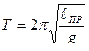 ,
,
где 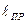 - приведенная длина маятника.
- приведенная длина маятника.
Решая эту формулу относительно 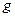 , будем иметь:
, будем иметь:
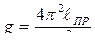 (8)
(8)
Маятник, применяемый в работе, представляет собой массивный шарик небольшого радиуса, подвешенный на длинной нити, чтобы колебания происходили строго в одной плоскости.
В данном случае конструктивное оформление установки следующее: на перекладине между двумя жестко укрепленными вертикальными стойками подвешен на двойной нити свинцовый шарик А. Вдоль вертикальных стоек перемещается при помощи скользящих муфт вторая горизонтальная перекладина – линейка В, которая может быть закреплена на любой высоте при помощи винта в одной из муфт. На стойках миллиметровая шкала (рис. 1).
Приведенной длиной маятника следует считать расстояние от точки подвеса О до центра качания шарика. Однако непосредственно определить приведенную длину маятника сложно, поэтому поступают следующим образом: подводят подвижную линейку до соприкосновения с шариком и измеряют длину  ,
,
где 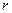 - радиус шарика, и длину
- радиус шарика, и длину  .
.
Затем рассчитывают периоды колебаний 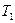 и
и 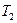 маятников двух различных приведенных длин
маятников двух различных приведенных длин 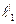 и
и  .
.
Из формулы (8) имеем:
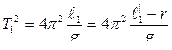 (9)
(9)
 (10)
(10)
Вычитая (10) из (9), получим:
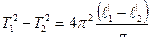 , откуда
, откуда
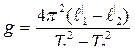 (11)
(11)
Таким образом, для определения 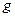 по формуле (11) нужно измерить лишь разности длин
по формуле (11) нужно измерить лишь разности длин 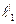 и
и  маятников и периоды
маятников и периоды 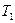 и
и 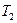 их колебаний. При таком способе измерения исключается необходимость измерения центра качания шарика.
их колебаний. При таком способе измерения исключается необходимость измерения центра качания шарика.
Порядок выполнения работы
1. Установить определенную длину маятника.
2. Линейкой измерить длину 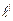 от точки подвеса до нижнего края шарика.
от точки подвеса до нижнего края шарика.
3. Отвести маятник от положения равновесия на небольшой угол ( 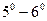 ), отпустить шарик. В момент наибольшего отклонения маятника включить секундомер и измерить время
), отпустить шарик. В момент наибольшего отклонения маятника включить секундомер и измерить время 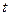 , за которое маятник совершит 50 полных колебаний.
, за которое маятник совершит 50 полных колебаний.
4. Измерение времени при неизменной длине 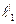 произвести три раза и среднее значение занести в таблицу.
произвести три раза и среднее значение занести в таблицу.
5. Произвести такие же измерения еще для двух других длин маятников  и
и  .
.
6. По результатам измерений рассчитать периоды колебаний 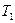 ,
, 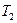 и
и 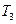 по формуле
по формуле 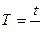 .
.
7. Вычислить три значения 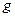 , пользуясь формулой (11).
, пользуясь формулой (11).
8. Данные опытов занести в таблицу
9. Рассчитать среднее значение 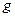 , абсолютную и относительную погрешности.
, абсолютную и относительную погрешности.
| № опыта | 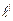
| 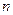
| 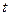
| 
| Т | 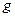
| 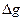
| 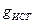
| 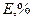
|
|
1
|
|
|
|
|
|
|
|
| |
|
2
|
|
|
|
|
|
|
|
| |
|
3
|
|
|
|
|
|
|
|
| |
              Ср.
знач. Ср.
знач.
|
Контрольные вопросы
1. Какие колебания называются гармоническими?
2. Дайте определение амплитуды, частоты, периода, циклической частоты.
3. Дайте определение математического маятника.
4. Выведите уравнение колебаний математического маятника.
5. Выведите формулу для периода колебаний математического маятника.
6. От чего зависят ускорение силы тяжести?
Литература [ 2,6,7]

О
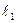
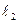
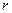
А
В
Рисунок 2 – Лабораторная установка «Математический маятник»
ЛАБОРАТОРНАЯ РАБОТА № 22
Дата: 2019-07-24, просмотров: 372.