Цель работы: ознакомление с характером собственных колебаний и выяснение основных характеристик механических колебательных систем, определяющих процесс собственных колебаний.
Задачи работы:
1) определить: коэффициент упругости пружины;
2) исследовать зависимость периода собственных колебаний пружинного маятника от массы маятника;
3) определить логарифмический декремент затухания;
4) исследовать зависимость логарифмического декремента затухания от силы тока в катушке электромагнита.
Приборы и принадлежности: пружинный маятник, секундомер, набор грузов различной массы, электромагнит, выпрямитель.
Теория метода и описание установки
Для выполнения работы необходимо предварительно изучить тему “Механические колебания “.
В данной работе рассматриваются собственные незатухающие колебания простейшей колебательной системы - пружинного маятника. Он представляет собой груз массой m , подвешенный на упругой пружине. Будем считать, что масса пружины мала по сравнению с массой груза.
Лабораторная установка состоит из штатива со шкалой. К штативу прикреплена пружина с подвешенным к ней грузом в форме полого медного цилиндра. Масса цилиндра указана на установке. Амплитуда колебаний маятника измеряется по вертикальной шкале.
При подвешивании к пружине груза массой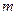 
она удлинится на величину 
, называемую статическим удлинением пружины. Когда маятник находится в состоянии равновесия, сила тяжести уравновешивается силой упругости пружины:
mg = - k 
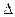x.
Отсюда коэффициент упругости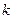 
равен: 
(1)
Если пружинный маятник вывести из состояния равновесия, слегка оттянув пружину вниз, то он будет совершать собственные колебания под действием упругой силы
F = -kx , (2)
где k - коэффициент упругости;
x - смещение.
Эта сила сообщает маятнику ускорение и равна
F = ma , (3)
где a - ускорение;
m - масса маятника.
Уравнение собственных колебаний маятника запишется в виде:
-kx = ma (4)
Ускорение a = - w2 x , где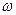 
- циклическая частота.
Подставив это выражение в уравнение (4), получим:
-kx = - mw2 x
или k = mw2 (5).
Циклическую частоту w выразим через период Т колебаний и, подставив в (5), найдем период колебаний пружинного маятника:
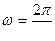
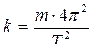, отсюда 
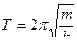(6)
Период колебаний пружинного маятника не зависит от амплитуды колебаний, а зависит от массы и коэффициента упругости пружины.
Рисунок 1 – пружинный маятник
Задание I. Определение коэффициента упругости пружины.
1. Заметить по вертикальной шкале начальное отклонение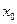 
маятника.
2. Подвесить добавочный груз массой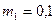 
кг и снова заметить отклонение
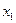маятника.
3. Найти удлинение пружины 
, вызванное добавочным грузом
массой 
.
4. По формуле 
рассчитать коэффициент упругости.
5. Повторить пункты 1-4 с грузами массами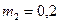 
кг и 
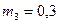кг.
6. Найти среднее значение коэффициента упругости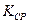 
и оценить погрешности.
7. Результаты измерений и вычислений занести в таблицу:
| № опыта | 
|
| 
|
|
| 
| 
| 
|
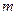
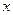
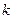
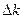
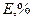
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
     Ср. зн.
|
Задание II. Исследование зависимости периода собственных колебаний
пружинного маятника от массы.
1. Снять добавочные грузы, оттянуть кольцо слегка вниз и отпустить. Секундомером измерить время t десяти полных колебаний (n = 10).
2. Рассчитать период Т собственных колебаний по формуле: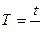 
3. Повторить опыты еще 2 раза, подвешивая добавочные грузы 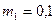кг и 
=0,2 кг.
4. Результаты измерений и вычислений занести в таблицу.
5. Построить график зависимости 
.
6. Используя значения периода Т, полученные опытным путем, вычислить коэффициент упругости по формуле:
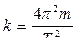
и сравнить его со значением коэффициента упругости, полученным статическим методом в 1-м задании.
Таблица1. Результаты измерений и расчётов
| № опыта |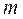 
| 
| 
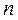
| Т |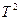 
|
| 1 | |||||
| 2 | |||||
| 3 |
Задание III. Определение логарифмического декремента затухания.
При выполнении этого задания в установке используются силы магнитного взаимодействия. Кольцо с добавочным грузом движется во время колебаний вдоль оси стержня электромагнита, питаемого постоянным током от выпрямителя. При этом в кольце наводится индукционный ток, магнитное поле которого в соответствии с правилом Ленца создает тормозящее действие.
Приближенно можно считать, что сила сопротивления пропорциональна скорости движения кольца. Следовательно, маятник должен совершать затухающие колебания с коэффициентом затухания b и логарифмическим декрементом затухания l.
Порядок выполнения
1. Подвесить к маятнику два 100-грамовых груза.
2. Оттянуть маятник от положения равновесия на 27 мм (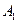 
= 27 мм).
3. Отпустить маятник и посчитать число полных колебаний n до тех пор, пока амплитуда станет равной 10 мм ( 
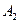= 10 мм), т.е. уменьшится в е=2,7 раз.
4. Определить логарифмический декремент затухания по формуле:
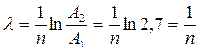
5. Повторить опыты, устанавливая последовательно токи питания электромагнита 0,5 А; 1 А; 1,5 А; 2 А.
6. По полученным результатам построить график зависимости l = f (I)
Таблица 2. Результаты измерений и расчётов задания III
| № опыта | I,А |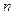 
| 
|
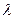
| 1 2 3 4 5 | 0 0,5 1 1,5 2 |
Контрольные вопросы
1. Дайте определение гармонических колебаний и их кинематических характеристик ( амплитуды, фазы, периода. частоты, циклической частоты).
2. Запишите формулу для периода колебаний пружинного маятника.
3. Запишите кинематическое и динамическое уравнения затухающих колебаний.
4. Каков физический смысл коэффициента затухания b?
5. Что называется логарифмическим декрементом затухания и какой его физический смысл?
Литература [ 2,6,7]
ЛАБОРАТОРНАЯ РАБОТА № 20
Дата: 2019-07-24, просмотров: 304.
