Система, состоящая из генератора электромагнитных колебаний и двух близко расположенных друг к другу параллельных проводов, называют системой Лехера. Такую систему можно рассматривать как колебательный контур с распределенными параметрами. Механизм распространения электромагнитных волн в двухпроводной линии таков. На рис.1 приведен случай, когда генератор подключен к двухпроводной линии в точках А и В.

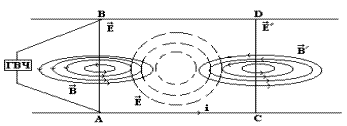
Рисунок 1 – Схема подключения генератора к двухпроводной линии

Тогда между этими точками возникает переменное электрическое поле Е. Это поле создаст в пространстве переменное магнитное поле индукции В, величину и направление которого можно определить, применив правило буравчика. В свою очередь, изменяющееся магнитное поле создает, в пространстве переменное вихревое электрическое поле Е. Процесс взаимного превращения электрического и магнитного полей будет продолжаться непрерывно.

Таким образом, в пространстве появляются электромагнитные волны. Направления векторов Е и В электромагнитной волны перпендикулярны к скорости распространения волны u.

В двухпроводной линии энергия электромагнитной волны передается полностью от источника в нагрузку (через двухпроводную линию) только тогда, когда в линии нет потерь и отражений энергии. В этом случае в системе Лехера существуют только бегущие волны, где волны электрического и магнитного полей совпадают по фазе и в проводах несутся волны тока и напряжений. Их амплитуды не зависят от координат ОХ, а плотность переносимой энергии определяется вектором Умова – Пойтинга 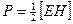. Такая ситуация в системе Лехера возникает если двухпроводная линия либо бесконечно длинная, либо замкнута конечным сопротивлением, известное как волновое сопротивление. Последнее равно отношению амплитуд напряжения и тока в бегущей волне. Если считать, что тепловые потери тока в линии малы, а утечка между проводами незначительна, то приближенно волновое сопротивление равно

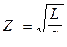                           ,                                                         (1)

Так как индуктивность единицы длины линии L и емкость С зависят от геометрических размеров и их взаимного расположения , то волновое сопротивление можно выразить через геометрические размеры линии в таком виде

                               Z = 276 lоq( a/d),                                            (2)

где а - расстояние между проводами, d - диаметр провода.

Если линия закорочена (R = 0) или разомкнута (R = 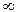 ), на конце линии происходит полное отражение энергии и в линии устанавливается стоячая волна.

Если нагрузить линию на конце сопротивлением большим или меньшим волнового (R ¹ Z), то появится отраженная волна и наряду с бегущей волной в линии установится и стоячая волна.

Необходимо иметь в виду, что в реальных двухпроводных линиях не могут быть практически осуществлены режимы чисто бегущих или чисто стоячих волн. Причины этого состоят в наличии во всякой реальной линии отражений и потерь, связанных с выделением джоулева тепла и излучением электромагнитной энергии в окружающую среду. Таким образом, в реальной двухпроводной линии всегда имеет место смешанный режим бегущих и стоячих волн.

Процесс образования стоячих волн в двухпроводной линии конечной длины происходит следующим образом (для простоты рассмотрим только электрическую составляющую электромагнитной волны). Запишем уравнение для электрического вектора плоской волны, распространяющейся в положительном направлении оси ОХ (уравнение бегущей волны):

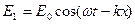                         ,                                                      (2а)

где 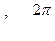 - волновое число,  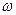- частота, Е₀ - амплитудное значение вектора электрического поля. Тогда для отраженной волны соответствующее уравнение будет иметь вид

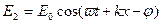                              ,                                           (2б)

где 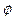 - фазовый сдвиг между бегущей и отраженной волнами. Будем считать, что отражение происходит без потерь энергии, поэтому амплитуда падающей и отраженной волн одинаковы. Обе волны складываясь, образуют стоячую волну

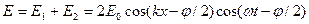                            ,                  (3)

Как это следует из выражения (3), если на длине линии укладывается целое число полуволн, то фазовый сдвиг будет постоянным. Тогда в линии образуется стоячая волна, амплитуда которой равна 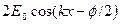, что уже является функцией от координаты X. Вид этой функции показан на рис.2 .

Рисунок 2 – Зависимость амплитуды стоячей волны от координаты х

Амплитуда колебаний вектора Е в стоячей волне обращается в нуль в точках, для которых 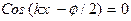. Эти точки называются узлами электрического поля стоячей волны. По середине между двумя соседними узлами в точке, где  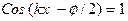амплитуда колебаний максимальна. Такие точки называются пучностями электрического вектора стоячей волны. В стоячей волне не происходит передача энергии через узлы или пучности волны и имеет место только локальное возбуждение. 

В стоячей волне колебания векторов Е и В не будет совпадать по фазе, как это было для бегущей волны. Характер распределения узлов и пучностей электрического и магнитного полей в стоячей волне зависит от условий на концах линии, т.е. от граничных условий.

Рассмотрим двухпроводную линию, один конец которой разомкнут, а второй - индуктивно связан с генератором высокой частоты (рис.4). Так как разомкнутый конец граничит с диэлектриком , то, по закону Ома, амплитуда тока на конце линии будет равна нулю, а значит, здесь будет находится узел магнитного поля В и, следовательно, пучность электрического поля Е т.е. пучность напряжения. (рис 3, 4а).

Рисунок 3 – Пучность напряжения электрического поля

Если линия закорочена (R=0), то амплитуда напряжения на конце линии будет равна нулю, а значит, здесь будет находится узел электрического поля Е и, следовательно, пучность магнитного поля В т.е. образуется пучность тока и узел напряжения (см.рис.4 б).

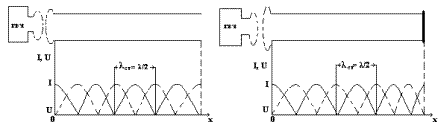
а)                             б)

Рисунок 4 – Пучность тока и узел напряжения