На изменение среднего значения показателя могут оказывать воздействие одновременно два фактора: изменение значений усредняемого показателя и изменение структуры явления. Требуется определить степень влияния этих двух факторов.
Такая задача решается с помощью индексного метода, т.е. путем построения системы следующих взаимосвязанных индексов:
· переменного состава;
· постоянного состава;
· структурных сдвигов.
Если в числителе и знаменателе сводного индекса веса берутся (фиксируются) на уровне одного и того же периода, то он называется индексом фиксированного состава и определяется по формуле:
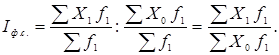 (1.30)
(1.30)
Индекс переменного состава представляет собой соотношение средних уровней изучаемого явления. Если индекс постоянного (фиксированного) состава показывает среднее изменение лишь одной индексируемой величины, то индекс переменного состава характеризует общее изменение средней как в результате изменения индивидуальных значений индексируемой величины, так и в результате изменения структуры совокупности (весов). Индекс переменного состава определяют по формуле:
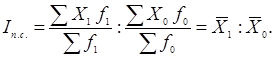 (1.31)
(1.31)
Для отражения влияния изменений в структуре изучаемой совокупности на динамику изучаемого явления вычисляется индекс структуры (структурных сдвигов) по формуле:
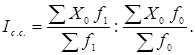 (1.32)
(1.32)
Взаимосвязь между индексами
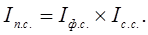 (1.33)
(1.33)
При изучении товарооборота используют:
- индекс цен фиксированного состава
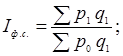 (1.34)
(1.34)
- индекс переменного состава
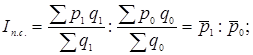 (1.35)
(1.35)
- индекс структурных сдвигов
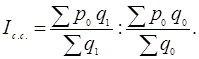 (1.36)
(1.36)
Индекс постоянного состава характеризует динамику средней величины при одной и той же фиксированной структуре совокупности, т.е. он определяется как отношение двух средневзвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя только за счет самой индексируемой величины (в однородной совокупности).
Здесь элиминировано (устранено) влияние изменения структуры совокупности на динамику средней величины.
Индекс структурных сдвигов исчисляется как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру отчетного периода, к фактической средней этого показателя в базисном периоде. Он используется для определения влияния только структурных изменений на исследуемый средний показатель.
Пример . По данным табл. 1.5 нужно рассчитать влияние структурных сдвигов на изменение средней себестоимости двух однотипных изделий.
Таблица 1.5 - Показатели затрат
| Изделие | Себестоимость, руб. | Произведено, тыс. шт. | ||
| базисный период с0 | отчетный период с1 | базисный период q 0 | отчетный период q 1 | |
| 1 | 2,3 | 2,1 | 91,5 | 137,8 |
| 2 | 1,9 | 2,1 | 170,3 | 101,6 |
Рассчитаем индекс себестоимости переменного состава:
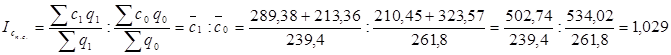
или 102,9%.
Под влиянием изменения индивидуальных себестоимостей и структурных сдвигов в производстве данных изделий средняя себестоимость увеличилась на 2,9 %.
Индекс себестоимости фиксированного состава:
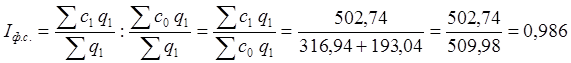
или 98,6%.
Под влиянием изменения индивидуальных себестоимостей средняя себестоимость снизилась на 1,4 %.
Этот, казалось бы, противоречивый результат получился из-за структурных сдвигов.
Индекс структуры
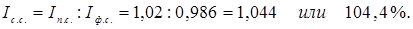
Это значит, что вследствие изменения структуры произведенной продукции себестоимость увеличилась на 4,4 %.
Дата: 2019-07-24, просмотров: 505.