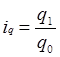В агрегатных индексах качественных показателей индексируемой величиной является качественный показатель, а весом индекса (соизмерителем) выбирается количественный показатель. При этом качественный показатель в числителе и знаменателе индекса принимается на разных уровнях (индексируется), а вес индекса – на одном неизменном временном уровне.
К индексам качественных показателей относятся индексы цен, себестоимости, трудоемкости продукции, производительности труда и т.п.
В условиях рыночных отношений особое место среди индексов качественных показателей занимает индекс цен.
При помощи индекса потребительских цен (ИПЦ) производится оценка динамики цен на товары производственного и непроизводственного потребления. Он отражает динамику цен конечного потребления, измеряет общую стоимость фиксированного набора потребительских товаров и услуг, который называется потребительской корзиной, а также является одним из важнейших показателей, характеризующих уровень инфляции. ИПЦ используется при корректировке законодательно устанавливаемых минимального размера оплаты труда, ставок налога и т.д.
Поскольку индекс характеризует изменение цен, то индексируемой величиной является цена, а весом – количество товаров одного из периодов.
Сводный индекс цен определяют по формуле:
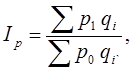(1.9)
где 
– цена отдельных видов продукции соответственно в отчетном и базисном периодах (индексируемый показатель);
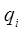– объем реализованной продукции в i -м периоде (вес индекса).
Данный индекс характеризует, как изменились цены в среднем на различные виды продукции в анализируемой совокупности.
В 1864 году немецкий экономист Э. Ласпейрес предложил индекс, который отражает изменение цен и строится по продукции базисного периода. Формула агрегатного индекса цен Ласпейреса представляет собой следующее соотношение:
 |
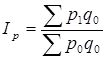, (1.10)
где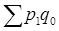 
- условная стоимость товаров, которые реализованы в базисном периоде по отчетным ценам;
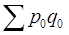- фактическая стоимость продукции базисного периода.
Индекс Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде.
В 1874 году немецкий экономист Г.Пааше впервые предложил агрегатный индекс цен с отчетными весами. Формула агрегатного индекса цен Пааше выглядит следующим образом:
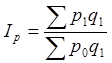, (1.11)
где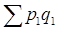 
- фактическая стоимость продукции отчетного периода;
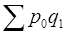- условная стоимость товаров, которые реализованы в отчетном периоде по базисным ценам.
Индекс цен Пааше показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или на сколько процентов составляет его рост или снижение в отчетном периоде по сравнению с базисным периодом. Индекс цен Пааше характеризует, на сколько товары в отчетном периоде стали дороже либо дешевле, чем в базисном.
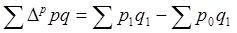При таком методе, рассчитав индекс цен, можно определить экономический эффект от изменения цен:
. (1.12)
Данная разность определяет абсолютную экономию (перерасход) денежных средств в результате изменения цен на товары.
До перехода к рыночным отношениям отечественная статистика отдавала предпочтение индексу цен Пааше. В условиях высокой инфляции взвешивание по весам отчетного периода (индекс Пааше) требует ежегодного (ежеквартального, ежемесячного) пересчета информации для формирования системы весов, что связано с большими временными и денежными затратами. Поэтому, начиная с 1991 года, органы государственной статистики России определяют изменения общего уровня цен на потребительские товары и услуги по формуле Ласпейреса, которой отдают предпочтение и в зарубежной статистике.
Американский экономист И. Фишер предложил «идеальный» индекс цен, так называемую идеальную форму индекса цен, который рассчитывается как средняя геометрическая из двух агрегатных индексов цен Ласпейреса и Пааше:
 |
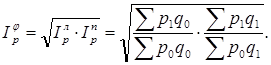(1.13)
Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный индекс представляет собой величину, обратную величине первоначального индекса. Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).
При синтезировании общего индекса цен вместо фактического количества товаров (в отчетном или базисном периоде) в качестве соизмерителей индексируемых величин могут применяться средние величины реализации товаров за два периода или более. При таком способе расчета формула общего индекса преобразуется и имеет вид:
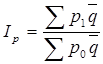, (1.14)
где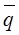 
- среднее значение количества товаров, реализованных за анализируемый период.
Рассчитанный по формуле (1.14) индекс принято называть индексом Лоу. Средняя величина физического объема продукции, используемая в качестве веса данного индекса, рассчитывается по формуле простой средней арифметической.
Индекс Лоу применяется в расчетах при закупках или реализации товара в течение продолжительных периодов времени. Этот метод дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
Встречаются и другие формулы расчета индексов. Так, итальянский ученый Р. Карли (1764 г.) вычислил общий индекс цен как среднюю арифметическую величину из частных индексов по формуле:
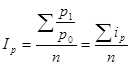. (1.15)
Из рассмотренных форм индексов цен наибольшее распространение в отечественной и зарубежной практике получили индексы Ласпейреса и Пааше. Значения этих индексов дают разные результаты. Это объясняется тем, что они имеют различный экономический смысл.
В табл. 1.1 представлены формулы построения агрегатных индексов.
Таблица 1.1 - Агрегатные индексы
| Название формул индексов | Формулы индексов | |
| индекс физического объема | индекс цен | |
| Индекс Ласпейреса (по базисным весам) |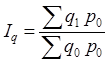 
| 
|
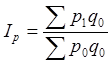
| Индекс Пааше (по отчетным весам) |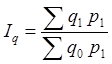 
| 
|
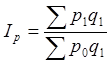
| Индекс Фишера |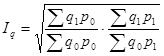 
| 
|
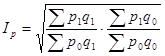
| Индекс Лоу (по средним весам) |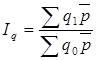 
| 
|
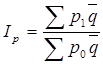
Индекс себестоимости характеризует среднее изменение себестоимости единицы продукции отчетного периода по сопоставимому с базисным периодом кругу продукции. Индекс себестоимости Пааше имеет вид:
 |
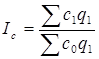, (1.16)
где ∑ c 1 q 1 - затраты на производство продукции отчетного периода;
∑ c 0 q 1 - 
затраты на производство продукции отчетного периода, если бы себестоимость оставалась на уровне базисного.
Индекс себестоимости Ласпейреса имеет вид:
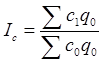, (1.17)
где 
∑ c 1 q 0 - затраты на производство продукции базисного периода, если бы себестоимость оставалась на уровне отчетного;
∑ c 0 q 0 - затраты на производство продукции базисного периода.
Абсолютная сумма изменения затрат за счет себестоимости рассчитывается по формуле: 
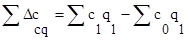(1.18)
Разность характеризует экономию (-) или перерасход (+) от снижения себестоимости единицы продукции.
Для характеристики уровня производительности труда используют два показателя: выработку (в натуральном и стоимостном выражении) и трудоемкость.
Выработка W – количество продукции, производимой в единицу рабочего времени (или на одного работника):
 |
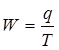, (1.19)
где W− средняя выработка;
q – количество произведённой продукции;
Т – затраты рабочего времени на производство продукции или численность работников.
Трудоемкость t – затраты труда на производство единицы продукции рассчитывается по формуле:
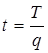. (1.20)
Трудоемкость – показатель, обратный производительности, т.е. чем выше трудоемкость, тем ниже производительность труда.
Индекс производительности труда, где в качестве индексируемой величины принимается трудоемкость продукции, по формуле Пааше имеет вид:
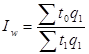
, (1.21)
 |
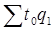где − условная величина, характеризующая затраты труда на продукцию отчетного периода при уровне производительности труда базисного периода;
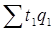− фактические затраты труда на продукцию отчетного периода.
Индекс производительности труда, где в качестве индексируемой величины принимается трудоемкость продукции, по формуле Ласпейреса имеет вид:
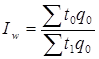
, (1.22)
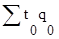
где − фактические затраты труда на продукцию базисного периода;
 |
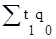− условная величина, характеризующая затраты труда на продукцию базисного периода при уровне производительности труда отчетного периода.
Абсолютный размер экономии времени (+) в связи с ростом производительности труда определяется следующим образом:
 |
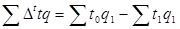. (1.23)
Индекс товарооборота определяется отношением стоимости продукции отчетного периода к стоимости продукции базисного периода:
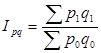. (1.24)
Этот индекс показывает, во сколько раз возросла (или уменьшилась) стоимость продукции отчетного периода по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости продукции. Если из индекса товарооборота вычесть 100%, то разность (Ipq–100) покажет, на сколько процентов изменилась стоимость продукции по сравнению с базисным периодом.
С помощью агрегатных индексов можно рассчитать абсолютный прирост результативного показателя по факторам:
 |
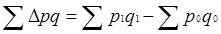. (1.25)
Разность показывает, на сколько денежных единиц изменилась стоимость продукции в текущем периоде по сравнению с базисным.
Значение индекса товарооборота зависит от двух факторов: изменения количества продукции (объема) и цен.
Пример. Рассчитать агрегатные индексы по данным табл. 1.2.
Таблица 1.2 - Выработка продукции
| Продукция, ед.изм. | Выработано продукции, тыс. | Цена за единицу, тыс. руб. |
| ||
| q0 | q1 | p0 | p1 | ||
| A, m | 500 | 500 | 15 | 16 | 1,00 |
| Б, m | 200 | 240 | 10 | 11 | 1,20 |
| B, m | 600 | 420 | 25 | 30 | 0,70 |
Индивидуальные индексы показывают, что в отчетном периоде выпуск продукции А оставался на уровне базисного периода i=1,0; продукции Б увеличился на 20%, а выпуск продукции В уменьшился на 30%.
Для определения изменения выпуска всей продукции рассчитаем общий индекс физического объема продукции:
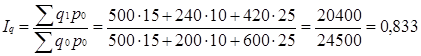
или 83,3% .
Физический объем всей продукции в отчетном периоде составляет 83,3% от его уровня в базисном периоде, он снизился за это время на 16,7% (0,833×100-100).
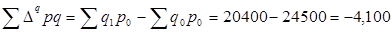Абсолютное снижение стоимости продукции в неизменных ценах, тыс. руб.:
,
т.е. –4,1 млн. руб.
Изменение общего объема продукции в фактических ценах (с учетом изменения цен) :
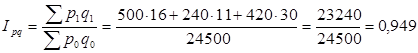
или 94,9%.
Общий выпуск снизился на 5,1% (94,9 - 100).
Дата: 2019-07-24, просмотров: 426.
