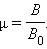В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ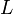 
, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz)[источник не указан 1017 дней]. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)[8]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года[источник не указан 1017 дней].
Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре:
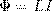(1)
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией.
Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
·c/А .
Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ0μ(N2I/l)S . Подставив в (1), найдем
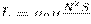(2)
т. е. индуктивность соленоида зависит от длины l солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида.
Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.
Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна
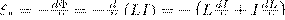
Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и
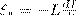(3)
где знак минус, определяемый правилом Ленца, говорит о том, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
Если ток со временем увеличивается, то (dI/dt<0) и ξs>0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs<0 т. е. индукционный ток имеет такое же направление, как и уменьшающийся ток в контуре, и замедляет его уменьшение. Значит, контур, обладая определенной индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока уменьшается тем сильнее, чем больше индуктивность контура.
42. Ток при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с.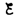 
, резистор сопротивлением R и катушку индуктивностью L . Под действием внешней э. д. с. в цепи течет постоянный ток
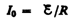
(внутренним сопротивлением источника тока пренебрегаем).
В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции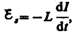 
препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I= 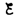s / R , или
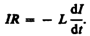(127.1)
Разделив в выражении (127.1) переменные, получим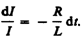 
Интегрируя это уравнение по I (от I0 до I) и t (от 0 до t), находим ln (I /I0) = – Rt / L , или
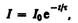(127.2)
где t=L / R — постоянная, называемая временем релаксации. Из (127.2) следует, что t есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше t и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При замыкании цепи помимо внешней э. д. с. 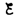возникает э. д. с. самоиндукции 
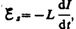препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома, 
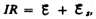или
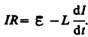
Введя новую переменную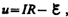 
преобразуем это уравнение к виду
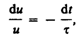
где t — время релаксации.
В момент замыкания (t=0) сила тока I = 0 и u = – 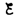. Следовательно, интегрируя по и (от – 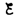до IR – 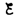) и t (от 0 до t), находим ln[(IR – 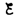)]/– 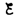= — t / t , или
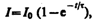(127.3)
где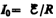 
— установившийся ток (при t®¥).
Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I =0 и асимптотически стремится к установившемуся значению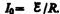 
. Скорость нарастания тока определяется тем же временем релаксации t = L / R , что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.
Оценим значение э.д.с. самоиндукции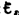 
, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R0 до R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток 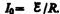. При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение дляI0 и t, получим
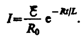
Э.д.с. самоиндукции
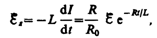
т. е. при значительном увеличении сопротивления цепи ( R / R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
43. Явление взаимной индукции. Трансформатор.
Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I1, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I1. Обозначим через Ф21 часть потока,пронизывающая контур 2. Тогда
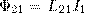(1)
где L21 — коэффициент пропорциональности.
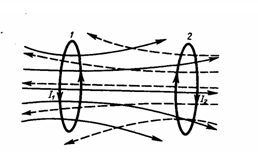
Рис.1
Если ток I1 меняет свое значение, то в контуре 2 индуцируется э.д.с. ξi2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф21, который создается током в первом контуре и пронизыващет второй:
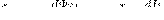
Аналогичным образом, при протекании в контуре 2 тока I2 магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф12 — часть этого потока, который пронизывает контур 1, то
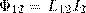
Если ток I2 меняет свое значение, то в контуре 1 индуцируется э.д.с. ξi1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф12, который создается током во втором контуре и пронизывает первый:
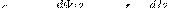
Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L21 и L12 называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L21 и L12 равны друг другу, т. е.
(2)
Коэффициенты пропорциональности L12 и L21 зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн).
Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N1, током I1 и магнитной проницаемостью μ сердечника, B = μμ0(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ0(N1I1/l)S
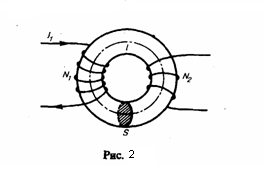
Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N2 витков,
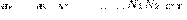
Поток Ψ создается током I1, поэтому, используя (1), найдем
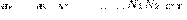(3)
Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L12 получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,
Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока
Закон Фарадея
См. также: Электромагнитная индукция
ЭДС, создаваемая во вторичной обмотке, может быть вычислена по закону Фарадея, который гласит, что:
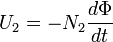
Где
U2 — Напряжение на вторичной обмотке,
N2 — число витков во вторичной обмотке,
Φ — суммарный магнитный поток, через один виток обмотки. Если витки обмотки расположены перпендикулярно линиям магнитного поля, то поток будет пропорционален магнитному полю B и площади S через которую он проходит.
ЭДС, создаваемая в первичной обмотке, соответственно:
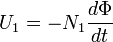
Где
U1 — мгновенное значение напряжения на концах первичной обмотки,
N1 — число витков в первичной обмотке.
Поделив уравнение U2 на U1, получим отношение[6]:
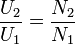
44. Энергия магнитного поля, её плотность.
Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.
Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна
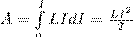
Значит, энергия магнитного поля, которое связано с контуром,
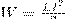(1)
Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем
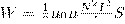
Так как I=Bl/(μ0μN) и В=μ0μH , то
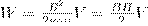(2)
где Sl = V — объем соленоида.
Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью
(3)
Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.
45. Магнитное поле в веществе. Намагниченность. Магнитная проницаемость. Напряженность магнитного поля, её связь с магнитной индукцией.
Магнитное поле в веществе
Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.
Физическая величина, показывающая, во сколько раз индукция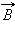 
магнитного поля в однородной среде отличается по модулю от индукции 
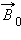магнитного поля в вакууме, называется магнитной проницаемостью:
|
Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.
Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.
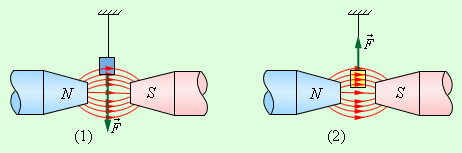
Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10–5, у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10–6), вода (μ – 1 ≈ –9·10–6), висмут (μ – 1 ≈ –1,7·10–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).
|
| Рисунок 1.19.1. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле |
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.
В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.
Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.
Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 102–105. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.
К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.
Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.
Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.
Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).
Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовленияпостоянных магнитов.
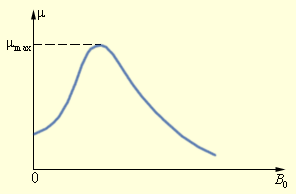
Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B0 внешнего поля. Типичная зависимость μ (B0) приведена на рис. 1.19.2. В таблицах обычно приводятся значения максимальной магнитной проницаемости.
|
| Рисунок 1.19.2. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля |
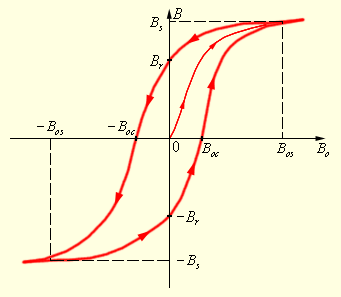
Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B0внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B0) ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 1.19.3).
|
| Рисунок 1.19.3. Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B0 внешнего магнитного поля |
Из рис. 1.19.3 видно, что при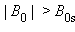 
наступает магнитное насыщение – намагниченность образца достигает максимального значения.
Если теперь уменьшать магнитную индукцию B0 внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно Br. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B0 до значения –B0c, которое принято называтькоэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 1.19.3.
У магнито-мягких материалов значения коэрцитивной силы B0c невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.
Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10–2–10–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.
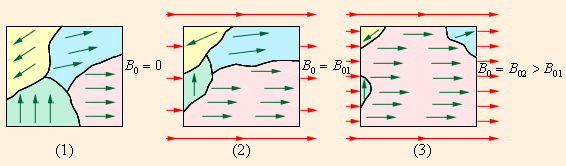
В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля 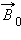происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. 1.19.4 может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.
|
| Рисунок 1.19.4. Намагничивание ферромагнитного образца. (1) B0 = 0; (2) B0 = B01; (3) B0 = B02 > B01 |
Дата: 2019-07-24, просмотров: 239.
