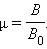Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной.

 ( ... но, не числа заряженных частиц, т.к. существуют превращения элементарных частиц).

Замкнутая система

- система частиц, в которую не входят извне и не выходят наружу заряженные частицы.

Закон Кулона

- основной закон электростатики.

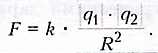
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна

 произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.

 

 Когда тела считаются точечными? - если расстояние между ними во много раз больше размеров тел.

 Если у двух тел есть электрические заряды, то они взаимодействуют по закону Кулона.

1. Напряженность электрического поля. Принцип суперпозиции. Расчёт электростатического поля системы точеных зарядов на основе принципа суперпозиции.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 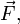 действующей на неподвижный[ пробный заряд, помещенный в данную точку поля, к величине этого заряда  :

.

 

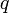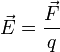
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

 

 

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

 

 

3.

Линии напряжонности (силовые линии) электрического поля. Поток вектора напряжонности. Густота силовых линий.

Электрическое поле изображают с помощью силовых линий.

Силовые линии указывают направление силы, действующей на положительный заряд в данной точке поля.

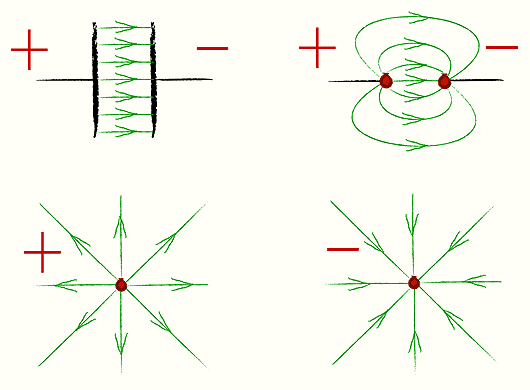
Свойства силовых линий электрического поля

· Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных.

· Силовые линии электрического поля всегда перпендикулярны поверхности проводника.

· Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным(если силовые линии параллельны) и неоднородным (если силовые линии не параллельны).

Силовые линии электрического поля

стр. 448

Основные понятия.

 

Сила тока - скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

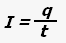
где I - сила тока, q - величина заряда (количество электричества), t - время прохождения заряда.

Плотность тока - векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

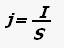
где j -плотность тока, S - площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение - скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

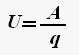
где A - полная работа сторонних и кулоновских сил, q - электрический заряд.

Электрическое сопротивление - физическая величина, характеризующая электрические свойства участка цепи.

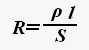
где ρ - удельное сопротивление проводника, l - длина участка проводника, S - площадь поперечного сечения проводника.

 

Проводимостью называется величина, обратная сопротивлению

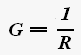
где G - проводимость.

 

 

Законы Ома.

 

Параллельное соединение

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках: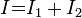

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: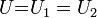

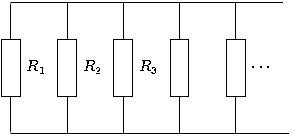
[править]Резистор

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 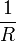складывается из проводимостей каждого резистора )

 

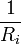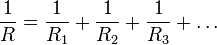
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему^[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиямиимпеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

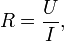
где

R — сопротивление;

U — разность электрических потенциалов на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

 

Электри́ческая проводи́мость (электропроводность, проводимость) — способность тела проводить электрический ток, а такжефизическая величина, характеризующая эту способность и обратная электрическому сопротивлению. В СИ единицей измеренияэлектрической проводимости является сименс (называемая также в некоторых странах Мо)^[1].

Удельной проводимостью (удельной электропроводностью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего токаи величиной электрического поля в среде:

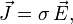
где

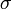§ — удельная проводимость,

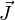§ — вектор плотности тока,

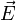§ — вектор напряжённости электрического поля.

 

19. ЭДС, разность потенциалов и напряжение.

 

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил ( 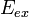). В замкнутом контуре ( 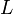) тогда ЭДС будет равна:

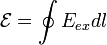, где 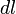— элемент длины контура.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

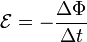
где 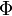— поток магнитного поля через замкнутую поверхность 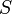, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

 

Электрическое напряжение между двумя точками электрической цепи или электрического поля, равно работе электрического поля по перемещению единичного положительного заряда из одной точки в другую. В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд; в этом случае Э. н. между двумя точками совпадает с разностью потенциалов между ними.

Если поле непотенциально, то напряжение зависит от того пути, по которому перемещается заряд между точками. Непотенциальные силы, называются сторонними, действуют внутри любого источника постоянного тока (генератора, аккумулятора, гальванического элемента и др.). Под напряжением на зажимах источника тока всегда понимают работу электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника; в этом случае Э. н. равно разности потенциалов на зажимах источника и определяется законом Ома: U = IR—E, где I — сила тока, R — внутреннее сопротивление источника, а E — его электродвижущая сила (эдс). При разомкнутой цепи (I = 0) напряжение по модулю равно эдс источника. Поэтому эдс источника часто определяют как Э. н. на его зажимах при разомкнутой цепи.

В случае переменного тока Э. н. обычно характеризуется действующим (эффективным) значением, которое представляет собой среднеквадратичное за период значение напряжения. Напряжение на зажимах источника переменного тока или катушки индуктивности измеряется работой электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника или катушки. Вихревое (непотенциальное) электрическое поле на этом пути практически отсутствует, и напряжение равно разности потенциалов.

Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

Наименование и обозначение производной единицы СИ:

международное – volt, V

русское – вольт, В

Выражение через основные и производные единицы СИ:

1 V = 1 W / A

 

20. Закон Джоуля-Ленца (интегральная и дифференциальная формы).

Принцип суперпозиции

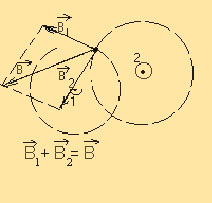
Для магнитного поля, как и для электрического поля, справедлив принцип суперпозиции: поле 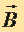, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей 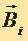, порождаемых каждым зарядом (током) в отдельности: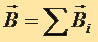

т.е., чтобы найти силу, действующую на точку в пространстве, нужно сложить силы, действующие на неё, как показано на рисунке

Магнитное поле кругового тока представляет собой некую восьмёрку с разделением колец в центре кольца, по которому течёт ток. Его схема показана на рисунке

 

 

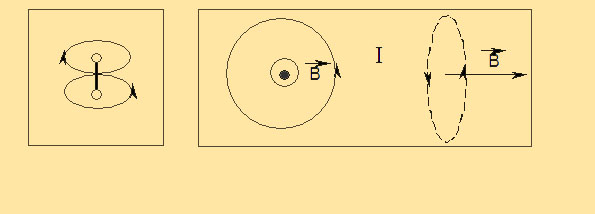
28. Сила Лоренца. Движение заряженных частиц в магнитом поле.

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженнуючастицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью 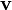заряд 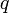лишь со сторонымагнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороныэлектрического 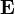и магнитного 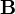полей. Выражается в СИ как:

 

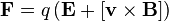
Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.

Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv²/r , следовательно

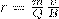(1)

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

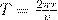
Подствавив (1), получим

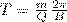(2)

т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц.

В случае, если скорость v заряженной частицы направлена под углом α к вектору В (рис. 170), то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью v_parall=vcosα ; 2) равномерного движения со скоростью v_perpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить v_perpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии

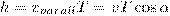
Подставив в данное выражение (2), найдем

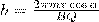
Направление, в котором закручивается спираль, определяется знаком заряда частицы.

Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.

 

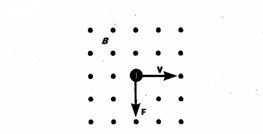
Рис.1

 

 

29. Эффект Холла и его применение.

 

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 годув тонких пластинках золота.

 

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле 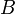течёт электрический ток под действием напряжённости 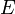. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

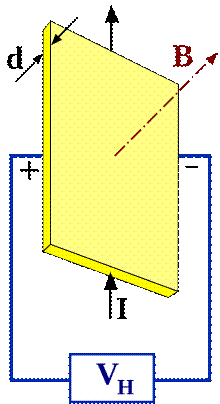
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов 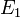не скомпенсирует магнитную составляющую силы Лоренца:

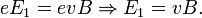
Скорость электронов 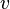можно выразить через плотность тока:

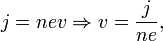
где 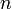— концентрация носителей заряда. Тогда

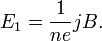
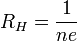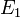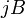Коэффициент пропорциональности между и называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак 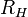, что объясняется в полуклассической и квантовой теориях твёрдого тела.

 

Аномальный эффект Холла

Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.

Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью^[2].

[править]Квантовый эффект Холла

Основная статья: Квантовый эффект Холла

В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.

[править]Спиновый эффект Холла

Основная статья: Спиновый эффект Холла

В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.

 

 

Применение

Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.

Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле илиполупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников.

На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в коллекторном ДПТ.

Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей.

 

 

30. Закон Био-Савара-Лапласа

Магнитное поле постоянных токов различной формы исследовалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты их опытов были обобщены французским ученым П. Лапласом.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен

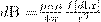(1)

где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.

Модуль вектора dB задается выражением

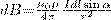(2)

где α — угол между векторами dl и r.

Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

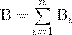(3)

Используя данные формулы для расчет характеристик магнитного поля (В и Н) в общем случае достаточно сложен. Однако если распределение тока имеет какую-либо симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции дает возможность просто рассчитать некоторые поля. Рассмотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому бесконечному проводу (рис. 2).

 

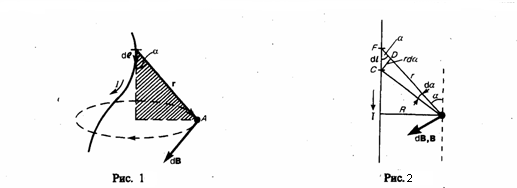
В произвольной точке А, удаленной на расстояние R от оси проводника, векторы dB от всех элементов тока имеют одинаковое направление, которое перпендикулярно плоскости чертежа («к вам»). Значит, сложение всех векторов dB можно заменить сложением их модулей. За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины. Из рис. 2 следует, что

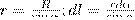
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти формулы в (2), получим, что магнитная индукция, которая создавается одним элементом проводника, равна

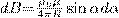(4)

Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то, согласно (3) и (4),

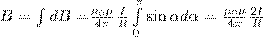
Значит, магнитная индукция поля прямого тока

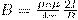(5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как видно из рисунка, каждый элемент кругового проводника с током создает в центре магнитное поле одинакового направления - вдоль нормали от витка. Значит, сложение векторов dB также можно заменить сложением их модулей. Поскольку расстояние всех элементов проводника до центра кругового тока одинаково и равно R и все элементы проводника перпендикулярны радиусу-вектору (sinα=1), то, используя (2),

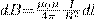
Тогда

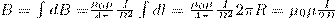
Следовательно, магнитная индукция поля в центре кругового проводника с током

 

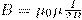
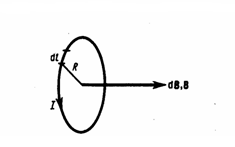
Рис.3

 

 

31. Закон Био-Савара-Лапласа и применение его к расчёту магнитного поля прямолинейного проводника стоком.

 

 

В произвольной точке А, удаленной на расстояние R от оси проводника, векторы dB от всех элементов тока имеют одинаковое направление, которое перпендикулярно плоскости чертежа («к вам»). Значит, сложение всех векторов dB можно заменить сложением их модулей. За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины. Из рис. 2 следует, что

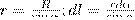
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти формулы в (2), получим, что магнитная индукция, которая создавается одним элементом проводника, равна

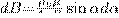(4)

Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то, согласно (3) и (4),

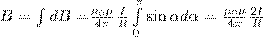
Значит, магнитная индукция поля прямого тока

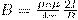(5)

 

32. Закон Био-Савара-Лапласа и применение его к расчёту магнитного поля оси кругового витка с током

 

Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

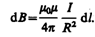
Тогда

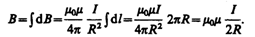
Следовательно, магнитная индукция поля в центре кругового проводника с током

 

 

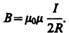
33. Магнитное поле движущегося заряда. Взаимодействие параллельных проводников с током.

 

Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q , свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой

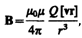(113.1)

где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в кото­рой расположены векторы v и r, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

Модуль магнитной индукции (113.1) вычисляется по формуле

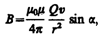(113.2)

где a — угол между векторами v и r.

Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:

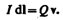
Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.

Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на — Q . Скорость v — относительная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный харак­тер магнитного поля движущегося заряда.

Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Мо­сковского университета А. А. Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академи­ком А. Ф. Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.

Если близко один к другому расположены проводники с токами одного направления, то магнитные линии этих проводников, охва­тывающие оба проводника, обладая свойством продольного натяже­ния и стремясь сократиться, будут заставлять проводники притя­гиваться (рис. 90, а).

Магнитные линии двух проводников с токами разных направле­ний в пространстве между проводниками направлены в одну сто­рону. Магнитные линии, имеющие одинаковое направление, будут взаимно отталкиваться. Поэтому проводники с токами противопо­ложного направления отталкиваются один от другого (рис. 90, б).

 

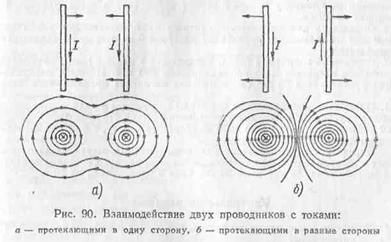
Рассмотрим взаимодействие двух параллельных проводников с токами, расположенными на расстоянии а один от другого. Пусть длина проводников равна l.

Магнитная индукция, созданная током I₁ на линии расположе­ния второго проводника, равна

 

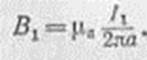
На второй проводник будет действовать электромагнитная сила

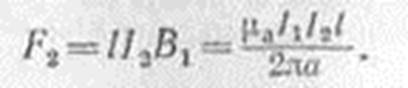
Магнитная индукция, созданная током I₂ на линии расположе­ния первого проводника, будет равна

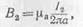
и на первый проводник действует электромагнитная сила

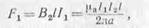
равная по величине силе F2

 

На электромеханическом взаимодействии проводников с токо^ основан принцип действия электродинамических измерительных прИб&ров; используемых в цепях постоянного и в особенности пере­менного тока.

 

 

34. Закон полного тока и применение его к расчёту магнитных полей длинного соленоида и тороида

 

Закон полного тока

Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.

Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.

Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.

На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.

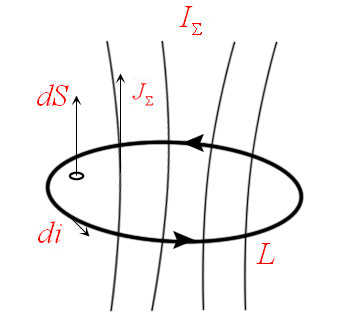
Далее представим то, что поверхность S пронизывается отдельной системой токов, которая может нести как дискретный характер (к примеру, систему отдельных проводников), так и быть непрерывно распределенной (электронный поток может послужить этому примером). Не обуславливая тем временем физической природы данных токов, будем подразумевать для конкретности, что они распределены непрерывно в пространстве с кое-какой плотностью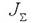

То теперь полный ток, пронизывающий контур, найдется в виде

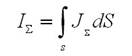
Закон полного тока говорит о том, что циркуляция по контуру L вектора напряженности магнитного поля, инициированного протеканием тока 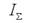равна полному току, то есть.

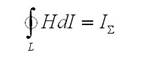
Закон полного тока формулирует соотношение выше в интегральной форме.

В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство

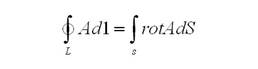
Использовав крайнюю формулу и перестроив с её помощью

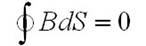
будем располагать

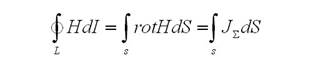
откуда получим из-за произвольности выбранного контура

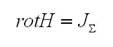
Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.

Ток смещения

Известен из практики факт прохождения электрического переменного тока по цепи, включающий в себя конденсатор. Значительно важным тут приходится то, что ток протекает между обкладками по пространству, в котором нет каких-либо носителей электрического заряда. Вследствие чего можно предположить, что в данной области течёт некий ток, натура которого принципиально непохожа на натуры тока проводимости, ранее освоенного. Данный ток впервые был влит в электродинамику Максвеллом, а назвал он его током смещения.

Мы видим цепь с конденсатором, представленную изображением ниже, в нём выделена замкнутая поверхность S, охватывающая одну из обкладок конденсатора.

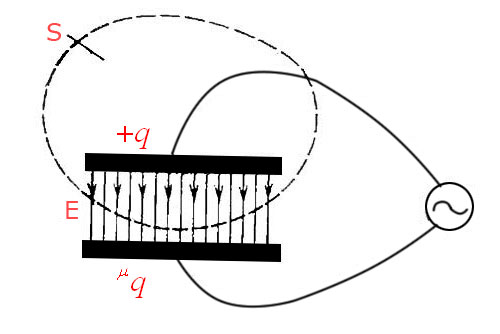
Из закона Гаусса надлежит, что если, когда между обкладками имеется вакуум,

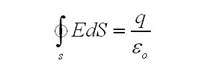
Ток в цепи в свою очередь, найдется следующим образом:

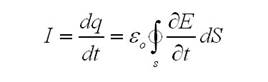
Последнее выражение показывает, что величина

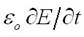
обладает размерностью плотности тока, который и должен называться током смещения.

Таким образом, плотность тока смещения в вакууме

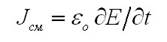
Предложением Максвелла было введение плотности тока смещения в правую часть закона полного тока наряду плотностью тока проводимости. Данное решение оказалось довольно значительным для электродинамики, поскольку при этом становилось возможным устанавить внутреннюю взаимосвязь магнитного и электрического поля. В действительности, к протеканию тока смещения, который, в свою очередь, вызывает появление магнитного поля, приводит изменение во времени электрического поля в какой-либо точке пространства.

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA , как показано на рис. 175. Циркуляция вектора В по замкнутому контуру ABCDA , охватывающему все N витков, согласно (118.1), равна

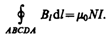
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA . На участках АВ и CD контур перпендикулярен линиям магнитной индукции и B_l =0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна В l (контур совпадает с линией магнитной индукции); следовательно,

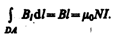(119.1)

Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

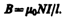(119.2)

Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био - Савара - Лапласа; в результате получается та же формула (119.2).

Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

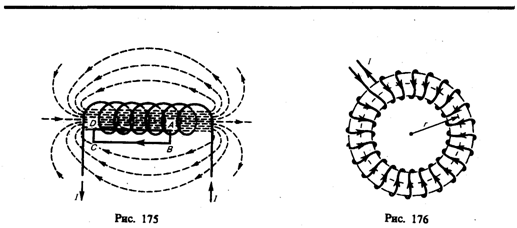
Линии магнитной индукции в данном случае, как следует из соображений симмет­рии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118.1), B ×2pr = m₀NI , откуда следует, что магнитная индукция внутри тороида (в вакууме)

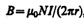
где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B ×2pr =0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).

 

 

35. Поток вектора магнитной индукции, его единица СИ. Теорема Гаусса для магнитного поля.

 

Магни́тный пото́к — поток 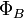как интеграл вектора магнитной индукции 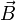через конечную поверхность 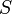. Определяется через интеграл по поверхности

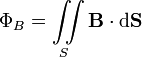
при этом векторный элемент площади поверхности определяется как

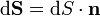
где 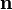— единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

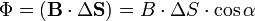
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

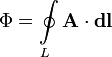
В СИ единицей магнитного потока является Вебер (Вб, размерность — В·с = кг·м²·с⁻²·А⁻¹),

в системе СГС — максвелл (Мкс); 1 Вб = 10⁸ Мкс.

 

 

Рис.1

 

Исследуя результаты своих многочисленных опытов, Фарадей пришел к заключению, что индукционный ток возникает всегда, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также появляется индукционный ток - в этом случае индукция магнитного поля вблизи контура остается постоянной, а меняется только поток магнитной индукции сквозь контур.

В результате опыта было также установлено, что значение индукционного тока абсолютно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (также в опытах Фарадея доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения магнита, или скорость изменения силы тока, или скорость движения катушек).

Открытие явления электромагнитной индукции имело огромное значение, поскольку была дана возможность получения электрического тока с помощью магнитного поля. Этим оьткрытие дало взаимосвязь между электрическими и магнитными явлениями, что в дальнейшем послужило толчком для разработки теории электромагнитного поля.

 

 

38. Вывод ЭДС индукции из закона сохранения энергии. Механизм возникновения ЭДС индукции. Вихревые токи (Токи Фуко)

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электро­магнитной индукции 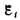определяются только скоростью изменения магнитного потока, т. е.

 

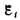
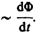
Теперь необходимо выяснить знак 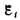. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.

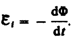(123.2)

Знак минус показывает, что увеличение потока 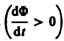вызывает э. д. с. 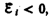т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока 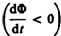вызывает 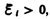т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

Механизм возникновения э.д.с. индукции можно пояснить на простом примере. Пусть изменение магнитного потока, пронизывающего контур, проис-ходит за счет изменения площади контура вследствие движения одного из проводников, составляющих контур. Пусть, например, контур образован п-образным проводником 1 и скользящей перемычкой 2 (рис. 3.12), и пусть линии индукции магнитного поля В перпендикулярны плоскости контура и направлены от нас (показаны крестиками).

 

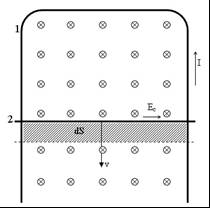
Рис. 3.12

 

При скольжении перемычки вниз площадь контура S будет возрастать, что приведет к возрастанию магнитного потока, равного ВS. При этом, со-гласно закону Фарадея должна возникнуть э.д.с. индукции. Непосредственной физической причиной возникновения индукционного тока в контуре в данном случае является сила Лоренца. Действительно, при движении перемычки вниз со скоростью v, с той же скоростью будут перемещаться находящиеся в ней электроны. Сила Лоренца, действующая на каждый электрон, будет равна evB (где е - заряд электрона) и направлена влево. Формально эту силу можно рассматривать как проявление поля сторонних сил, имеющего напряженность Е_с. Из формулы (2.22) вытекает, что Е_с = vB. Электродвижущая сила индукции Е_i, создаваемая полем Е_сво всей движущейся перемычке длиной l будет согласно (2.24) равна

Е_i = òЕ_сldl = Е_сl = vBl . (3.25)

Скорость v движения перемычки представим как производную dx/dt. Тогда

Е_i 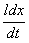= В = В 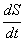(3.26)

В (3.26) учтено, что произведение ldx представляет со-бой приращение dS площади контура. В свою очередь произведение BdS равно приращению dФ магнитного потока. В итоге мы получаем, что э.д.с. индукции равна производной dФ/dt от магнитного потока

Е_i = dФ/dt, (3.27)

то есть мы пришли к закону Фарадея. В проведенных рассуждениях мы для простоты оперировали модулями векторов Е_с, v и В, поэтому ве-личину э.д.с. индукции в формуле (3.27) определили также лишь по модулю.

Рассмотренное объяснение механизма возникновения э.д.с. индукции относится к случаю, когда изменение магнитного потока происходит за счет подвижных проводников. Но магнитный поток может меняться также и путем изменения величины В при неизменной геометрии контура. Тогда сила Лоренца не возникает, а ин-дукционный ток возбуждается в этом случае вихревым электрическим полем, порождае-мым меняющимся во времени магнитным полем. Этот более общий случай возникновения э.д.с. индукции будет рассмотрен в следующем разделе (тема 4).

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.

Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и др.

Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.

 

39. Вращение проводящей рамки в магнитном поле. Баллистический способ измерения магнитной индукции.

 

 

Явление электромагнитной индукции часто используется для преобразования механической энергии в энергию электрического тока. Для этой цели применяются генераторы, принцип действия которых рассмотрим на примере плоской рамки, которая вращается в однородном магнитном поле.

 

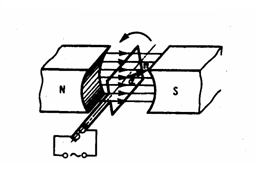
Рис.1

 

Пусть рамка вращается в однородном магнитном поле (B=const) равномерно с угловой скоростью ω=const. Магнитный поток, который сцеплен с рамкой площадью S, в любой произвольный момент времени t будет равен

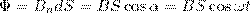
где α = ωt — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t=0 было α=0).

Во время вращения рамки в ней будет появляться переменная э.д.с. индукции

(1)

которая изменяется со временем по гармоническому закону. При sinαt = 1 э.д.с. ξ_i максимальна, т. е.

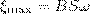(2)

Учитывая (2), формула (1) запишется как

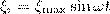
Значит, если рамка вращается равномерно в однородном магнитном поле, то в ней возникает переменная э.д.с., которая изменяется по гармоническому закону.

Из формулы (2) следует, что ξ_max (следовательно, и э.д.с. индукции) находится в непосредственной зависимости от величин ω, B и S. В России принята стандартная частота тока ν = ω/(2π) = 50 Гц, поэтому на практике возможно лишь увеличение двух остальных величии. Для увеличения В применяют мощные постоянные магниты или пропускают значительный ток в электромагнитах, а также внутрь электромагнита помещают сердечники из материалов с большим значением магнитной проницаемостью μ. Если вращать не один, а большое количество витков, соединенных последовательно, то тем самым увеличивается S. Переменное напряжение снимается с вращающегося витка с помощью щеток, схематически изображенных на рис. 1.

Процесс превращения механической энергии в электрическую обратим. Если по рамке, которая помещена в магнитное поле, пропускать электрический ток, то в магнитном поле на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателей, имеющих предназначение превращать электрическую энергии в механическую.

 

Баллистический метод основан на измерении баллистическим гальванометром количества электричества, индуктируемого в измерительной катушке при быстром изменении сцепленного с ней магнитного потока (см. Баллистический метод электроизмерений). Кроме баллистических гальванометров, для измерения магнитного потока применяют веберметры (флюксметры) - магнитоэлектрические и фотоэлектрические. Веберметрами можно измерять медленно меняющиеся потоки. Баллистическим методом определяют основную кривую индукции В (Н), кривую намагничивания J (H), петлю гистерезиса, различные виды проницаемости и размагничивающий фактор ферромагнитных образцов.

 

 

40. Явление самоиндукции. ЭДС самоиндукции.

 

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре^[1] при изменении тока, протекающего по контуру.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока :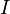

.

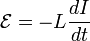Коэффициент пропорциональности 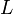называется коэффициентом самоиндукции или индуктивностью контура (катушки).

 

ЭДС индукции

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

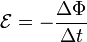
где 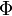— поток магнитного поля через замкнутую поверхность 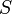, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

 

 

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

 

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

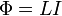
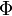— магнитный поток, 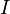— ток в контуре, 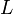— индуктивность.

§ Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

.

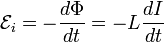Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током^[4]:

.

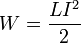Рис.1

 

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй:

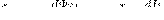
Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то

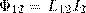
Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый:

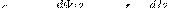
Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е.

(2)

Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн).

Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ₀(N₁I₁/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф₂ = BS = μμ₀(N₁I₁/l)S

 

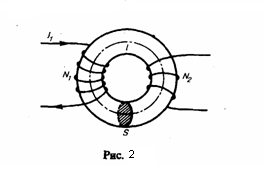
Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков,

Поток Ψ создается током I₁, поэтому, используя (1), найдем

(3)

Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,

 

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Закон Фарадея

См. также: Электромагнитная индукция

ЭДС, создаваемая во вторичной обмотке, может быть вычислена по закону Фарадея, который гласит, что:

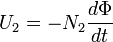
Где

U₂ — Напряжение на вторичной обмотке,

N₂ — число витков во вторичной обмотке,

Φ — суммарный магнитный поток, через один виток обмотки. Если витки обмотки расположены перпендикулярно линиям магнитного поля, то поток будет пропорционален магнитному полю B и площади S через которую он проходит.

ЭДС, создаваемая в первичной обмотке, соответственно:

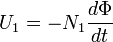
Где

U₁ — мгновенное значение напряжения на концах первичной обмотки,

N₁ — число витков в первичной обмотке.

Поделив уравнение U₂ на U₁, получим отношение^[6]:

 

 

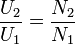
44. Энергия магнитного поля, её плотность.

 

 

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна

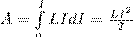
Значит, энергия магнитного поля, которое связано с контуром,

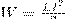(1)

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем

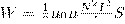
Так как I=Bl/(μ₀μN) и В=μ₀μH , то

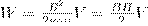(2)

где Sl = V — объем соленоида.

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью

(3)

Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.

 

45. Магнитное поле в веществе. Намагниченность. Магнитная проницаемость. Напряженность магнитного поля, её связь с магнитной индукцией.

 

Магнитное поле в веществе

Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.

Физическая величина, показывающая, во сколько раз индукция 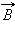магнитного поля в однородной среде отличается по модулю от индукции 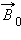магнитного поля в вакууме, называется магнитной проницаемостью:

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.

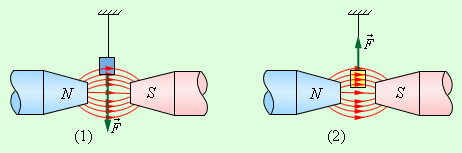
Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).

Рисунок 1.19.1. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле

Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.

В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.

Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.

Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 10²–10⁵. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.

К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.

Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.

Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.

Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).

Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовленияпостоянных магнитов.

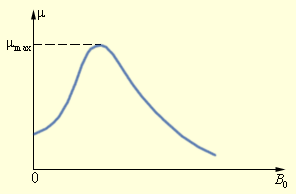
Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B₀ внешнего поля. Типичная зависимость μ (B₀) приведена на рис. 1.19.2. В таблицах обычно приводятся значения максимальной магнитной проницаемости.

Рисунок 1.19.2. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля

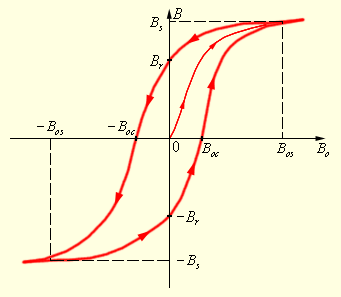
Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B₀внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B₀) ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 1.19.3).

Рисунок 1.19.3. Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B0 внешнего магнитного поля

Из рис. 1.19.3 видно, что при 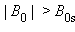наступает магнитное насыщение – намагниченность образца достигает максимального значения.

Если теперь уменьшать магнитную индукцию B₀ внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно B_r. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B₀ до значения –B_0c, которое принято называтькоэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 1.19.3.

У магнито-мягких материалов значения коэрцитивной силы B_0c невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.

Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10^–2–10^–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.

В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля 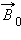происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. 1.19.4 может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.

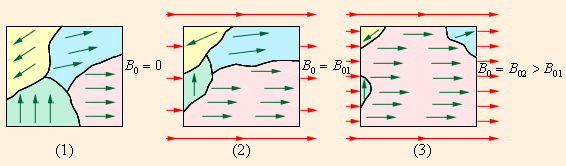
Рисунок 1.19.4. Намагничивание ферромагнитного образца. (1) B0 = 0; (2) B0 = B01; (3) B0 = B02 > B01

 

 

В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной.

 ( ... но, не числа заряженных частиц, т.к. существуют превращения элементарных частиц).

Замкнутая система

- система частиц, в которую не входят извне и не выходят наружу заряженные частицы.

Закон Кулона

- основной закон электростатики.

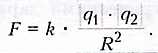
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна

 произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.

 

 Когда тела считаются точечными? - если расстояние между ними во много раз больше размеров тел.

 Если у двух тел есть электрические заряды, то они взаимодействуют по закону Кулона.

1. Напряженность электрического поля. Принцип суперпозиции. Расчёт электростатического поля системы точеных зарядов на основе принципа суперпозиции.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 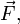 действующей на неподвижный[ пробный заряд, помещенный в данную точку поля, к величине этого заряда  :

.

 

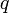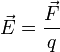
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

 

 

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

 

 

3.