Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
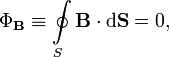
или в дифференциальной форме
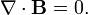
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.
36. Работа по перемещению проводника и контура с током в магнитном поле.
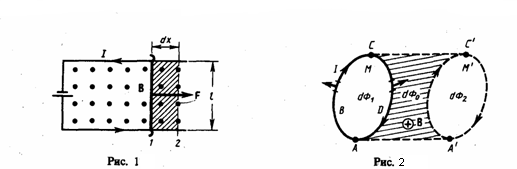
На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.
Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле
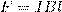
Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна
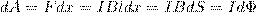
так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,
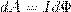(1)
т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.
Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.
Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е.
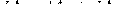(2)
Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA2>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, который пронизывает контур в его конечном положении. Значит,
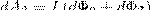(3)
Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA1<0. Проводник AВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,
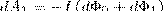(4)
Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:
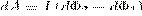
где dФ2—dФ1=dФ' — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,
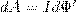(5)
Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:
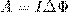(6)
значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле.
37. Явление электромагнитной индукции (опыты Фарадея). Закон электромагнитной индукции. Правило Ленца
Правило Ленца определяет направление индукционного тока и гласит:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока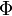 
, пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением[1]:
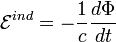
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работытрансформаторов, дросселей, многих видов электродвигателей и генераторов.[1] Закон гласит:
Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.[1]
или другими словами:
Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.
Как известно, электрические токи порождают вокруг себя магнитное поле. Связь магнитного поля с током дала толчок к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальное открытие было блестяще сделано в 1831 г. английским физиком М. Фарадеем, который открыл явленение электромагнитной индукции. Оно говорит о том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.
Приведем классические опыты Фарадея, с помощью которых было открыто явление электромагнитной индукции.
Опыт I (рис. 1а). Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.
Опыт II. Концы одной из катушек, которая вставлена одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. В моменты включения или выключения тока наблюдается отклонение стрелки гальванометра, а также в моменты его уменьшения или увеличения, а также при перемещении катушек друг относительно друга (рис. 1б). Направления отклонений стрелки гальванометра также имею противоположные направления при включении или выключении тока, его увеличении или уменьшении, приближении или удалении катушек.
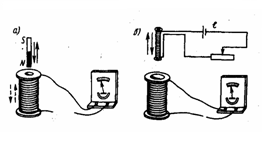
Рис.1
Исследуя результаты своих многочисленных опытов, Фарадей пришел к заключению, что индукционный ток возникает всегда, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также появляется индукционный ток - в этом случае индукция магнитного поля вблизи контура остается постоянной, а меняется только поток магнитной индукции сквозь контур.
В результате опыта было также установлено, что значение индукционного тока абсолютно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (также в опытах Фарадея доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения магнита, или скорость изменения силы тока, или скорость движения катушек).
Открытие явления электромагнитной индукции имело огромное значение, поскольку была дана возможность получения электрического тока с помощью магнитного поля. Этим оьткрытие дало взаимосвязь между электрическими и магнитными явлениями, что в дальнейшем послужило толчком для разработки теории электромагнитного поля.
38. Вывод ЭДС индукции из закона сохранения энергии. Механизм возникновения ЭДС индукции. Вихревые токи (Токи Фуко)
Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электромагнитной индукции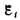 
определяются только скоростью изменения магнитного потока, т. е.
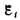
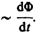
Теперь необходимо выяснить знак 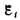. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.
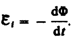(123.2)
Знак минус показывает, что увеличение потока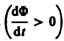 
вызывает э. д. с. 
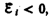т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока 
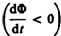вызывает 
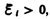т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) определяется правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.
Механизм возникновения э.д.с. индукции можно пояснить на простом примере. Пусть изменение магнитного потока, пронизывающего контур, проис-ходит за счет изменения площади контура вследствие движения одного из проводников, составляющих контур. Пусть, например, контур образован п-образным проводником 1 и скользящей перемычкой 2 (рис. 3.12), и пусть линии индукции магнитного поля В перпендикулярны плоскости контура и направлены от нас (показаны крестиками).
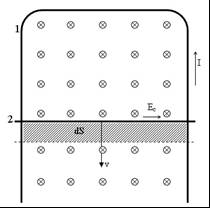
Рис. 3.12
При скольжении перемычки вниз площадь контура S будет возрастать, что приведет к возрастанию магнитного потока, равного ВS. При этом, со-гласно закону Фарадея должна возникнуть э.д.с. индукции. Непосредственной физической причиной возникновения индукционного тока в контуре в данном случае является сила Лоренца. Действительно, при движении перемычки вниз со скоростью v, с той же скоростью будут перемещаться находящиеся в ней электроны. Сила Лоренца, действующая на каждый электрон, будет равна evB (где е - заряд электрона) и направлена влево. Формально эту силу можно рассматривать как проявление поля сторонних сил, имеющего напряженность Ес. Из формулы (2.22) вытекает, что Ес = vB. Электродвижущая сила индукции Еi, создаваемая полем Есво всей движущейся перемычке длиной l будет согласно (2.24) равна
Еi = òЕсldl = Есl = vBl . (3.25)
Скорость v движения перемычки представим как производную dx/dt. Тогда
Еi 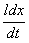= В 
= В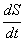 
(3.26)
В (3.26) учтено, что произведение ldx представляет со-бой приращение dS площади контура. В свою очередь произведение BdS равно приращению dФ магнитного потока. В итоге мы получаем, что э.д.с. индукции равна производной dФ/dt от магнитного потока
Еi = dФ/dt, (3.27)
то есть мы пришли к закону Фарадея. В проведенных рассуждениях мы для простоты оперировали модулями векторов Ес, v и В, поэтому ве-личину э.д.с. индукции в формуле (3.27) определили также лишь по модулю.
Рассмотренное объяснение механизма возникновения э.д.с. индукции относится к случаю, когда изменение магнитного потока происходит за счет подвижных проводников. Но магнитный поток может меняться также и путем изменения величины В при неизменной геометрии контура. Тогда сила Лоренца не возникает, а ин-дукционный ток возбуждается в этом случае вихревым электрическим полем, порождае-мым меняющимся во времени магнитным полем. Этот более общий случай возникновения э.д.с. индукции будет рассмотрен в следующем разделе (тема 4).
Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.
Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.
Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и др.
Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.
С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.
Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.
39. Вращение проводящей рамки в магнитном поле. Баллистический способ измерения магнитной индукции.
Явление электромагнитной индукции часто используется для преобразования механической энергии в энергию электрического тока. Для этой цели применяются генераторы, принцип действия которых рассмотрим на примере плоской рамки, которая вращается в однородном магнитном поле.
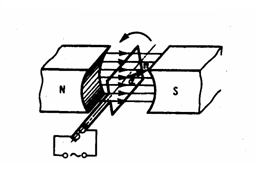
Рис.1
Пусть рамка вращается в однородном магнитном поле (B=const) равномерно с угловой скоростью ω=const. Магнитный поток, который сцеплен с рамкой площадью S, в любой произвольный момент времени t будет равен
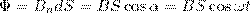
где α = ωt — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t=0 было α=0).
Во время вращения рамки в ней будет появляться переменная э.д.с. индукции
(1)
которая изменяется со временем по гармоническому закону. При sinαt = 1 э.д.с. ξi максимальна, т. е.
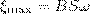(2)
Учитывая (2), формула (1) запишется как
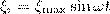
Значит, если рамка вращается равномерно в однородном магнитном поле, то в ней возникает переменная э.д.с., которая изменяется по гармоническому закону.
Из формулы (2) следует, что ξmax (следовательно, и э.д.с. индукции) находится в непосредственной зависимости от величин ω, B и S. В России принята стандартная частота тока ν = ω/(2π) = 50 Гц, поэтому на практике возможно лишь увеличение двух остальных величии. Для увеличения В применяют мощные постоянные магниты или пропускают значительный ток в электромагнитах, а также внутрь электромагнита помещают сердечники из материалов с большим значением магнитной проницаемостью μ. Если вращать не один, а большое количество витков, соединенных последовательно, то тем самым увеличивается S. Переменное напряжение снимается с вращающегося витка с помощью щеток, схематически изображенных на рис. 1.
Процесс превращения механической энергии в электрическую обратим. Если по рамке, которая помещена в магнитное поле, пропускать электрический ток, то в магнитном поле на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателей, имеющих предназначение превращать электрическую энергии в механическую.
Баллистический метод основан на измерении баллистическим гальванометром количества электричества, индуктируемого в измерительной катушке при быстром изменении сцепленного с ней магнитного потока (см. Баллистический метод электроизмерений). Кроме баллистических гальванометров, для измерения магнитного потока применяют веберметры (флюксметры) - магнитоэлектрические и фотоэлектрические. Веберметрами можно измерять медленно меняющиеся потоки. Баллистическим методом определяют основную кривую индукции В (Н), кривую намагничивания J (H), петлю гистерезиса, различные виды проницаемости и размагничивающий фактор ферромагнитных образцов.
40. Явление самоиндукции. ЭДС самоиндукции.
Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока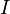 
:
.
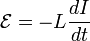Коэффициент пропорциональности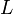 
называется коэффициентом самоиндукции или индуктивностью контура (катушки).
ЭДС индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
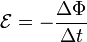
где 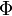— поток магнитного поля через замкнутую поверхность 
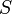, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле
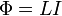
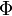— магнитный поток, 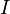— ток в контуре, 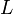— индуктивность.
§ Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
.
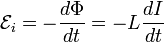Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
.
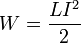Дата: 2019-07-24, просмотров: 201.
