Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
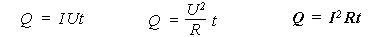 На первый взгляд все формулы могут считаться равноправными, однако только последняя справедлива всегда, поэтому она и считается законом. А вот остальные две справедливы только при определенных условиях, поэтому законом считаться не могут.
На первый взгляд все формулы могут считаться равноправными, однако только последняя справедлива всегда, поэтому она и считается законом. А вот остальные две справедливы только при определенных условиях, поэтому законом считаться не могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
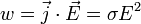 Где:
Где:
· 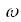 - является мощностью тепла, выделяемого в единице объёма;
- является мощностью тепла, выделяемого в единице объёма;
· 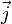 - плотность электрического тока;
- плотность электрического тока;
· 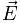 - это напряжённость электрического поля;
- это напряжённость электрического поля;
· 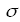 - проводимость выбранной среды.
- проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r.
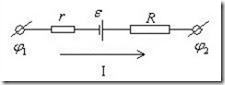
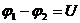 - напряжение на концах участка цепи.
- напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
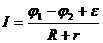
При соединении концов неоднородного участка цепи идеальнымпроводником образуется замкнутая цепь, в которой  потенциалы φ1 иφ2 выравниваются и мы приходим к закону Ома для замкнутой (или полной) цепи:
потенциалы φ1 иφ2 выравниваются и мы приходим к закону Ома для замкнутой (или полной) цепи:
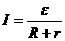
Если сопротивление внешней цепи 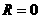 , то имеем случай короткого замыкания. В этом случае в цепи течетмаксимальный ток:
, то имеем случай короткого замыкания. В этом случае в цепи течетмаксимальный ток:
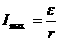
При 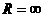 имеем разомкнутую цепь. В этом случае ток в цепи равен нулю:
имеем разомкнутую цепь. В этом случае ток в цепи равен нулю:
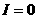
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
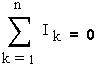
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
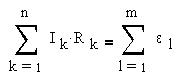
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
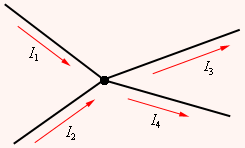
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
| Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
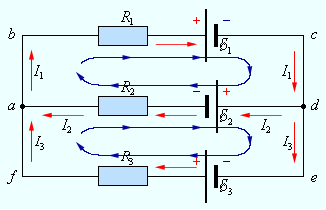
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
| Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
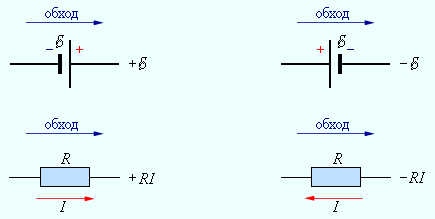
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
| Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc: I1R1 = Δφbc – 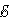 1.
1.
Для участка da: I2R2 = Δφda – 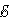 2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – 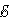 1 + 1 + 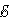 2 = – 2 = – 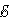 1 – 1 – 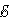 2. 2.
|
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = 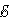 2 + 2 + 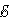 3. 3.
|
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – 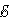 1 – 1 – 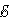 2, 2,
|
– I2R2 + I3R3 = 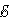 2 + 2 + 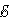 3, 3,
|
| – I1 + I2 + I3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I2 R = U2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля - Ленца.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
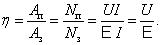
| (7.8.1) |
Полезная работа – мощность, выделяемая на внешнем сопротивлении Rв единицу времени. По закону Ома имеем: 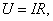 а
а 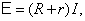 тогда
тогда
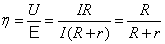 .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное
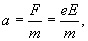
и к концу пробега скорость упорядоченного движения достигнет значения
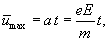
| (18.2) |
где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости 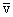 . В этом приближении
. В этом приближении 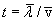 , где
, где 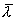 - среднее значение длины свободного пробега,
- среднее значение длины свободного пробега, 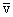 - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)
- скорость теплового движения электронов. Подставим это значение t в формулу (18.2)
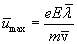
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
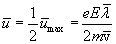
Подставив это выражение в
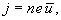
получим
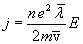
Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно 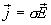 коэффициент пропорциональности между j и Е представляет собой проводимость
коэффициент пропорциональности между j и Е представляет собой проводимость
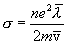
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
25. Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К концу свободного пробега электрон приобретает скорость 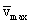 , и, следовательно, дополнительную кинетическую энергию, средняя величина которой
, и, следовательно, дополнительную кинетическую энергию, средняя величина которой
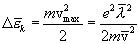
Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, и передает энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании. Каждый электрон претерпевает за секунду в среднем 1/t соударений, сообщая всякий раз решетке энергию 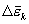 . Следовательно, в единице объема за единицу времени должно выделяться тепло
. Следовательно, в единице объема за единицу времени должно выделяться тепло
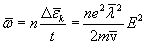
где n - число электронов проводимости в единице объема. Величина 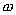 есть не что иное, как удельная мощность тока. Множитель при
есть не что иное, как удельная мощность тока. Множитель при 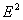 совпадает со значением
совпадает со значением 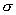 (18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.
(18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.
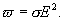
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
26. Несамостоятельный и самостоятельный газовые разряды.
Несамостоятельный газовый разряд.
Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа.
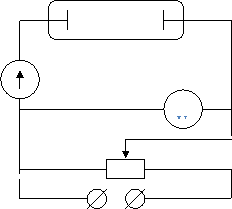
Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
+ -
Самостоятельный газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.

I

|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила 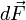 , с которой магнитное поле действует на элемент объёма
, с которой магнитное поле действует на элемент объёма 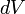 проводника с током плотности
проводника с током плотности 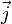 , находящегося в магнитном поле с индукцией
, находящегося в магнитном поле с индукцией 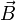 :
:
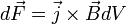 .
.
Модуль силы Ампера можно найти по формуле:
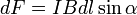 ,
,
где 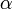 — угол между векторами магнитной индукции и тока.
— угол между векторами магнитной индукции и тока.
Сила 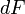 максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (
максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ( 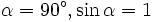 ):
):
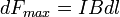 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная инду́кция 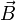 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 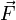 магнитное поле действует на заряд
магнитное поле действует на заряд 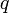 , движущийся со скоростью
, движущийся со скоростью 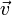 .
.
Более конкретно, 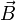 — это такой вектор, что сила Лоренца
— это такой вектор, что сила Лоренца 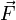 , действующая со стороны магнитного поля[1] на заряд
, действующая со стороны магнитного поля[1] на заряд 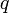 , движущийся со скоростью
, движущийся со скоростью 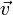 , равна
, равна
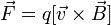
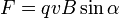
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора 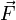 перпендикулярно им обоим и направлено по правилу буравчика).
перпендикулярно им обоим и направлено по правилу буравчика).
Принцип суперпозиции
Для магнитного поля, как и для электрического поля, справедлив принцип суперпозиции: поле 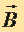 , порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей
, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей 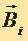 , порождаемых каждым зарядом (током) в отдельности:
, порождаемых каждым зарядом (током) в отдельности: 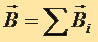
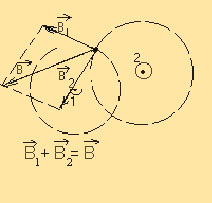
т.е., чтобы найти силу, действующую на точку в пространстве, нужно сложить силы, действующие на неё, как показано на рисунке
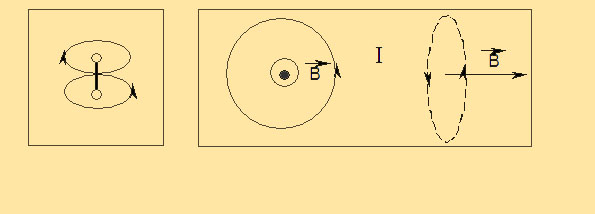
Магнитное поле кругового тока представляет собой некую восьмёрку с разделением колец в центре кольца, по которому течёт ток. Его схема показана на рисунке
28. Сила Лоренца. Движение заряженных частиц в магнитом поле.
Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженнуючастицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью 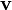 заряд
заряд 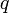 лишь со сторонымагнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороныэлектрического
лишь со сторонымагнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороныэлектрического 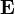 и магнитного
и магнитного 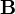 полей. Выражается в СИ как:
полей. Выражается в СИ как:
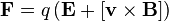
Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.
Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и Вравен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила ЛоренцаF=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv2/r , следовательно
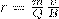 (1)
(1)
Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,
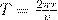
Подствавив (1), получим
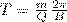 (2)
(2)
т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц.
В случае, если скорость v заряженной частицы направлена под углом α к вектору В (рис. 170), то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью vparall=vcosα ; 2) равномерного движения со скоростью vperpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить vperpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии
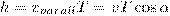
Подставив в данное выражение (2), найдем
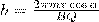
Направление, в котором закручивается спираль, определяется знаком заряда частицы.
Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.
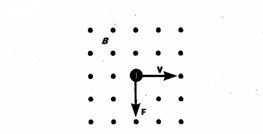
Рис.1
29. Эффект Холла и его применение.
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 годув тонких пластинках золота.
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле 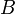 течёт электрический ток под действием напряжённости
течёт электрический ток под действием напряжённости 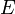 . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
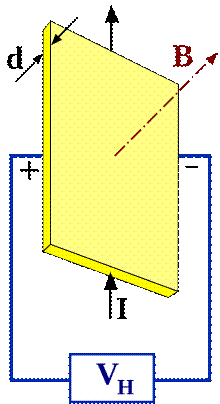

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов 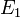 не скомпенсирует магнитную составляющую силы Лоренца:
не скомпенсирует магнитную составляющую силы Лоренца:
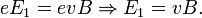
Скорость электронов 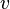 можно выразить через плотность тока:
можно выразить через плотность тока:
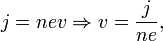
где 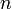 — концентрация носителей заряда. Тогда
— концентрация носителей заряда. Тогда
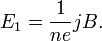
Коэффициент 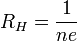 пропорциональности между
пропорциональности между 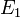 и
и 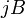 называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак
называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак 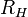 , что объясняется в полуклассической и квантовой теориях твёрдого тела.
, что объясняется в полуклассической и квантовой теориях твёрдого тела.
Аномальный эффект Холла
Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.
Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью[2].
[править]Квантовый эффект Холла
Основная статья: Квантовый эффект Холла
В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.
[править]Спиновый эффект Холла
Основная статья: Спиновый эффект Холла
В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.
Применение


Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.
Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле илиполупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников.
На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в коллекторном ДПТ.
Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей.
30. Закон Био-Савара-Лапласа
Магнитное поле постоянных токов различной формы исследовалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты их опытов были обобщены французским ученым П. Лапласом.
Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен
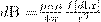 (1)
(1)
где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.
Модуль вектора dB задается выражением
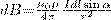 (2)
(2)
где α — угол между векторами dl и r.
Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
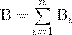 (3)
(3)
Используя данные формулы для расчет характеристик магнитного поля (В и Н) в общем случае достаточно сложен. Однако если распределение тока имеет какую-либо симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции дает возможность просто рассчитать некоторые поля. Рассмотрим два примера.
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому бесконечному проводу (рис. 2).
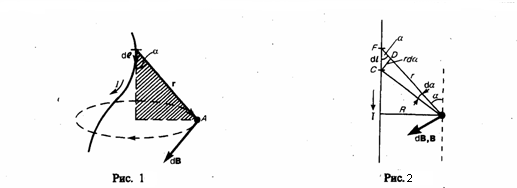
В произвольной точке А, удаленной на расстояние R от оси проводника, векторы dB от всех элементов тока имеют одинаковое направление, которое перпендикулярно плоскости чертежа («к вам»). Значит, сложение всех векторов dB можно заменить сложением их модулей. За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины. Из рис. 2 следует, что
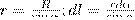
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти формулы в (2), получим, что магнитная индукция, которая создавается одним элементом проводника, равна
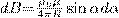 (4)
(4)
Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то, согласно (3) и (4),
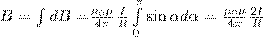
Значит, магнитная индукция поля прямого тока
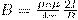 (5)
(5)
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как видно из рисунка, каждый элемент кругового проводника с током создает в центре магнитное поле одинакового направления - вдоль нормали от витка. Значит, сложение векторов dB также можно заменить сложением их модулей. Поскольку расстояние всех элементов проводника до центра кругового тока одинаково и равно R и все элементы проводника перпендикулярны радиусу-вектору (sinα=1), то, используя (2),
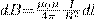
Тогда
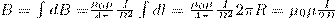
Следовательно, магнитная индукция поля в центре кругового проводника с током
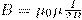
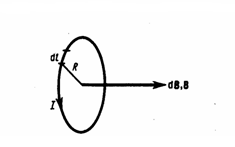
Рис.3
31. Закон Био-Савара-Лапласа и применение его к расчёту магнитного поля прямолинейного проводника стоком.
В произвольной точке А, удаленной на расстояние R от оси проводника, векторы dB от всех элементов тока имеют одинаковое направление, которое перпендикулярно плоскости чертежа («к вам»). Значит, сложение всех векторов dB можно заменить сложением их модулей. За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины. Из рис. 2 следует, что
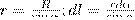
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти формулы в (2), получим, что магнитная индукция, которая создавается одним элементом проводника, равна
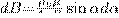 (4)
(4)
Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то, согласно (3) и (4),
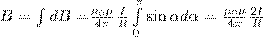
Значит, магнитная индукция поля прямого тока
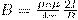 (5)
(5)
32. Закон Био-Савара-Лапласа и применение его к расчёту магнитного поля оси кругового витка с током
Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
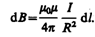
Тогда
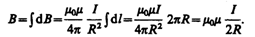
Следовательно, магнитная индукция поля в центре кругового проводника с током
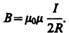

33. Магнитное поле движущегося заряда. Взаимодействие параллельных проводников с током.
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q , свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой
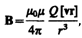 (113.1)
(113.1)
где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и r, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.
Модуль магнитной индукции (113.1) вычисляется по формуле
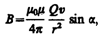 (113.2)
(113.2)
где a — угол между векторами v и r.
Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
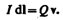
Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.

Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на — Q . Скорость v — относительная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.
Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф. Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.
Если близко один к другому расположены проводники с токами одного направления, то магнитные линии этих проводников, охватывающие оба проводника, обладая свойством продольного натяжения и стремясь сократиться, будут заставлять проводники притягиваться (рис. 90, а).
Магнитные линии двух проводников с токами разных направлений в пространстве между проводниками направлены в одну сторону. Магнитные линии, имеющие одинаковое направление, будут взаимно отталкиваться. Поэтому проводники с токами противоположного направления отталкиваются один от другого (рис. 90, б).
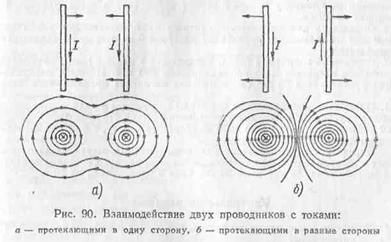
Рассмотрим взаимодействие двух параллельных проводников с токами, расположенными на расстоянии а один от другого. Пусть длина проводников равна l.
Магнитная индукция, созданная током I1 на линии расположения второго проводника, равна
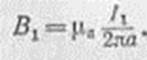
На второй проводник будет действовать электромагнитная сила
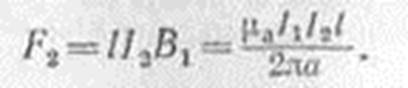
Магнитная индукция, созданная током I2 на линии расположения первого проводника, будет равна
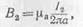
и на первый проводник действует электромагнитная сила
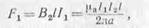
равная по величине силе F2
На электромеханическом взаимодействии проводников с токо^ основан принцип действия электродинамических измерительных прИб&ров; используемых в цепях постоянного и в особенности переменного тока.
34. Закон полного тока и применение его к расчёту магнитных полей длинного соленоида и тороида
Закон полного тока
Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.
Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.
Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.
На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.
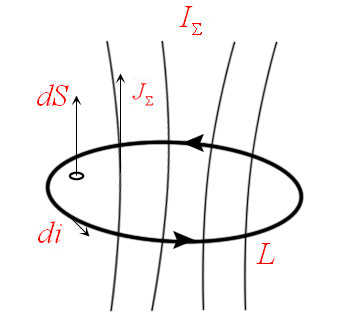
Далее представим то, что поверхность S пронизывается отдельной системой токов, которая может нести как дискретный характер (к примеру, систему отдельных проводников), так и быть непрерывно распределенной (электронный поток может послужить этому примером). Не обуславливая тем временем физической природы данных токов, будем подразумевать для конкретности, что они распределены непрерывно в пространстве с кое-какой плотностью 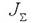
То теперь полный ток, пронизывающий контур, найдется в виде
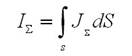
Закон полного тока говорит о том, что циркуляция по контуру L вектора напряженности магнитного поля, инициированного протеканием тока 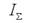 равна полному току, то есть.
равна полному току, то есть.
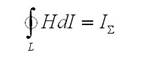
Закон полного тока формулирует соотношение выше в интегральной форме.
В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство
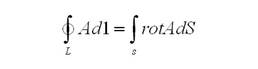
Использовав крайнюю формулу и перестроив с её помощью
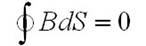
будем располагать
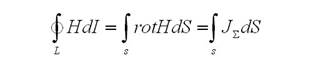
откуда получим из-за произвольности выбранного контура
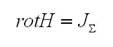
Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.
Ток смещения
Известен из практики факт прохождения электрического переменного тока по цепи, включающий в себя конденсатор. Значительно важным тут приходится то, что ток протекает между обкладками по пространству, в котором нет каких-либо носителей электрического заряда. Вследствие чего можно предположить, что в данной области течёт некий ток, натура которого принципиально непохожа на натуры тока проводимости, ранее освоенного. Данный ток впервые был влит в электродинамику Максвеллом, а назвал он его током смещения.
Мы видим цепь с конденсатором, представленную изображением ниже, в нём выделена замкнутая поверхность S, охватывающая одну из обкладок конденсатора.
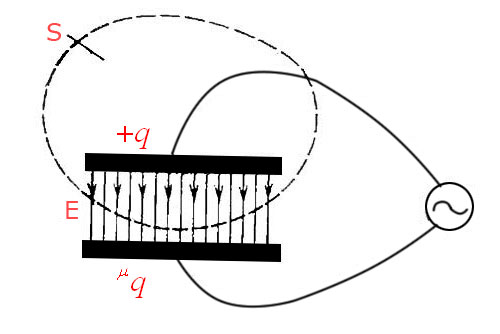
Из закона Гаусса надлежит, что если, когда между обкладками имеется вакуум,
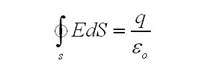
Ток в цепи в свою очередь, найдется следующим образом:
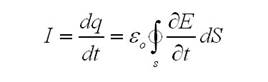
Последнее выражение показывает, что величина
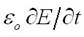
обладает размерностью плотности тока, который и должен называться током смещения.
Таким образом, плотность тока смещения в вакууме
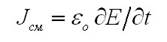
Предложением Максвелла было введение плотности тока смещения в правую часть закона полного тока наряду плотностью тока проводимости. Данное решение оказалось довольно значительным для электродинамики, поскольку при этом становилось возможным устанавить внутреннюю взаимосвязь магнитного и электрического поля. В действительности, к протеканию тока смещения, который, в свою очередь, вызывает появление магнитного поля, приводит изменение во времени электрического поля в какой-либо точке пространства.
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.
На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA , как показано на рис. 175. Циркуляция вектора В по замкнутому контуру ABCDA , охватывающему все N витков, согласно (118.1), равна
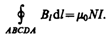
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA . На участках АВ и CD контур перпендикулярен линиям магнитной индукции и Bl =0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна В l (контур совпадает с линией магнитной индукции); следовательно,
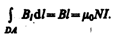 (119.1)
(119.1)
Из (119.1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):
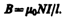 (119.2)
(119.2)
Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био - Савара - Лапласа; в результате получается та же формула (119.2).
Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.
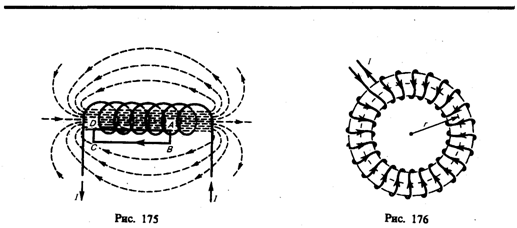
Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118.1), B ×2pr = m0NI , откуда следует, что магнитная индукция внутри тороида (в вакууме)
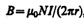
где N — число витков тороида.
Если контур проходит вне тороида, то токов он не охватывает и B ×2pr =0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).
35. Поток вектора магнитной индукции, его единица СИ. Теорема Гаусса для магнитного поля.
Магни́тный пото́к — поток 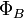 как интеграл вектора магнитной индукции
как интеграл вектора магнитной индукции 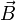 через конечную поверхность
через конечную поверхность 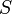 . Определяется через интеграл по поверхности
. Определяется через интеграл по поверхности
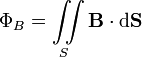
при этом векторный элемент площади поверхности определяется как
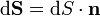
где 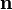 — единичный вектор, нормальный к поверхности.
— единичный вектор, нормальный к поверхности.
Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:
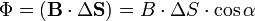
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.
Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:
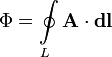
В СИ единицей магнитного потока является Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1),
в системе СГС — максвелл (Мкс); 1 Вб = 108 Мкс.
Дата: 2019-07-24, просмотров: 452.