Но оценка устойчивости по скоростям вращения входящих в нее СГ – чаще всего уже состоявшийся факт осуществления синхронизма или выход из него. Поэтому важно иметь такие критерии, по которым можно оценить устойчивость энергосистемы.

Рассмотрим схему простейшей одномашинной системы. Под простейшей системой понимается такая, в которой синхронная машина Г связана с системой С через трансформаторы Т1 и Т2 и линии электропередач Л (рис. 2.7).

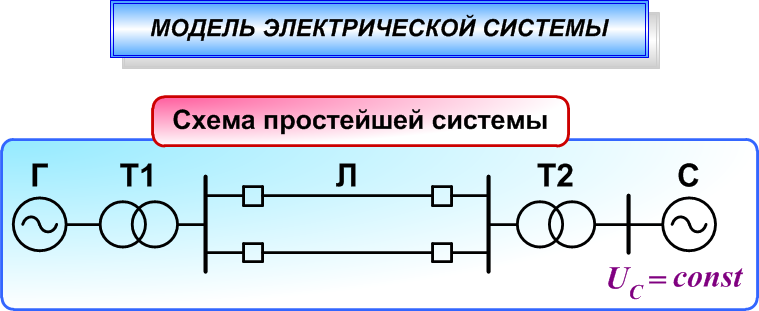
Рис. 2.7. Схема простейшей электроэнергетической системы

Принимается, что:

– автоматическое регулирование возбуждения генератора (АРВ) отключено, следовательно, i_f = const и E_q = const;

– суммарная мощность генераторов системы во много раз превышает мощность синхронной машины Г P_С = (5–10)P_Г; это позволяет считать напряжение на шинах сис­темы неизменным (U = const);

– все элементы линейные z_i(I) = const, в частности, отсутствует насыщение в магнитных цепях, что позволяет использовать метод наложения;

– пренебрегаем активными потерями в элементах и зарядной мощностью линий: r = 0 и Q_C = 0;

– исходный режим синхронный ω_f = ω _с.

Рассмотрим схему замещения такой системы. На рис. 2.8 можно увидеть, что каждый элемент системы имеет свои параметры.

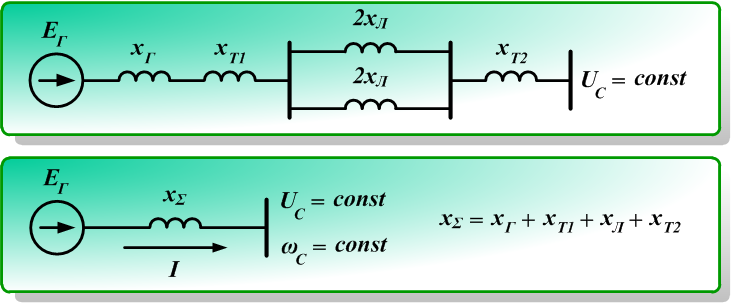
Рис. 2.8. Схема замещения простейшей электроэнергетической системы с расчетом суммарного эквивалентного сопротивления: E_Г – ЭДС генератора; х_Г – сопротивление генератора; х_Т1 – сопротивление повышающего трансформатора; х_Л – сопротивление линии электропередачи (ЛЭП); х_Т2 – сопротивление понижающего трансформатора; U_c – напряжение на шинах приемной энергосистемы является неизменным; х_Σ – суммарное эквивалентное сопротивление

Из схемы замещения передачи (рис. 2.8) результирующим сопротивлением передачи является х_Σ.

Для получения характеристики мощности представим векторную диаграмму электропередачи (рис. 2.9). При её построении полный вектор тока I разложен на действительную I_a и мнимую I_p составляющие.

Рис. 2.9. Векторная диаграмма передачи электрической энергии: φ – угол между напряжением U и током I; I – суммарный ток нагрузки; I_а – активная часть тока нагрузки; I_р – реактивная часть тока нагрузки; δ – угол нагрузки (между напряжением приемной системы и ЭДС генератора)

Из рис. 2.9 следует, что

I_a х _Σ = E_Г sin d,                                       (2.1)

где d – угол между ЭДС синхронной машины Е и напряжением системы U.

Умножая обе части этого равенства на U/х_Σ, получим

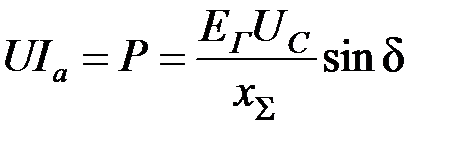,                                    (2.2)                      

где Р – активная мощность, выдаваемая генератором.

Зависимость (2.2) имеет синусоидальный характер и называет­ся характеристикой мощности, или моментно-угловой характеристикой синхронной машины (мощность и момент синхронной машины пропорциональны, а в относительных единицах равны). При неизмен­ных ЭДС синхронной машины E_Г, напряжении системы U_С и сопротивлении х_Σ угол d определяется для генератора только выдаваемой активной мощностью.

Мощность, выдаваемая генератором, имеет максимум

,                                          (2.3)

который называется пределом мощности (идеальный предел мощности) простейшей электрической системы (рис. 2.10).

Наглядной иллюстра­цией зависимости мощности (момента) турбины от угла сдвига δ является система двух дисков (рассмотрено в разд. 2.1), соединенных пружинами (рис. 2.2). В режиме холостого хода (без учета трения) ведущий диск (поле ротора, свя­занного с турбиной) и ведомый диск (поле статора) не обра­зуют угла сдвига относительно друг друга.
При появлении тормозящего момента (нагрузки генератора) угол сдвига между диска­ми будет тем больше, чем больше тормозящий момент.
Очевидно, что при увеличении тормозящего момента может произойти про­ворот одного диска относительно другого, что является нарушени­ем устойчивости рассматриваемой системы.

Рис. 2.10. Характеристика мощности синхронной машины (синхронного генератора): P – активная мощность, выдаваемая генератором; P_т – механическая мощность турбины генератора; P_m – идеальный предел мощности; P₀ – первоначальное значение вырабатываемой мощности генератора; δ – угол нагрузки (между напряжением приемной системы и ЭДС генератора); δ₀ – угол нагрузки, находящийся в точке пересечения графиков Р и Р_т, данный угол находится на восходящей части функции Р(δ)

Таким образом, зависимость P( δ ) характеризует возможность генератора выдавать активную мощность в систему, сохраняя устойчивость.

Контрольные вопросы

1. Какие процессы называют электромеханическими переходными? Назовите причины, их вызывающие.

2. Что такое возмущающие воздействия, малые и большие возмущения? Приведите примеры.

3. Для чего важно соблюдать балансы активных и реактивных мощностей?

4. Перечислите основные режимы электроэнергетических систем.

5. Что такое статическая устойчивость? Для чего она рассчитывается?

6. Изобразите векторную диаграмму простейшей электропередачи.

7. Поясните термин «пропускная способность элемента системы».

СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ

ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ

и узлов нагрузки