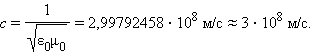1.1
Механическое движение
Механическое движение-это процесс изменения положения тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условное принятое за неподвижное- тело отсчета.
Тело отсчета -это тело, относительно которого определяется положение другого тела.
Система отсчета -это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Траектория движения
Траектория движения тела -это непрерывная линия, которую описывает движущееся тело(рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Пройденный путь
Пройденный путь -скалярная величина, равная длине дуги траектории, пройденной телом за некоторое время.
Перемещение
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением, векторная величина.
Средняя и мгновенная скорости движения.Направление и модуль скорости.
Скорость- физическая величина, которая характеризует быстроту изменения координаты.
Средняя скорость движения - это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за которое это перемещение произошло. Направление вектора средней скорости совпадает с направлением вектора перемещения ∆ S
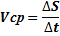
Мгновенная скорость -это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени ∆ t . Вектор мгновенной скорости направлен по касательной к траектории. Модуль равен первой производной пути по времени.
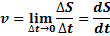
Формула пути при равноускоренном движении.
Равноускоренное движение -это движение, при котором ускорение постоянно по модулю и направлению.
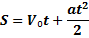
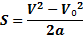
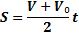
1.2.
Ускорение движения
Ускорение движения- векторная физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.
Формула скорости при равноускоренном движении
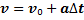
1.4
Первый закон Ньютона (или закон инерции)
Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.
Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью).
В природе существуют четыре вида взаимодействия
1. Гравитационное (сила тяготения) – это взаимодействие между телами, которые обладают массой.
2. Электромагнитное- справедливо для тел, обладающих электрическим зарядом, ответственно за такие механические силы, как сила трения и сила упругости.
3.Сильное- взаимодействие короткодействующее, то есть действует на расстоянии порядка размера ядра.
4. Слабое. Такое взаимодействие ответственно за некоторые виды взаимодействия среди элементарных частиц, за некоторые виды β-распада и за другие процессы, происходящие внутри атома, атомного ядра.
Масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие.
Сила – является количественной мерой действия одного тела на другое.
Второй закон Ньютона.
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: F = ma
Измеряется в 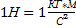
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).
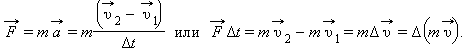 Выражение второго закона Ньютона через изменение импульса тела
Выражение второго закона Ньютона через изменение импульса тела
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равноускоренное движение — движение, при котором ускорение постоянно по модулю и направлению.
1.5
Третий закон Ньютона. Примеры.
Плечо силы.
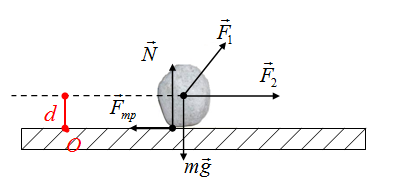
Плечо силы - это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
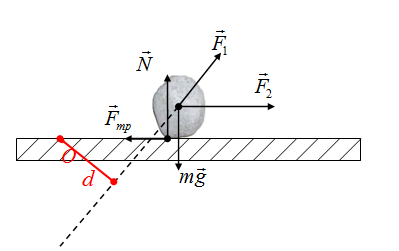
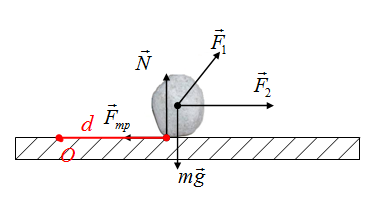
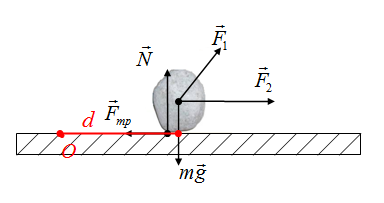 Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести - это длина перпендикуляра (отрезок d) на рисунке
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести - это длина перпендикуляра (отрезок d) на рисунке

Момент инерции тел.
Момент инерции J (кгм2) – параметр, аналогичный по физическому смыслу массе при поступательном движении. Он характеризует меру инерции тел, вращающихся относительно фиксированной оси вращения. Момент инерции материальной точки с массой m равен произведению массы на квадрат расстояния от точки до оси вращения: 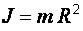 .
.
Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. Он может быть выражен через массу тела и его размеры
Теорема Штейнера.
Момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
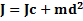
Jc— известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m— масса тела,
d— расстояние между указанными осями.
Закон сохранения момента импульса. Примеры.
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
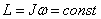 .
.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).

|
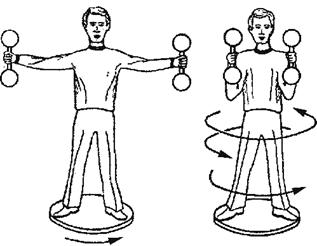 Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).
Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).
1.9.
Работа силы.
Работа силы - мера действия силы при превращении механического движения в другую форму движения.
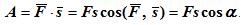
Примеры формул работы сил.
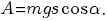
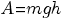 работа силы тяжести; работа силы тяжести наклонной пов-ти
работа силы тяжести; работа силы тяжести наклонной пов-ти
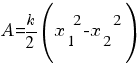
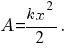 работа силы упругости
работа силы упругости
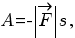 работа силы трения
работа силы трения
1.10.
1.11.
Механическая энергия тела.
Механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.
1.12.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
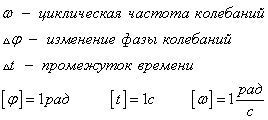 Циклическая частота характеризует скорость изменения фазы колебаний.
Циклическая частота характеризует скорость изменения фазы колебаний.
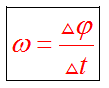
Начальное состояние колебательной системы характеризует начальная фаза 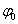
Амплитуда колебаний A - это наибольшее смещение из положения равновесия
Период T - это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний - это число полных колебаний в единицу времени t.
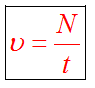

Частота, циклическая частота и период колебаний соотносятся как
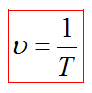
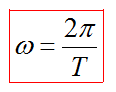
1.13.
1.14.
Физический маятник.
Физический маятник - твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс.
1.15.
2.1.
Электрический заряд.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q.
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
· Существует два рода электрических зарядов, условно названных положительными и отрицательными.
· Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
· Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Закон Кулона.
Модуль силы взаимодействия двух точечных неподвижных электрических зарядов в вакууме прямо пропорционален произведению величин этих зарядов и обратно пропорционален квадрату расстояния между ними.
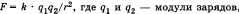
г — расстояние между ними, k — коэффициент пропорциональности, зависящий от выбора системы единиц, в СИ 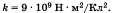
Величина, показывающая, во сколько раз сила взаимодействия зарядов в вакууме больше, чем в среде, называется диэлектрической проницаемостью среды Е. Для среды с диэлектрической проницаемостью е закон Кулона записывается следующим образом:
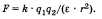
В СИ коэффициент k принято записывать следующим образом: 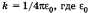
— электрическая постоянная, численно равная 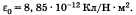
использованием электрической постоянной закон Кулона имеет вид:
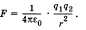
2.2.
Электростатическое поле.
Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.
Основные характеристики электростатического поля:
· напряженность
· потенциал
Примеры формул напряженности поля заряженных тел.
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
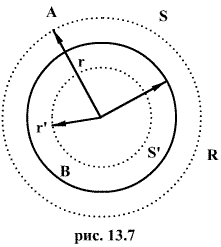 Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 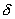 заряда в любой точке сферы будет одинакова.
заряда в любой точке сферы будет одинакова.
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
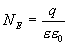
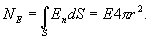
По теореме Гаусса
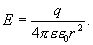
Следовательно
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
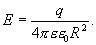 Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. 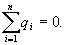 Следовательно, по теореме Гаусса,
Следовательно, по теореме Гаусса, 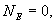 и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю.
и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю.
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью . 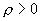
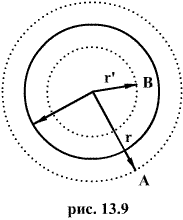
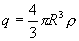 В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда ,расположенного в центре шара.
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда ,расположенного в центре шара.
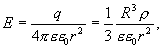
Тогда вне шара
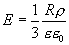
а на его поверхности (r=R)
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 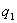 , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
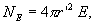
с другой стороны, в соответствии с теоремой Гаусса
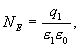
Из сопоставления последних выражений следует
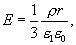
|
где 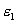 - диэлектрическая проницаемость внутри шара.
- диэлектрическая проницаемость внутри шара.
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью 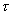 .
.
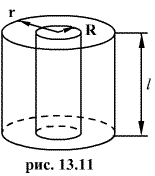
Проведем коаксиальную цилиндрическую поверхность радиуса 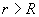 Поток вектора напряженности через эту поверхность
Поток вектора напряженности через эту поверхность
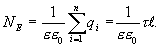
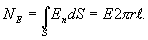
По теореме Гаусса
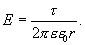 Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
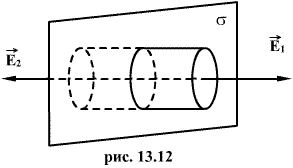
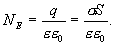 Суммарный поток вектора; напряженности равен вектору
Суммарный поток вектора; напряженности равен вектору 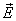 , умноженному на площадь S первого основания, плюс поток вектора
, умноженному на площадь S первого основания, плюс поток вектора 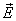 через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают.
через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают.
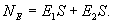 Таким образом, с другой стороны по теореме Гаусса
Таким образом, с другой стороны по теореме Гаусса
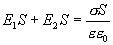
Следовательно
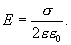 но
но 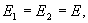 тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
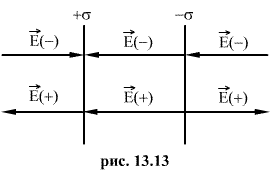 Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов
Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов 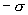 и
и 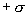 , равны сумме напряженностей полей, создаваемых пластинами, т.е.
, равны сумме напряженностей полей, создаваемых пластинами, т.е.
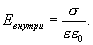
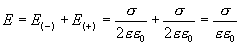
Таким образом,
Вне пластины векторы 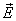 от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
2.3.
2.5.
Электрический ток.
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц
Сила тока.
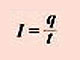 Сила тока ( I )- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
Сила тока ( I )- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
Плотность тока.
Плотность тока j — вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.
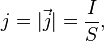
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).
2.7.
Закон Ома.
Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению . 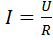
Закон Джоуля-Ленца.
При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. 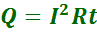
2.8.
Магнитное взаимодействие.
Магнитное взаимодействие — это взаимодействие упорядочение движущихся электрических зарядов.
Магнитное поле.
Магнитное поле - это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
Сила Лоренца и сила Ампера.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью 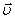 положительный заряд (здесь
положительный заряд (здесь 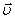 – скорость упорядоченного движения носителей положительного заряда). Модуль лоренцевой силы:
– скорость упорядоченного движения носителей положительного заряда). Модуль лоренцевой силы: 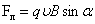
Сила Ампера- это сила, с которой магнитное поле действует на проводник с током.
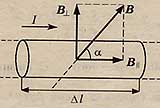

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индукции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки.
Закон Био-Савара-Лапласа.
Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
Формулировка
Пусть постоянный ток 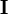 течёт по контуру γ, находящемуся в вакууме,
течёт по контуру γ, находящемуся в вакууме, 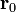 —точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
—точка, в которой ищется поле, тогда индукция магнитного поля в этой точкевыражается интегралом (в системе СИ)
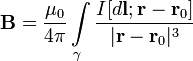
Направление 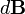 перпендикулярно
перпендикулярно 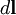 и
и 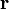 , то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление
, то есть перпендикулярноплоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилунахождения линий магнитной индукции (правилу правого винта):направление вращения головки винта дает направление 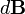 , еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора
, еслипоступательное движение буравчика соответствует направлению тока вэлементе. Модуль вектора 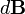 определяется выражением (в системе СИ)
определяется выражением (в системе СИ)
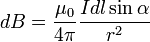
Векторный потенциал даётся интегралом (в системе СИ)
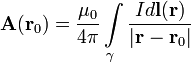
2.9.
Индуктивность контура.
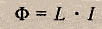 Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
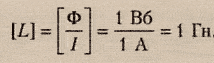 где Ф - магнитный поток через контур, I - сила тока в контуре.
где Ф - магнитный поток через контур, I - сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Энергия магнитного поля.
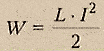 Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
2.10.
Электромагнитная индукция.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Правило Ленца.
Правило Ленца
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван. 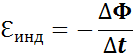
2.11.
2.12.
Первое уравнение Максвелла
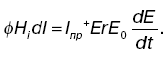 2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).
2. Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).
Второе уравнение Максвелла :
Электромагнитное излучение.
Электромагни́тные во́лны, электромагни́тное излуче́ние — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля.
3.1. Волна - это колебания, распространяющиеся в пространстве в течение времени.
Механические волны могут распространяться только в какой-нибудь среде (веществе): в газе, в жидкости, в твердом теле. Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды. Необходимым условием для появления упругих волн является возникновение в момент возмущения среды препятствующих ему сил, в частности, упругости. Они стремятся сблизить соседние частицы, когда они расходятся, и оттолкнуть их друг от друга в момент сближения. Силы упругости, действуя на удаленные от источника возмущения частицы, начинают выводить их из равновесия. Продольные волны характерны только газообразным и жидким средам, а вот поперечные – также и твердым телам: причина этого заключается в том, что частицы, составляющие данные среды, могут свободно перемещаться, так как жестко не зафиксированы, в отличие от твердых тел. Соответственно, поперечные колебания принципиально невозможны.
Продольные волны возникают тогда, когда частицы среды колеблются, ориентируясь вдоль вектора распространения возмущения. Поперечные волны распространяются в перпендикулярном вектору воздействия направлении. Короче: если в среде деформация, вызванная возмущением, проявляется в виде сдвига, растяжения и сжатия, то речь идет о твердом теле, для которого возможны как продольные, так и поперечные волны. Если же появление сдвига невозможно, то среда может быть любой.
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
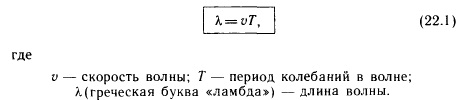
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду 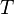 колебаний, поэтому
колебаний, поэтому
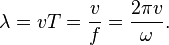
Волновое число (также называемое пространственной частотой) — это отношение 2π радиан к длине волны: 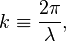 пространственный аналог круговой частоты.
пространственный аналог круговой частоты.
Определение: волновым числом k называется быстрота роста фазы волны φ по пространственной координате.
3.2. Плоская волна — волна, фронт которой имеет форму плоскости.
Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как фронт плоской волны начинается в 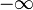 и заканчивается в
и заканчивается в 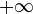 , чего, очевидно, быть не может.
, чего, очевидно, быть не может.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции 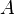 записывается в виде:
записывается в виде:
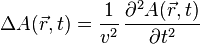 где
где
· 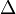 - оператор Лапласа;
- оператор Лапласа;
· 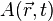 — искомая функция;
— искомая функция;
·  — радиус вектора искомой точки;
— радиус вектора искомой точки;
· 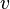 — скорость волны;
— скорость волны;
· 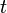 — время.
— время.
Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Частный случай волновой поверхности — волновой фронт.
А) Плоская волна – это волна, волновые поверхности которой представляют собой совокупность параллельных друг другу плоскостей. 
Б) Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических сфер.
Луч — линия, нормальной и волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская — параллельные прямые).
Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях, смысл понятия луч теряется.
3.3. Энергетические характеристики волны
Среда, в которой распространяется волна, обладает механической энергией, складывающейся из энергий колебательного движения всех ее частиц. Энергия одной частицы с массой m0 находится по формуле: Е0 = m0 Α2ω2/2. В единице объема среды содержится n = p/m0 частиц (ρ - плотность среды). Поэтому единица объема среды обладает энергией wр = nЕ0 = ρΑ2ω2/2.
Объемная плотность энергии (Wр) - энергия колебательного движения частиц среды, содержащихся в единице ее объема: 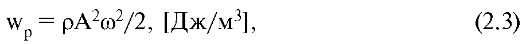
Поток энергии (Ф) - величина, равная энергии, переносимой волной через данную поверхность за единицу времени: 
Интенсивность волны или плотность потока энергии (I) - величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны: 
3.4. Электромагнитная волна
Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.
Условие возникновения электромагнитных волн. Изменения магнитного поля происходят при изменении силы тока в проводнике, а сила тока в проводнике изменяется при изменении скорости движения электрических зарядов в нем, т. е. при движении зарядов с ускорением. Следовательно, электромагнитные волны должны возникать при ускоренном движении электрических зарядов. При скорости заряда, равной нулю, существует только электрическое поле. При постоянной скорости заряда возникает электромагнитное поле. При ускоренном движении заряда происходит излучение электромагнитной волны, которая распространяется в пространстве с конечной скоростью.
Электромагнитные волны распространяются в веществе с конечной скоростью. 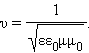 Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
| |
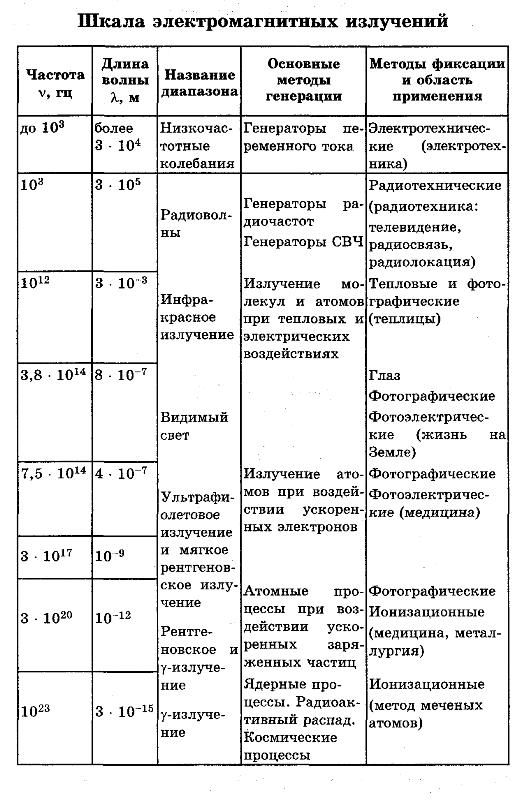
| Шкала электромагнитных волн: |
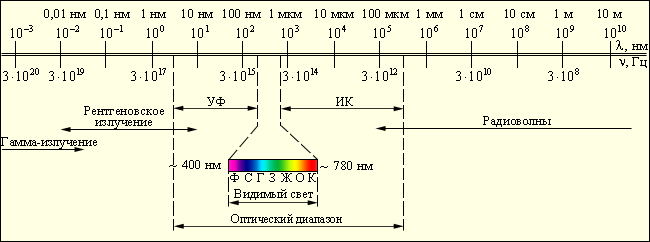
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше.
Электромагнитное излучение принято делить по частотам диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
3.6
Интерференция волн. Когерентные волны. Условия когерентности волн.
Оптическая длина пути (о.д.п.) света. Связь разности о.д.п. волн с разностью фаз колебаний, вызываемых волнами.
Амплитуда результирующего колебания при интерференции двух волн. Условия максимумов и минимумов амплитуды при интерференции двух волн.
Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей: а) красным светом, б) белым светом.
1) ИНТЕРФЕРЕНЦИЯ ВОЛН - такое наложение волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.
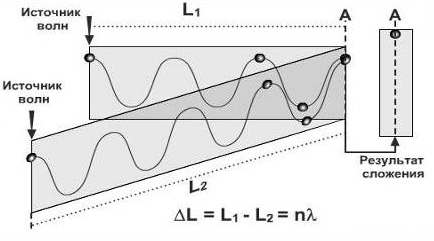
Необходимые условия для наблюдения интерференции:
1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);
2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).
Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью.
Дальше пример.
Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе).
Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление.
Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление.
Математически это выглядит так. Складываем две волны:
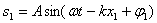
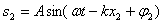
здесь х1 и х2 - расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:
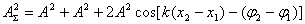
Максимум этого выражения есть 4 A 2, минимум - 0; всё зависит от разности начальных фаз и от так называемой разности хода волн :
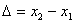
При 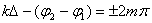 в данной точке пространства будет наблюдаться интерференционный максимум, при
в данной точке пространства будет наблюдаться интерференционный максимум, при 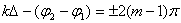 - интерференционный минимум.
- интерференционный минимум.
В нашем простом примере источники волн и точка пространства, где мы наблюдаем интерференцию, находятся на одной прямой; вдоль этой прямой интерференционная картина для всех точек одинакова. Если же мы сдвинем точку наблюдения в сторону от прямой, соединяющей источники, мы попадем в область пространства, где интерференционная картина меняется от точки к точке. В этом случае мы будем наблюдать интерференцию волн с равными частотами и близкими волновыми векторами.
2)1. Оптической длиной пути называется произведение геометрической длины d пути световой волны в данной среде на абсолютный показатель преломления этой среды n.
s=nd.
2. Разность фаз 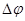 двух когерентных волн от одного источника, одна из которых проходит длину пути
двух когерентных волн от одного источника, одна из которых проходит длину пути 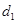 в среде с абсолютным показателем преломления
в среде с абсолютным показателем преломления 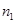 , а другая – длину пути
, а другая – длину пути 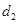 в среде с абсолютным показателем преломления
в среде с абсолютным показателем преломления 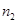 :
:
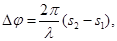
где 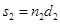 ,
, 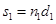 , λ – длина волны света в вакууме.
, λ – длина волны света в вакууме.
3)Амплитуда результирующего колебания зависит от величины, называемой разностью хода волн.
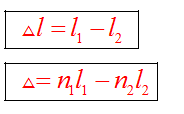

Если разность хода равна целому числу волн, то волны приходят в точку синфазно. Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой.
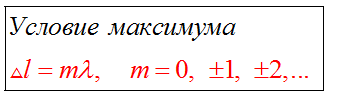
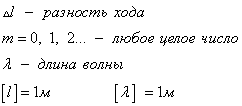
Если разность хода равна нечетному числу полуволн, то волны приходят в точку А в противофазе. В этом случае они гасят друг друга, амплитуда результирующего колебания равна нулю.
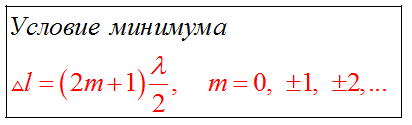
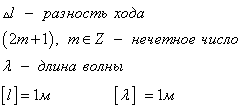
В других точках пространства наблюдается частичное усиление или ослабление результирующей волны.
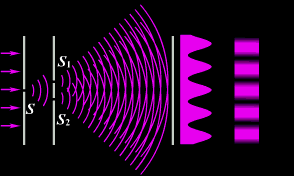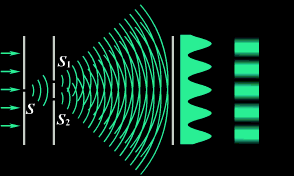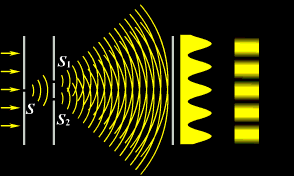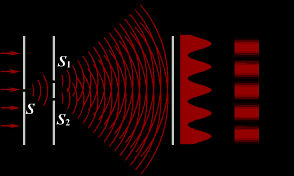
4)Опыт Юнга
В 1802 г. английский ученый Томас Юнг поставил опыт, в котором наблюдал интерференцию света. Свет из узкой щели S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок расширялся, и на белом экране световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
3.7
Осуществление интерференции света от обычных источников света.
Интерференция света на тонкой пленке. Условия максимумов и минимумов интерференции света на пленке в отраженном и в проходящем свете.
Интерференционные полосы равной толщины и интерференционные полосы равного наклона.
1)Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
2) 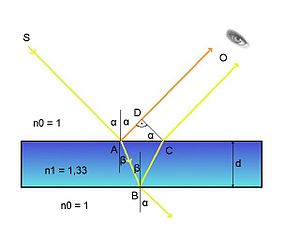 интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной
интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённыхобъективов. Луч света, проходя через плёнку толщиной 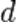 , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при
, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 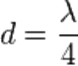 , где
, где 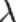 — длина волны. Если
— длина волны. Если 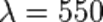 нм, то толщина плёнки равняется 550:4=137,5 нм.
нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от 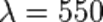 нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
 — условие максимума;
— условие максимума;
 — условие минимума,
— условие минимума,
где k=0,1,2… и 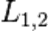 — оптическая длина пути первого и второго луча, соответственно.
— оптическая длина пути первого и второго луча, соответственно.
3)Полосы равного наклона
Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 8.8).
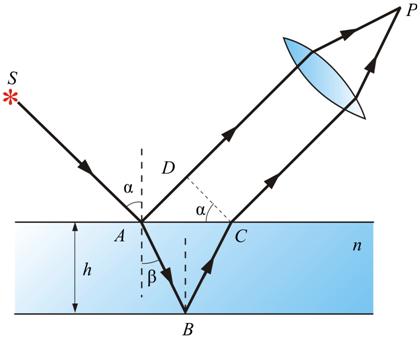
Рис. 8.8
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точкеP такая же, как на линии DC:
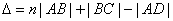 .
.
Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. 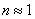 . Так как
. Так как 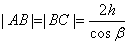 ,
, 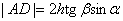 (h – толщина пластинки,
(h – толщина пластинки, 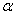 и
и 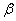 – углы падения и преломления на верхней грани;
– углы падения и преломления на верхней грани; 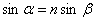 ), то для разности хода получаем
), то для разности хода получаем
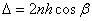 .
.
Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
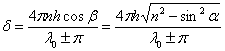 ,
,
где 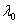 – длина волны в вакууме.
– длина волны в вакууме.
В соответствии с последней формулой светлые полосы расположены в местах, для которых 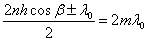 , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
, где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис. 8.9). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало 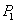 посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя
посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя 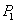 , дает
, дает 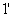 , а луч 2, отражаясь от з2 и далее от
, а луч 2, отражаясь от з2 и далее от 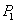 , дает
, дает 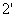 . Пластинки
. Пластинки 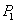 и
и 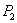 одинаковы по размерам.
одинаковы по размерам. 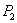 ставится для компенсации разности хода второго луча. Лучи
ставится для компенсации разности хода второго луча. Лучи 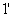 и
и 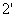 когерентны и интерферируют.
когерентны и интерферируют.
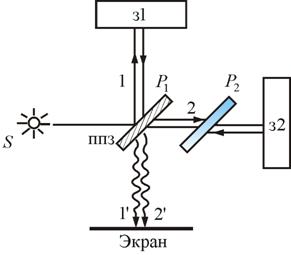
Рис. 8.9
Теория Планка
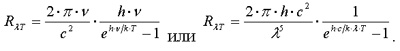 Немецкий ученый в 1900 году выдвинул гипотезу о том, что тела излучают не непрерывно, а отдельными порциями - квантами. Энергия кванта пропорциональна частоте излучения: E = hν = h·c/λ , где h = 6,63*10-34 Дж·с постоянная Планка. Руководствуясь представлениями о квантовом излучении R λT, он получил уравнение для спектральной плотности энергетической светимости R λT: Немецкий ученый в 1900 году выдвинул гипотезу о том, что тела излучают не непрерывно, а отдельными порциями - квантами. Энергия кванта пропорциональна частоте излучения: E = hν = h·c/λ , где h = 6,63*10-34 Дж·с постоянная Планка. Руководствуясь представлениями о квантовом излучении R λT, он получил уравнение для спектральной плотности энергетической светимости R λT:
|
Эта формула находится в соответствии с опытными данными во всем интервале длин волн при всех температурах.
Солнце - основной источник теплового излучения в природе. Солнечное излучение занимает широкий диапазон длин волн: от 0,1нм до 10м и более. 99% солнечной энергии приходится на диапазон от 280 до 6000нм. На единицу площади Земной поверхности приходится в горах от 800 до 1000 Вт/м2. До земной поверхности доходит одна двухмиллиардная часть тепла - 9,23 Дж/см2. На диапазон теплового излучения от 6000 до 500000нм приходится 0,4% энергии Солнца. В атмосфере Земли большая часть ИК-излучения поглощается молекулами воды, кислорода, азота, диоксида углерода. Радиодиапазон тоже большей частью поглощается атмосферой.
Количество энергии, которую приносят солнечные лучи за 1с на площадь в 1 кв.м, расположенную за пределами земной атмосферы на высоте 82 км перпендикулярную солнечным лучам называется солнечной постоянной. Она равна 1,4*103 Вт/м2.
Спектральное распределение нормальной плотности потока солнечного излучения совпадает с таким для R λT при температуре 6000 градусов. Поэтому Солнце относительно теплового излучения - R λT.
4.2. Фотоэлектрический эффект. Вольтамперная характеристика фототока. Опытные закономерности фотоэффекта .
Уравнение Эйнштейна для фотоэффекта.
Фотоэлектрический эффект (фотоэффект) — Явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества. Для твердых и жидких тел различают внешний и внутренний фотоэффект. Внешний фотоэффект заключается в испускании электронов с поверхности вещества. При внутреннем фотоэффекте электроны, оставаясь в веществе, изменяют свое энергетическое состояние. В газах фотоэффект состоит в фотоионизации — ионизации атомов или молекул под действием света.
внешний фотоэффект подчиняется следующим законам:
1) максимальная начальная скорость освобожденных электронов (фотоэлектронов) не зависит от интенсивности света, а зависит только от его частоты;
2) число фотоэлектронов, вырываемых из катода за 1с, пропорционально интенсивности света;
3) для каждого вещества существует минимальная Частота падающего света («красная» граница фотоэффекта), начиная с которой возможен фотоэффект. Эти законы не могут быть объяснены с точки зрения волновой природы света.
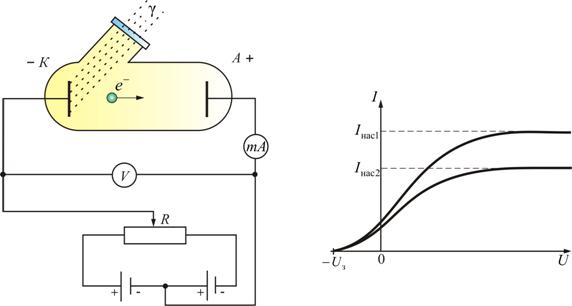 Вольт-амперная характеристика (ВАХ) фотоэффекта – зависимость фототока I, образуемого потоком электронов, от напряжения, – приведена на рис. 2.2.
Вольт-амперная характеристика (ВАХ) фотоэффекта – зависимость фототока I, образуемого потоком электронов, от напряжения, – приведена на рис. 2.2.
Такая зависимость соответствует двум различным энергетическим освещенностям катода (частота света в обоих случаях одинакова). По мере увеличения U фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями.
Максимальное значение фототока насыщения 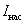 определяется таким значением напряжения U, при котором все электроны, испускаемые катодом, достигают анода:
определяется таким значением напряжения U, при котором все электроны, испускаемые катодом, достигают анода:
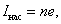
|
где n – число электронов, испускаемых катодом в 1 с. Из ВАХ следует, при U = 0 фототок не исчезает. Следовательно, электроны, выбитые из катода, обладают некоторой начальной скоростью υ, а значит и отличной от нуля кинетической энергией, поэтому они могут достигнуть катода без внешнего поля. Для того, чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение 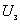 . При
. При 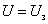 ни один из электронов, даже обладающий при вылете из катода максимальной скоростью , не может преодолеть задерживающего поля и достигнуть анода. Следовательно,
ни один из электронов, даже обладающий при вылете из катода максимальной скоростью , не может преодолеть задерживающего поля и достигнуть анода. Следовательно,
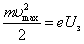 , ,
| (2.1.1) |
т.е. замерив задерживающее напряжение 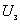 , можно определить максимальные значения скорости и кинетической энергии фотоэлектрона.
, можно определить максимальные значения скорости и кинетической энергии фотоэлектрона.
При изучении ВАХ разнообразных материалов при разных частотах падающего на катод излучения и разных энергетических освещенностях катода и обобщении полученных данных были установлены три закона внешнего фотоэффекта.
Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.
Согласно предположению Эйнштейна свет состоит из неделимых квантов энергии величиной hv. Это предположение позволило ему очень просто разрешить проблему фотоэффекта. Применим к фотоэффекту закон сохранения энергии, считая свет потоком фотонов с энергией

 В металле электрон находится в потенциальной яме. Для того, чтобы удалить электрон из металла, надо совершить работу против сил электростатического притяжения отрицательного электрона к положительному ионному остатку. Эта работа А называется работой выхода электрона из металла. Будем пока считать, что глубина потенциальной ямы равна этой работе А, впоследствии (см. рис. 12.1 и формулу (12.4)) мы внесем некоторые уточнения. Для разных металлов величина А разная. Меньше всего величина работы выхода у щелочных металлов, например, для цезия (Cs) А = 1,81 эВ. У цинка, который использовался в опытах Столетова, А = 4,24 эВ. Фотоны поглощаются поодиночке (если интенсивность света не достигает очень больших значений). Энергия фотона hv частично расходуется на работу выхода, оставшаяся часть (mv2max)/2 уносится электроном,
В металле электрон находится в потенциальной яме. Для того, чтобы удалить электрон из металла, надо совершить работу против сил электростатического притяжения отрицательного электрона к положительному ионному остатку. Эта работа А называется работой выхода электрона из металла. Будем пока считать, что глубина потенциальной ямы равна этой работе А, впоследствии (см. рис. 12.1 и формулу (12.4)) мы внесем некоторые уточнения. Для разных металлов величина А разная. Меньше всего величина работы выхода у щелочных металлов, например, для цезия (Cs) А = 1,81 эВ. У цинка, который использовался в опытах Столетова, А = 4,24 эВ. Фотоны поглощаются поодиночке (если интенсивность света не достигает очень больших значений). Энергия фотона hv частично расходуется на работу выхода, оставшаяся часть (mv2max)/2 уносится электроном,
Таким образом
Это и есть уравнение Эйнштейна для фотоэффекта. Если в этом уравнении заменить (mv2max)/2 на еUзад (см. (3.1)), то уравнение Эйнштейна будет иметь следующий вид:

Из последней формулы видно, что величина задерживающего напряжения Uзад прямо пропорциональна частоте света. Из уравнения Эйнштейна для фотоэффекта (3.3) следует, что если энергия фотона hv меньше работы выхода А, то фотоэффект невозможен. Граничная частота определяется равенством:

здесь vкр - красная граница фотоэффекта.
Соответствующая частоте vкр длина волны также называется красной границей фотоэффекта, т.к. v = c/λ , то для λкр имеем:

Название "красная граница" связано с тем, что длинноволновая часть видимого спектра, для которой максимальна длина волны λ и минимальна энергия фотонов, имеет красный цвет.
Ядерная модель атома.
Результаты квантово-механического рассмотрения поведения электрона в водородоподобном атоме.
Излучение и поглощение энергии атомами и молекулами.
Большие успехи в исследовании строения атомов были достигнуты в опытах английского ученого Эрнеста Резерфорда по рассеянию α-частиц при прохождении через тонкие слои вещества. В этих опытах узкий пучок α-частиц, испускаемых радиоактивным веществом, направлялся на тонкую золотую фольгу. За фольгой помещался экран, способный светиться под ударами быстрых частиц. Было обнаружено, что большинство α частиц отклоняется от прямолинейного распространения после прохождения фольги, т. е. рассеивается, а некоторые α-частицы вообще отбрасываются назад. Рассеяние α-частиц Резерфорд объяснил тем, что положительный заряд не распределен равномерно в шаре радиусом 10^(-10)м, как предполагали ранее, а сосредоточен в центральной части атома — атомном ядре. При прохождении около ядра α-частица, имеющая положительный заряд, отталкивается от него, а при попадании в ядро — отбрасывается в противоположном направлении. Так ведут себя частицы, имеющие одинаковый заряд, следовательно, существует центральная положительно заряженная часть атома, в которой сосредоточена значительная масса атома. Расчеты показали, что для объяснения опытов нужно принять радиус атомного ядра равным примерно 10^(-15) м.
Резерфорд предположил, что атом устроен подобно планетарной системе. Суть модели строения атома по Резерфорду заключается в следующем: в центре атома находится положительно заряженное ядро, в котором сосредоточена вся масса, вокруг ядра по круговым орбитам на больших расстояниях вращаются электроны (как планеты вокруг Солнца). Заряд ядра совпадает с номером химического элемента в таблице Менделеева.
Атом водорода состоит из положительно заряженных протона Р и одного электрона е.
n - главное квантовое число; n=1,2,3…; ℓ- орбитальное квантовое число; l=1,2,3…(n-1); m- магнитное квантовое число m=-1,…,0,…,1; J-спиновое квантовое число J=+1/2;-1/2
В состоянии покоя е находится на нижнем уровне. Поглощая W, е переходит на более высокий уровень (переходит в возбужденное состояние).
Время жизни е в возбужд. состоянии - 10-8с, после чего е переходит на уровень ниже.
Возвращение на предыдущий уровень сопровождается излучением фотонов с определенным количеством энергии.
Основные серии переходов: 1) Лаймана (n=1), 2) Бальмера (n=2), 3) Пашена (n=3).
Второй закон термодинамики.
Второй закон термодинамики — физический принцип, накладывающий ограничение на направление процессов, которые могут происходить в термодинамических системах.
Второй закон термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.
1.1
Механическое движение
Механическое движение-это процесс изменения положения тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условное принятое за неподвижное- тело отсчета.
Тело отсчета -это тело, относительно которого определяется положение другого тела.
Система отсчета -это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Траектория движения
Траектория движения тела -это непрерывная линия, которую описывает движущееся тело(рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Пройденный путь
Пройденный путь -скалярная величина, равная длине дуги траектории, пройденной телом за некоторое время.
Перемещение
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением, векторная величина.
Средняя и мгновенная скорости движения.Направление и модуль скорости.
Скорость- физическая величина, которая характеризует быстроту изменения координаты.
Средняя скорость движения - это физическая величина, равная отношению вектора перемещения точки к интервалу времени, за которое это перемещение произошло. Направление вектора средней скорости совпадает с направлением вектора перемещения ∆ S
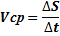
Мгновенная скорость -это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени ∆ t . Вектор мгновенной скорости направлен по касательной к траектории. Модуль равен первой производной пути по времени.
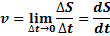
Формула пути при равноускоренном движении.
Равноускоренное движение -это движение, при котором ускорение постоянно по модулю и направлению.
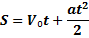
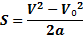
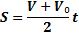
1.2.
Ускорение движения
Ускорение движения- векторная физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.
Дата: 2019-07-24, просмотров: 350.