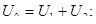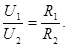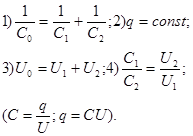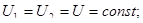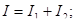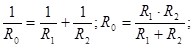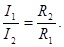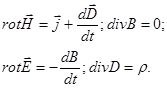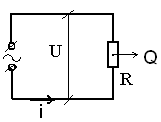
Рис.44
Анализируем с помощью трех методов: 1) векторных диаграмм; 2) графического; 3) аналитического.
Определение активного сопротивления:
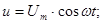 (90)
(90)
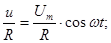 (91)
(91)
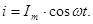 (92)
(92)
Исходя из (90) и (92) 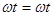 - фазы тока и напряжения совпадают, т.е.
- фазы тока и напряжения совпадают, т.е. 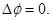
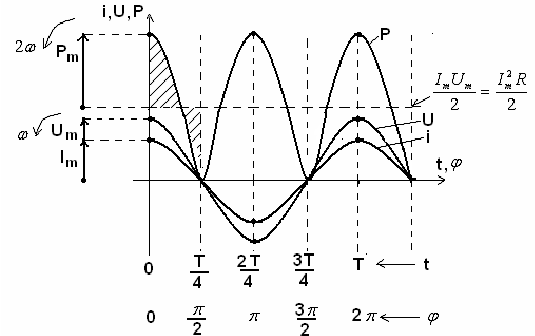
Рис.45
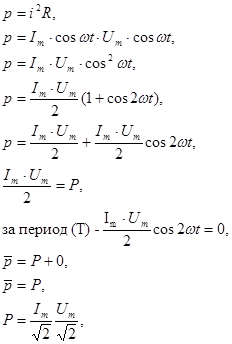
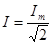 - действующее значение тока, (93)
- действующее значение тока, (93)
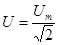 - действующее значение напряжения, (94)
- действующее значение напряжения, (94)
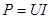 - активная мощность. (95)
- активная мощность. (95)
Активная мощность в цепи переменного тока определяется так же, как в цепи постоянного тока.
Конденсатор в цепи переменного тока.
Постоянный ток не проходит через конденсатор.
Переменный ток проходит через конденсатор за счет его перезарядки.
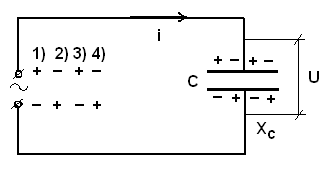
Рис.46
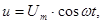 (96)
(96)
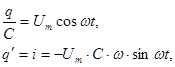
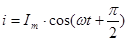 . (97)
. (97)
Ток опережает напряжение на 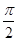 , т.к., чтобы на конденсаторе появилось напряжение, надо, чтобы в цепи протек электрический ток.
, т.к., чтобы на конденсаторе появилось напряжение, надо, чтобы в цепи протек электрический ток. 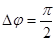 .
.
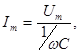 (98)
(98)
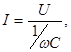 (99)
(99)
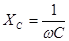 - емкостное сопротивление, (100)
- емкостное сопротивление, (100)
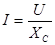 - закон Ома. (101)
- закон Ома. (101)
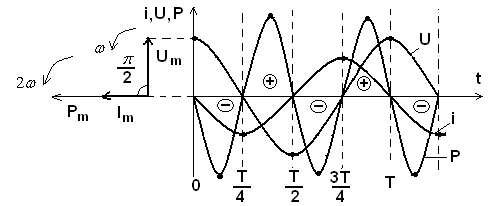
Рис.47
Средняя мощность 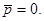
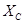 - реактивная нагрузка.
- реактивная нагрузка.
5.3. Катушка индуктивности в цепи переменного тока.
«Индуктивность» оказывает сопротивление переменному току, а постоянный ток «индуктивность» не замечает.
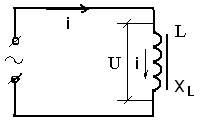
Рис.48
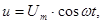 (102)
(102)
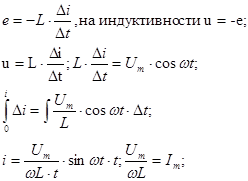
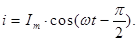 (103)
(103)
Ток(103) отстаёт от напряжения(102) на угол 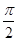 , т.к., чтобы по L протек ток, надо, чтобы на L сначала было напряжение, т.е.
, т.к., чтобы по L протек ток, надо, чтобы на L сначала было напряжение, т.е. 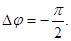
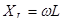 - индуктивное сопротивление; (104)
- индуктивное сопротивление; (104)
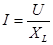 - закон Ома; (105)
- закон Ома; (105)
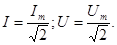 - действующие значения тока и напряжения. (106)
- действующие значения тока и напряжения. (106)
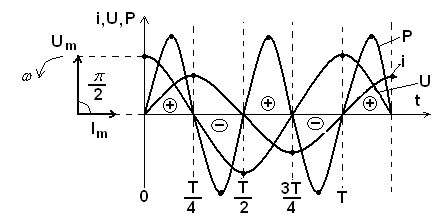
Рис.49
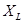 - реактивная нагрузка;
- реактивная нагрузка;
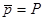 - реактивная мощность, при чисто индуктивной нагрузке ее среднее значение равно нулю.
- реактивная мощность, при чисто индуктивной нагрузке ее среднее значение равно нулю.
Лекция 15
5.4. Цепь переменного тока с R , L и С.
Так было, когда мы U брали за основу. Здесь все значения максимальные. От них можно перейти к действующим.
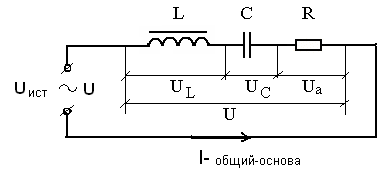
Рис.50
При последовательном соединении 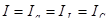
Основа – U, Основа – Iобщий , складывая 1), 2) и 3)
так было ранее так должно быть получим:
сейчас
( по схеме рис.50)
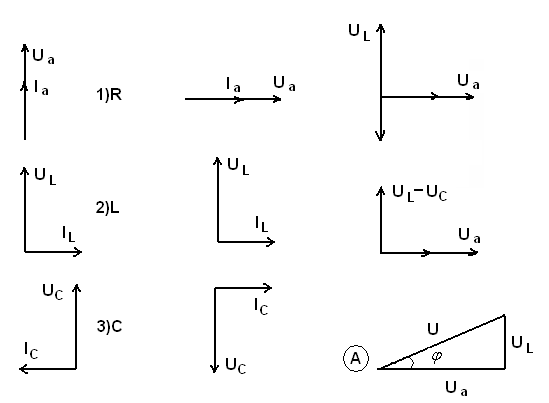
Рис.51
( А) – треугольник напряжений. Можно найти стороны. φ – сдвиг фаз между током в цепи (i) и напряжением(u) в источнике (розетке). 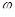 <
< 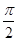 .
.
Если в треугольнике (А) стороны поделить на R, то получим (Б) – треугольник сопротивлений, подобный А, из которого получим закон Ома для цепи переменного тока с R, L и С.
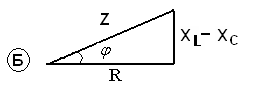
Рис.52
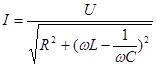 , или (107)
, или (107)
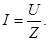 (108)
(108)
Если у треугольника (А) стороны умножить на I ,то получим треугольник мощностей (В).
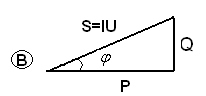
Рис. 53
Здесь Р – активная мощность (Вт),
Q – реактивная мощность (ВАр),
S – полная мощность (ВА).
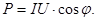 (109) cosφ – коэффициент мощности.
(109) cosφ – коэффициент мощности.
Добиваются снижения φ и увеличения cosφ – на предприятиях.
Резонанс в электрической цепи.
Если добиться, чтобы 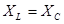 , то φ будет рано нулю и в цепи наблюдается резонанс. Чтобы добиться резонанса можно менять ω, L и С.
, то φ будет рано нулю и в цепи наблюдается резонанс. Чтобы добиться резонанса можно менять ω, L и С.
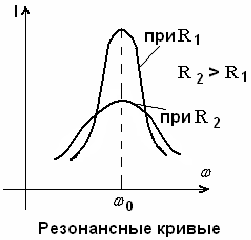
Рис.55
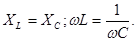
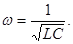 (110)
(110)
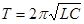 - формула Томсона. (111)
- формула Томсона. (111)
Здесь L и С обмениваются энергией. Мощность – только активная. 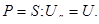
Обобщения теории Максвелла.
В 60-х годах 19-века Д.К.Максвелл, основываясь на идеях Фарадея об электрическом и магнитном полях, обобщил законы, установленные экспериментальным путем, и разработал теорию единого электромагнитного поля.
Математическим выражением теории Максвелла служат четыре уравнения Максвелла, которые принято записывать в двух формах: интегральной и дифференциальной. Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей. Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. Дифференциальные уравнения получают из интегральных с помощью теоремы Гаусса и теоремы Стокса.
6.1. Система уравнений Максвелла в дифференциальной форме:

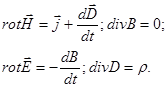
6.2. Уравнения Максвелла в интегральной форме.
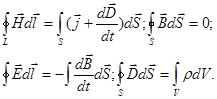

Связь величин:
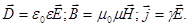
Если поля стационарны, то Е = const и В = const.
Уравнения Максвелла примут вид:
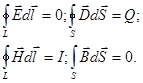
6.3. Уравнение волны:
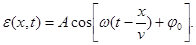
Резерв времени – 4 часа.
Формулы
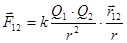 ; ;
| 
|  . .
|
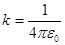 . .
| 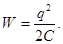
| 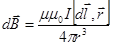 . .
|
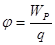 ; ; 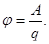
| 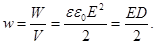
| 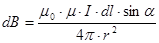 . .
|
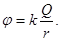
| 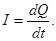
| 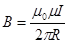 . .
|
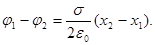
| 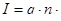 v v 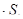
| 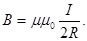
|
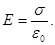
| 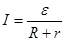 . .
| 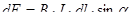 . .
|
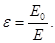
| 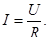
| 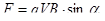
|
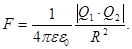
| 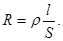
| 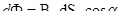
|
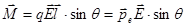 . .
| 
| 
|
 ; ; 
| 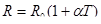 . .
| 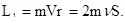
|
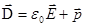 ; ; 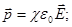
| 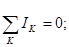 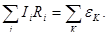
| 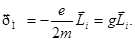
|
| 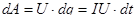 . .
| 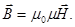
|
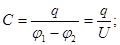
| 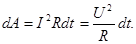
| 
|
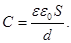
| 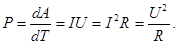
| 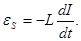
|
| Параллельное соединение конденсаторов:
| Законы последовательного соединения проводников: 1) 2) 4) | 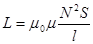 . .
|
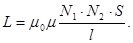
| ||
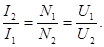
| ||
| Последовательное соединение конденсаторов:
| Законы параллельного соединения проводников: 1) 2) 3) 4) | 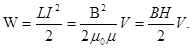
|
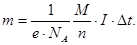
| ||
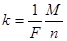 . .
| ||
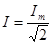 ; ; 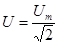 . .
| 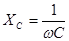 ; ; 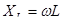 . .
| 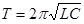 . .
|
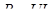 . .
| 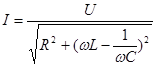 . .
| Уравнения Максвелла в дифференциальной форме:
|
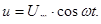
| 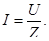
| |
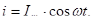
| 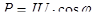
|
Основная литература:
1. Савельев И.В. Курс общей физики т. 2, М.:Наука,1999,340с.
2.Трофимова Т.И. Курс физики: учебное пособие для вузов – М.: «Академия»,2007,560с.
3. Детлаф А.А.,Яворский Б.М. Курс физики: учебное пособие для вузов – М.: «Высшая школа»,2001,718с.
Дата: 2019-07-24, просмотров: 314.
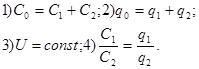
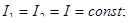
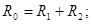 3)
3)