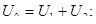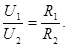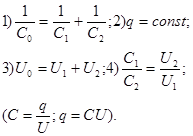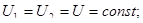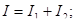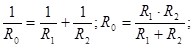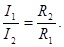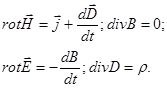Физика.
Курс лекций, II семестр, 34 часа
III, IV. Электричество и магнетизм
| Оглавление Лекция 1. 1. Электростатика. 1.1. Электрический заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Потенциал. Разность потенциалов. | 4 4 |
| Лекция 2. 1.2. Диэлектрики в электростатическом поле. Диполь. Дипольный момент. Вектор поляризации. Электростатическая теорема Гаусса. Вектор электрической индукции. Уравнение Пуассона. Условия на границе раздела двух сред. | 7 |
| Лекция 3. 1.3. Проводники в электростатическом поле. Распределение зарядов на проводнике. Электрическое поле внутри и вне проводника. Электростатическая защита. | 10 |
| Лекция 4. 1.4. Электрическая емкость. Конденсаторы. Энергия электрического поля. Плотность энергии электростатического поля. | 12 |
| Лекция 5. 2. Постоянный электрический ток. 2.1. Сила и плотность тока. Закон Ома для участка цепи и замкнутого контура. Сторонние силы. Электродвижущая сила. Закон Ома в дифференциальной форме. | 14 14 |
| Лекция 6. 2.2. Разветвление электрической цепи. Правила Кирхгофа. 2.3. Работа и мощность электрического тока. Закон Джоуля-Ленца. Превращение энергии в электрических цепях. | 17 19 |
| Лекция 7. 3.Магнитное поле. 3.1. Магнитное поле тока. Законы Био-Савара-Лапласа и Ампера. Сила Лоренца. Вектор магнитной индукции. Поток вектора магнитной индукции через замкнутую поверхность. Теорема о циркуляции вектора магнитной индукции. | 21 |
| Лекция 8. Магнитное поле прямого тока. Магнитное поле в центре кругового проводника с током. Взаимодействие двух проводников. Сила Лоренца. Поток вектора магнитной индукции. | 23 |
| Лекция 9. 3.2. Магнитные свойства вещества. Молекулярные токи. Диа -, пара- и ферромагнетики. Вектор намагниченности. Магнитная восприимчивость и магнитная проницаемость. Представление о ядерном магнитном резонансе и электронном парамагнитном резонансе. | 26 |
| Лекция 10. 3.3. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Индуктивность. Самоиндукция. Плотность энергии магнитного поля. Взаимоиндукция. Трансформатор. | 29 |
| Лекция 11. 4. Электронные и ионные явления. 4.1. Электропроводность твердых тел. Зависимость сопротивления металлов от температуры. Сверхпроводимость. Полупроводники. Эффект Холла. Электронная и дырочная проводимости, p – n переходы. Диоды, транзисторы, интегральные схемы. | 33 |
| Лекция 12. 4.2. Токи в газах. Ионизация газов. Газоразрядная плазма. Движение заряженных частиц в электрических и магнитных полях. Циклотрон. Масс-спектрометр. Электронный микроскоп. | 36 |
| Лекция 13. 4.3. Токи в электролитах, Закон Фарадея. Электролитическая диссоциация. Химические источники тока. 4.4. Контактные явления. Работа выхода электронов. Контактная разность потенциалов. Термоэлектронная эмиссия. | 38 39 |
| Лекция 14. 5. Переменный электрический ток. | |
| Лекция 15. 5.4. Цепь переменного тока с R, L и С. 6. Обобщения теории Максвелла. | 39 |
| Формулы. | 47 |
Лекция 1.
Электростатика
1.1. (2 часа). Электрический заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Потенциал. Разность потенциалов.
Существуют два рода зарядов: 1)положительные и 2)отрицательные. Положительные заряды образуются на стеклянной палочке, потертой о шелк, а отрицательные заряды образуются на каучуковой палочке, потертой о мех. Опытным путем (1910 – 1914) американский физик Р.Милликен показал, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда ( 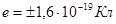 ). Электрон (
). Электрон ( 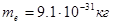 ) и протон (
) и протон ( 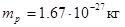 ) являются соответственно носителями элементарных отрицательного и положительного зарядов. Все тела способны электризоваться, т.е. получать избыточный электрический заряд. Электризация может осуществляться различными способами: соприкосновением (трением), электростатической индукцией (наведением) и др. При электризации электризуются оба тела: одно – положительно, другое – отрицательно. Положительная электризация объясняется недостатком электронов в теле, отрицательная – их избытком. В природе выполняется закон сохранения зарядов. В зависимости от концентрации свободных зарядов все вещества делятся на 1)проводники, 2)диэлектрики и 3)полупроводники. Единицей электрического заряда является кулон (Кл). Кулон – это такой заряд, который проходит через поперечное сечение проводника при силе тока 1А за время 1с.
) являются соответственно носителями элементарных отрицательного и положительного зарядов. Все тела способны электризоваться, т.е. получать избыточный электрический заряд. Электризация может осуществляться различными способами: соприкосновением (трением), электростатической индукцией (наведением) и др. При электризации электризуются оба тела: одно – положительно, другое – отрицательно. Положительная электризация объясняется недостатком электронов в теле, отрицательная – их избытком. В природе выполняется закон сохранения зарядов. В зависимости от концентрации свободных зарядов все вещества делятся на 1)проводники, 2)диэлектрики и 3)полупроводники. Единицей электрического заряда является кулон (Кл). Кулон – это такой заряд, который проходит через поперечное сечение проводника при силе тока 1А за время 1с.
Закон Кулона. Закон взаимодействия неподвижных точечных зарядов экспериментально установлен в 1785 г. Ш.Кулоном с помощью крутильных весов, подобных тем, которые использовались Г.Кавендишем для определения гравитационной постоянной ( ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет). Точечный заряд – это такой заряд, который сосредоточен на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других зарядов. Сила взаимодействия (F) между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна величинам этих зарядов (Q1 и Q2) и обратно пропорциональна квадрату расстояния между ними 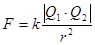 (1) в векторной форме:
(1) в векторной форме: 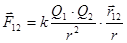 ; (2) где
; (2) где 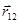 - радиус вектор, соединяющий заряд
- радиус вектор, соединяющий заряд 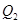 с зарядом
с зарядом 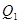 ;
; 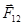 - действует на заряд 1.
- действует на заряд 1. 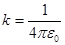 - коэффициент пропорциональности,
- коэффициент пропорциональности, 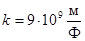 ;
; 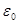 -электрическая постоянная вакуума,
-электрическая постоянная вакуума, 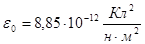 или (
или ( 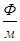 ), фарад – единица электроемкости. Точность закона проверена в большом интервале расстояний.
), фарад – единица электроемкости. Точность закона проверена в большом интервале расстояний.
Напряженностью электростатического поля в данной точке называется величина, равная отношению силы, действующей на положительный пробный заряд, помещенный в данную точку поля, к величине этого заряда.
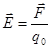 ; (3) для точечного заряда
; (3) для точечного заряда 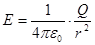 . (4) Вектор
. (4) Вектор 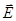 направлен в ту же сторону, что и сила.
направлен в ту же сторону, что и сила.
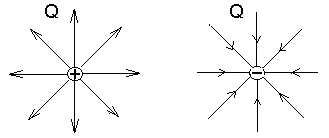
Рис.1
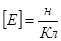 ; Линия напряженности – линия, касательная к которой в каждой точке совпадает с направлением напряженности в данной точке.
; Линия напряженности – линия, касательная к которой в каждой точке совпадает с направлением напряженности в данной точке.
Напряженность поля от нескольких зарядов равна векторной (геометрической) сумме напряженностей, созданных отдельными зарядами.
Поток вектора напряженности: 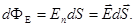
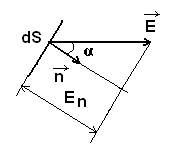
Единица потока вектора напряженности электрического поля - вольт·метр (В·м).
Потенциал электростатического поля.
Поля, в которых работа силы (созданной полем) по замкнутой траектории равна нулю называются потенциальными. Это – электростатическое и гравитационное поля.
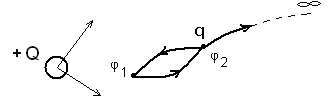
Рис.2
Определение I : Потенциалом поля в данной точке называется величина, равная отношению потенциальной энергии заряда в этой точке, к величине этого заряда.
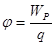 . (5)
. (5)
Определение II : Потенциалом поля в данной точке называется величина, равная отношению работы по перемещению положительного пробного заряда из данной точки поля в бесконечность, к величине этого заряда.
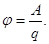 (6)
(6)
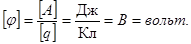
Лекция 2
1.2. (2 часа) Диэлектрики в электростатическом поле. Диполь. Дипольный момент. Вектор поляризации. Электростатическая теорема Гаусса. Вектор электрической индукции. Уравнение Пуассона. Условия на границе раздела двух сред.
- Два вида диэлектриков:
( 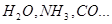 ) (
) ( 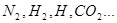 )
)
1. Полярные – это такие диэлектрики, 2. Неполярные – это такие диэлектрики,
у которых центры положительных и у которых центры положительных и от-
отрицательных зарядов внутри моле- рицательных зарядов совмещены (ε <3).
кул разделены (ε >3).


противоположных по знаку электри- совмещен с центром положительного за-
ческих зарядов. ряда (ядра).
2(а). 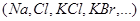 Эту группу составляют вещества, молекулы которых имеют ионное строение (ионные кристаллы). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток (разного знака). (ε >3).
Эту группу составляют вещества, молекулы которых имеют ионное строение (ионные кристаллы). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток (разного знака). (ε >3).
Поляризация диэлектриков.
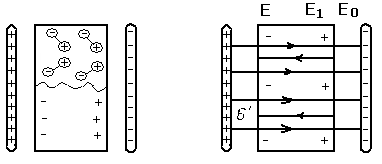
Рис.5
В полярных диэлектриках диполи поворачиваются, а в неполярных и ионных – заряды смещаются.
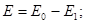
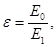 (12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
(12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
Закон Кулона:
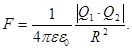 (13)
(13)
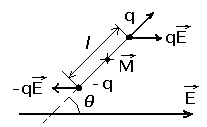
Рис.6
Электрический момент диполя: 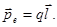 (14)
(14)
Дипольный момент: 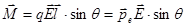 (15) или:
(15) или: 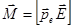 - этот вектор направлен перпендикулярно плоскости векторов
- этот вектор направлен перпендикулярно плоскости векторов 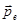 и
и 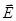 , так что из конца вектора
, так что из конца вектора 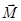 вращение от
вращение от 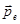 к
к 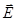 по кратчайшему пути видно происходящим против часовой стрелки.
по кратчайшему пути видно происходящим против часовой стрелки.
Поляризованностью называют дипольный момент единицы объема диэлектрика:
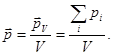 (16)
(16)
Для большинства диэлектриков (за исключением сегнетодиэлектриков) поляризованность линейно зависит от напряженности поля (Е). Если диэлектрик изотропный и 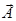 не слишком велико, то
не слишком велико, то
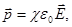 (17) где χ – диэлектрическая восприимчивость вещества:
(17) где χ – диэлектрическая восприимчивость вещества:
χ + 1 = ε, (18) величина безразмерная, причем χ >0. Поляризованность проявляется образованием на поверхности диэлектрика связанных зарядов. Поверхностная плотность ( 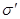 ) связанных зарядов равна поляризованности (р).
) связанных зарядов равна поляризованности (р). 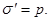 Вектор электрического смещения (поляризации) для электрически изотропной среды:
Вектор электрического смещения (поляризации) для электрически изотропной среды:
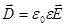 (19) или
(19) или 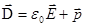 . (20)
. (20)
Единица электрического смещения - 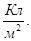 Вектором
Вектором 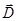 описывается электрическое поле, созданное связанными зарядами.
описывается электрическое поле, созданное связанными зарядами.
Поляризацией диэлектрика называется процесс ориентации диполей или появление под действием внешнего электрического поля ориентированных по полю диполей.
Вектор 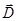 аналогично
аналогично 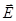 изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
Для произвольной замкнутой поверхности S поток вектора 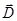 сквозь эту поверхность:
сквозь эту поверхность:
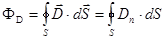 , (21) где
, (21) где 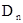 - проекция
- проекция 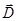 на нормаль
на нормаль 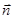 к площадке dS .
к площадке dS .
Теорема Гаусса для электростатического поля в диэлектрике:
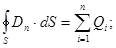 (22) или упрощенно
(22) или упрощенно 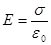 или D = σ.
или D = σ.
Для электростатического поля в вакууме дифференциальное уравнение, называемое уравнением Пуассона:
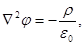 (23) где оператор Лапласа:
(23) где оператор Лапласа:
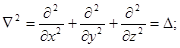 (24) ρ – объемная плотность заряда. В среде
(24) ρ – объемная плотность заряда. В среде 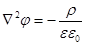 , φ – потенциал поля.
, φ – потенциал поля.
Если в среде нет свободных зарядов, то 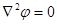 - уравнение Лапласа.
- уравнение Лапласа.
Условия на границе раздела двух сред:
ε2 > ε1
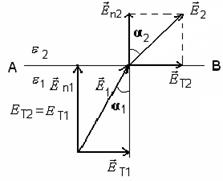
Рис.7
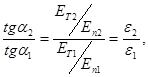 отсюда
отсюда 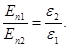 (25)
(25)
На границе двух сред нет свободных зарядов, тогда Еn2 < En1, т.к ε2 > ε1.
Лекция 3 .
1.3.(2часа) Проводники в электростатическом поле. Распределение зарядов на проводнике. Электрическое поле внутри и вне проводника. Электростатическая защита.
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. Если поле внутри проводника не было бы равно нулю, то под действием этого поля заряды пришли бы в движение без внешнего источника, что противоречит закону сохранения энергии. Равенство нулю электрического поля внутри проводника приводит к тому, что потенциал поля внутри проводника одинаков (φ = const). Поверхности, которые имеют одинаковый потенциал, называются эквипотенциальными. Отсюда следует, что в любой точке проводника любой формы в каждой его точке вектор напряженности поля на внешней поверхности перпендикулярен к этой поверхности. Если бы было не так, то под действием составляющей напряженности вдоль этой поверхности заряды пришли бы в движение, что противоречит равновесному распределению зарядов.
Если проводнику сообщить некоторый заряд, то он распределится по поверхности проводника, внутри же проводника зарядов так же не будет.
Взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью σ зарядов на его поверхности в соответствии с теоремой Гаусса будет:
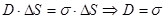 (26)
(26)
или 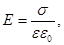 (27) где ε – диэлектрическая проницаемость вещества.
(27) где ε – диэлектрическая проницаемость вещества.
Согласно этой формулы Е и σ связаны вблизи проводника любой формы. Из формулы 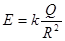 и формулы (27) вытекает, что плотность зарядов и напряженность поля на одном и том же проводнике там больше, где кривизна поверхности (1/R) больше, или R меньше.
и формулы (27) вытекает, что плотность зарядов и напряженность поля на одном и том же проводнике там больше, где кривизна поверхности (1/R) больше, или R меньше.
Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряд придут в движение и будут двигаться до поверхности проводника.
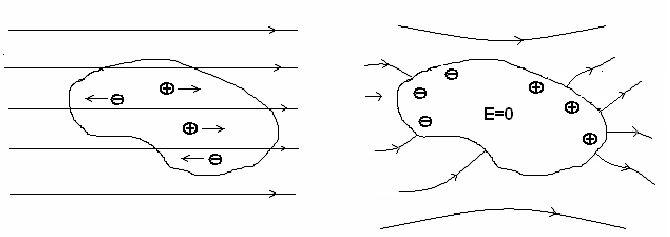
Рис.8
Эти заряды называются индуцированными. Напряженность внутри проводника будет равна нулю. Явление образования индуцированных зарядов называется электростатической индукцией. По формуле (26) электрическое смещение вблизи проводника численно равно поверхностной плотности смещенных электрических зарядов, поэтому вектор 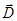 получил название вектора электрического смещения. Применение явления – электростатическая защита – густая металлическая сетка (экранирование приборов, установок, людей).
получил название вектора электрического смещения. Применение явления – электростатическая защита – густая металлическая сетка (экранирование приборов, установок, людей).
Электростатический генератор – предназначен для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт.
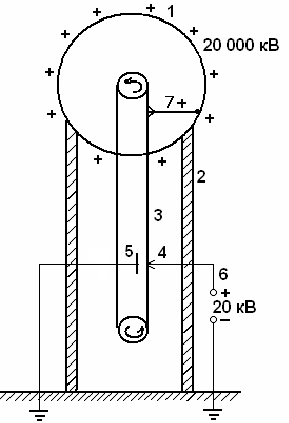
Рис.9. 1 – шарообразный полый проводник,
2 – изоляторы, 3 – лента из прорезиненной ткани,
4 – система остриев, 5 – заземленная пластина,
6 – источник высокого напряжения,
7 – кисточковый съемник зарядов.
Лекция 4.
1.4. (2часа). Электрическая емкость. Конденсаторы. Энергия электрического поля. Плотность энергии электростатического поля.
Понятие электроемкости уединенного проводника такое же как и для двух проводников. В этом случае электроемкостью двух проводников называется отношение заряда на одном из проводников к разности потенциалов между этими проводниками.
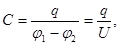 (28) где С – емкость;
(28) где С – емкость;
q – заряд;
U – разность потенциалов.
Единицы электроемкости
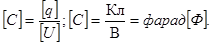
В радио: В учебниках:
1 мкФ = 10-6Ф мФ, мкФ, нФ, nФ
1nФ = 10-12Ф
Опыт
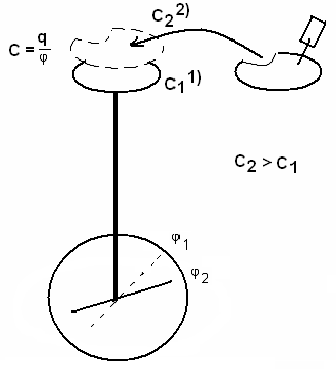
Рис.10
Электроемкость шара.
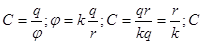 ~ r .
~ r .
Емкость земного шара 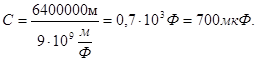 Емкость Солнца: 0,2Ф.
Емкость Солнца: 0,2Ф.
Конденсаторы – устройства для накапливания электрических зарядов, изобретались как устройства, обладающие большой емкостью.
Конденсатор – устройство, состоящее из двух пластин, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами пластин.
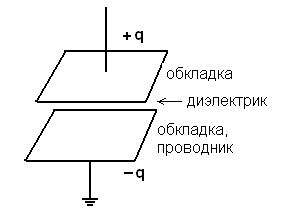
Рис.11 Зарядка конденсатора
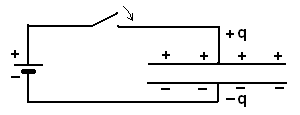
Рис.12
Под зарядом конденсатора понимают заряд одной из его пластин.
Первый конденсатор – лейденская банка.
Электроемкость плоского конденсатора:
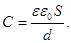 (29)
(29)
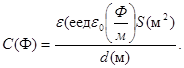 (Объяснение зависимости С от S и d).
(Объяснение зависимости С от S и d).
Измерение диэлектрической проницаемости
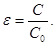 (30)
(30)
Электроемкость шарового и цилиндрического конденсатора при r >> d определяется по формуле (16).
Плотность тока.
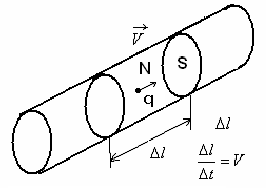
Рис.15
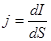 - плотность тока; (36)
- плотность тока; (36)
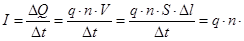 v
v 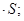
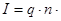 v
v 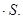 (37)
(37)
v 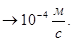 Из формул (36) и (37) получим
Из формул (36) и (37) получим
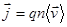 . (38)
. (38)
Сторонние силы – это силы любого неэлектрического происхождения, выполняющие функцию разделения зарядов внутри источника тока. Природа сторонних сил: 1) в электрических генераторах – это магнитные силы, 2) в гальванических элементах (Вольта) – химические силы (медь, цинк), цинк – «-», раствор – «+». Роль источника тока в электрической цепи, образно говоря, такая же, как роль насоса в гидравлической системе.
Электродвижущая сила. ЭДС в замкнутом контуре представляет собой отношение работы сторонних сил при разделении зарядов внутри источника тока к величине этого заряда (одного знака). Но работа сторонних сил затрачивается на работу электрического поля вдоль замкнутого контура 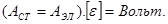 При расчете электрических цепей ЭДС считается положительной, если при обходе контура движение внутри источника осуществляется от его «минуса» к «плюсу».
При расчете электрических цепей ЭДС считается положительной, если при обходе контура движение внутри источника осуществляется от его «минуса» к «плюсу».
Закон Ома для полной цепи.
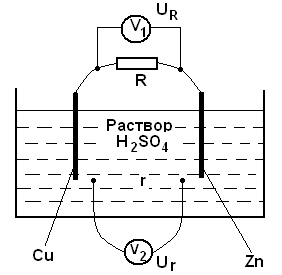
Рис.16
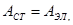
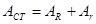 ,
,
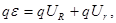
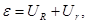
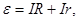
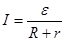 - закон Ома для полной цепи, здесь (39)
- закон Ома для полной цепи, здесь (39)
R – внешнее сопротивление;
r – внутреннее сопротивление.
Закон Ома для участка цепи.
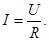 (40)
(40)
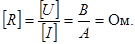
R – сопротивление, Ом;
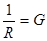 - проводимость;
- проводимость; 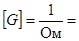 сименс (См).
сименс (См).
Удельное сопротивление: ρ;
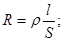 (41)
(41)
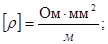
В «Си» 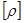 =Ом·м; ρ(меди)=
=Ом·м; ρ(меди)= 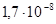 Ом·м.
Ом·м.
Лекция 6.
2.2.(1 час) Разветвление электрической цепи. Правила Кирхгофа.
Непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.) довольно сложен. Эта задача более просто решается с помощью двух правил Кирхгофа (немецкий физик, 1824 – 1887). Любая точка разветвления цепи, в которой сходятся не менее трех проводников с током, называется узлом. При этом ток, входящий в узел считается положительным, а ток, выходящий из узла – отрицательным.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
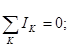 (44) или непосредственно по рисунку 17:
(44) или непосредственно по рисунку 17:
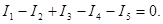
Это правило вытекает из закона сохранения заряда.
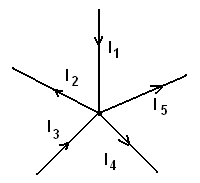
Рис.17
Второе правило Кирхгофа: в любом замкнутом контуре (произвольно выбранном в разветвленной электрической цепи) алгебраическая сумма произведений сил токов 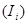 на сопротивление
на сопротивление 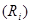 соответствующих участков этого контура равна алгебраической сумме ЭДС
соответствующих участков этого контура равна алгебраической сумме ЭДС 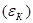 , встречающихся в этом контуре:
, встречающихся в этом контуре:
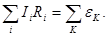 (45)
(45)
Если направление тока (I) совпадает с направлением обхода, то ток положителен. Если направление обхода от «минуса» к «плюсу» источника, то ЭДС положительна и наоборот.
Пример:
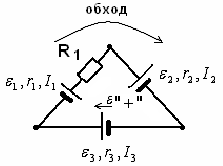
Рис.18
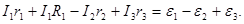
При расчете сложных цепей постоянного тока используют следующий алгоритм:
1. Выбрать произвольное направление токов на всех участках цепи; действительные направления токов определятся после решения задачи; если искомый ток получится положительным, то его направление было выбрано правильным, если отрицательным, то его истинное направление противоположно выбранному.
2. Выбрать произвольно направление обхода контура и строго придерживаться его. Записать произведения токов на сопротивления с учетом знаков и приравнять их сумме ЭДС. Составить уравнения по первому правилу Кирхгофа.
3. По этапам 1 и 2 составить столько уравнений, чтобы их число было равно числу искомых величин. В систему уравнений должны входить все сопротивления и ЭДС цепи.
В качестве примера рассмотрим схему измерительного моста Уинстона (английский физик, 1802 – 1875). Используется для определения неизвестных сопротивлений.
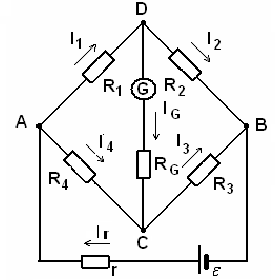 Рис.19
Рис.19
Сопротивления 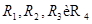 образуют его «плечи». Между точками А и В моста включена батарея с ЭДС ε и сопротивлением r, между точками С и Д включен гальванометр с сопротивлением
образуют его «плечи». Между точками А и В моста включена батарея с ЭДС ε и сопротивлением r, между точками С и Д включен гальванометр с сопротивлением 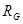 . Для узлов А,В, и С, применяя первое правило Кирхгофа, получим:
. Для узлов А,В, и С, применяя первое правило Кирхгофа, получим: 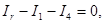
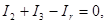
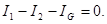 (1)
(1)
Для контуров АСВА, АСДА и АВДС можно записать: 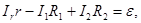
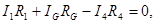
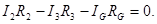 (2)
(2)
Если известны все сопротивления и ЭДС, то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления 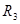 и
и 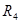 можно добиться, чтобы ток через гальванометр был равен нулю
можно добиться, чтобы ток через гальванометр был равен нулю 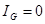 , тогда из (1) получим
, тогда из (1) получим 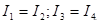 (3). Тогда из (2) получим:
(3). Тогда из (2) получим: 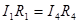 и
и 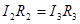 (4). Из (3) и (4) получим
(4). Из (3) и (4) получим 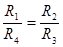 или
или 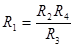 (5). Тогда в случае равновесного моста
(5). Тогда в случае равновесного моста 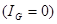 при определении неизвестного (искомого) сопротивления
при определении неизвестного (искомого) сопротивления 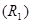 ЭДС батареи, сопротивление батареи и гальванометра роли не играют.
ЭДС батареи, сопротивление батареи и гальванометра роли не играют.
На практике используют реохордный мостик Уинстона, где сопротивления 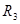 и
и 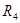 представляют собой одну длинную проволоку с большим удельным сопротивлением. Тогда формула (5) будет
представляют собой одну длинную проволоку с большим удельным сопротивлением. Тогда формула (5) будет 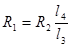 . Длины
. Длины 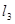 и
и 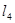 легко измеряются по шкале, а
легко измеряются по шкале, а 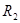 всегда известно.
всегда известно.
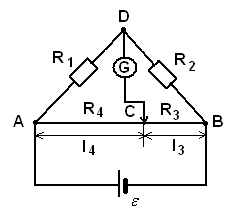
Рис.20
Магнитное поле
3.1 (2часа) Магнитное поле тока. Законы Био-Савара-Лапласа и Ампера. Сила Лоренца. Вектор магнитной индукции. Поток вектора магнитной индукции через замкнутую поверхность. Теорема о циркуляции вектора магнитной индукции.
В пространстве, где протекает электрический ток и находятся постоянные магниты образуется силовое поле, называемое магнитным полем. Название «магнитное поле» возникло при наблюдении ориентации магнитной стрелки под действием этого поля.
Свойства магнитного поля: 1) Магнитное поле создается током (движущимися зарядами); 2) Магнитное поле обнаруживается по действию на электрический ток.
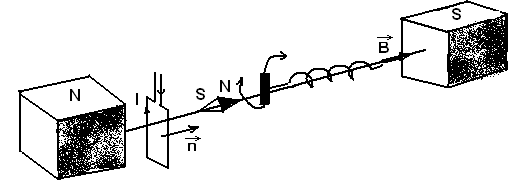
Рис.23
Изучение магнитных полей проводят с помощью 1)рамки стоком, 2)магнитной стрелки. Используют правило буравчика.
За направление магнитного поля принимают направление, в котором устанавливается 1)ось магнитной стрелки от S к N или 2)нормаль к плоскости рамки, определяемая по правилу буравчика (правого винта).
Правило: за положительное направление нормали принимают направление поступательного движения винта, рукоятка которого вращается в направлении тока, протекающего в рамке. Вращающий момент, действующий на рамку: 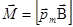 , где
, где 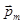 - вектор магнитного момента рамки с током,
- вектор магнитного момента рамки с током, 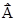 - вектор магнитной индукции. Для плоского контура с током:
- вектор магнитной индукции. Для плоского контура с током: 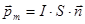 , где S – площадь поверхности контура (рамки),
, где S – площадь поверхности контура (рамки), 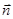 - единичный вектор нормали. (Направления
- единичный вектор нормали. (Направления 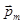 и
и 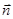 совпадают).
совпадают).
Характеристикой поля может служить магнитная индукция:
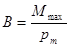 (51)
(51)
Магнитной индукцией поля называется отношение максимального вращающего момента к магнитному моменту, когда нормаль к рамке перпендикулярна направлению поля. Вектор 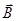 может быть получен по закону Ампера и из выражения для силы Лоренца.
может быть получен по закону Ампера и из выражения для силы Лоренца.
Линии магнитной индукции – линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции. Их направление определяется с помощью рамок с током и с помощью магнитных стрелок.
Линии магнитной индукции можно проявить с помощью магнитных стрелок. Свойства линий магнитной индукции: они всегда замкнуты, они нигде не пересекаются, они расположены там гуще, где магнитное поле сильнее, для постоянных магнитов они выходят с из северного полюса и входят в южный.
Магнитное поле – вихревое поле. Магнитных зарядов, подобных электрическим, нет.
Магнитные свойства вещества объясняются циркуляционными токами, протекающими в атомах веществ, они создают свое магнитное поле и могут поворачиваться по отношению к внешнему полю, полю макротоков. Магнитное поле макротоков описывается вектором напряженности магнитного поля 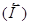 .
.
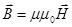 , (52)
, (52)
где 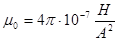 - магнитная постоянная,
- магнитная постоянная,
μ – магнитная проницаемость среды, ед, безразмерная величина, она показывает во сколько раз магнитное поле в среде больше чем вне среды,
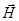 - вектор напряженности магнитного поля,
- вектор напряженности магнитного поля, 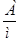 ,
,
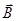 - индукция магнитного поля,
- индукция магнитного поля, 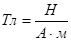 .
.
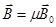 , (53)
, (53)
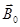 - индукция магнитного поля вне среды (вакуум),
- индукция магнитного поля вне среды (вакуум),
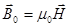 - связь
- связь 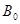 и Н (индукции и напряженности).
и Н (индукции и напряженности).
Закон Био-Савара-Лапласа (французские ученые) получен (рис.22) для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля 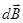 , записывается в виде:
, записывается в виде:
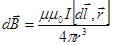 , (54) где
, (54) где 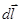 - вектор по модулю равный длине dl провода и совпадающий по направлению с током,
- вектор по модулю равный длине dl провода и совпадающий по направлению с током,
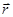 - радиус- вектор проведенный из элемента dl проводника в точку А поля,
- радиус- вектор проведенный из элемента dl проводника в точку А поля,
r  – модуль радиуса –вектора
– модуль радиуса –вектора 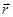 .
.
Направление 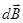 перпендикулярно
перпендикулярно 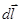 и
и 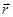 , т.е. перпендикулярно плоскости, в которой они лежат.
, т.е. перпендикулярно плоскости, в которой они лежат.
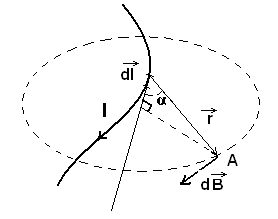
Рис.24
Модуль вектора 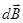 определяется выражением:
определяется выражением:
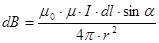 . (55)
. (55)
Для магнитного поля выполняется принцип суперпозиции: вектор магнитной индукции результирующего поля, создаваемого несколькими токами (или их элементами, а также движущимися зарядами) равен векторной сумме магнитных индукций, создаваемых этими токами (или их элементами, а также движущимися зарядами):
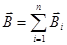 . (56)
. (56)
Расчет характеристик магнитного поля ( 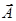 и
и 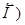 по приведенным формулам в общем случае сложен.. Однако, если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа и принципа суперпозиции позволяет просто рассчитать конкретные поля.
по приведенным формулам в общем случае сложен.. Однако, если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа и принципа суперпозиции позволяет просто рассчитать конкретные поля.
Лекция 8
Рассмотрим два примера:
1. Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины.
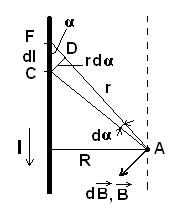
Рис.25
В произвольной точке А, удаленной от оси проводника на расстояние R. Сложение векторов 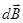 можно заменить сложением их модулей. В качестве постоянной интегрирования выбираем угол α (между
можно заменить сложением их модулей. В качестве постоянной интегрирования выбираем угол α (между 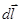 и
и 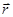 ), выразив через него все остальные величины.
), выразив через него все остальные величины.
Из рисунка:
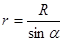 , (57)
, (57)
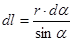 . (58)
. (58)
Подставляя эти величины в (43) закон Био-Савара-Лапласа, получим:

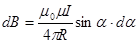 . (59)
. (59)
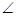 α меняется от 0 до π, поэтому:
α меняется от 0 до π, поэтому:
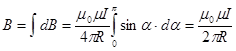 . (60)
. (60)
Лекция 9
3.2.(2часа) Магнитные свойства вещества. Молекулярные токи. Диа -, пара – и ферромагнетики. Вектор намагниченности. Магнитная восприимчивость и магнитная проницаемость. Представление о ядерном магнитном резонансе и электронном парамагнитном резонансе.
Магнитные моменты электронов и атомов. Все вещества, помещенные в магнитное поле, намагничиваются. С точки зрения строения атомов, электрон, движущийся по круговой орбите обладает орбитальным магнитным моментом:
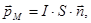 (74) его модуль
(74) его модуль
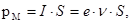 (75) где
(75) где 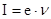 - сила тока,
- сила тока,
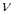 - частота вращения,
- частота вращения,
S – площадь орбиты.
Направление вектора 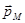 определяется правилом буравчика. Электрон, движущийся по орбите, обладает также механическим моментом импульса
определяется правилом буравчика. Электрон, движущийся по орбите, обладает также механическим моментом импульса 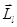 , модуль которого
, модуль которого
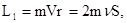 - орбитальный механический момент электрона. (76) где
- орбитальный механический момент электрона. (76) где 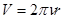 ,
,
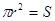 .
.
Направления 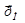 и
и 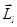 противоположные, т.к. заряд электрона отрицательный. Из (75) и (76) получим
противоположные, т.к. заряд электрона отрицательный. Из (75) и (76) получим
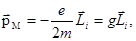 (77) где
(77) где 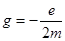 - гиромагнитное отношение. (78)
- гиромагнитное отношение. (78)
Формула справедлива и для некруговых орбит. Экспериментально величину g определили Эйнштейн и де Гааз (1915). Оно оказалось равным 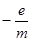 , т.е в два раза большим, чем (78). Тогда было предположено, а в последствии доказано, что кроме орбитальных моментов электрон обладает собственным механическим моментом импульса
, т.е в два раза большим, чем (78). Тогда было предположено, а в последствии доказано, что кроме орбитальных моментов электрон обладает собственным механическим моментом импульса 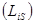 , называемым спином. Спину электрона
, называемым спином. Спину электрона 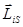 соответствует собственный (спиновый) магнитный момент
соответствует собственный (спиновый) магнитный момент 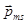 :
: 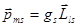 . Величина
. Величина 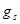 называется гиромагнитным отношением спиновых моментов. Проекция собственного магнитного момента на направление вектора
называется гиромагнитным отношением спиновых моментов. Проекция собственного магнитного момента на направление вектора 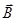 может принимать только одно из следующих двух значений
может принимать только одно из следующих двух значений 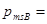 ±еħ/2m=
±еħ/2m= 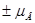 , где ħ=
, где ħ= 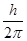 , h – постоянная Планка,
, h – постоянная Планка, 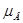 - магнетон Бора, являющийся единицей магнитного момента электрона. Общий магнитный момент атома (молекулы)
- магнетон Бора, являющийся единицей магнитного момента электрона. Общий магнитный момент атома (молекулы) 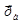 равен векторной сумме магнитных моментов (орбитальных и спиновых) электронов:
равен векторной сумме магнитных моментов (орбитальных и спиновых) электронов: 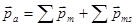 .
.
Диа – и парамагнетизм. Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент, т.е. намагничиваться.

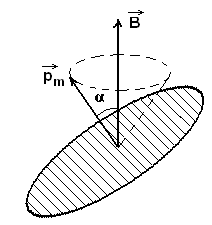
Рис.29
Если орбита электрона ориентирована относительно вектора 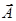 внешнего поля произвольным образом, составляя с ним ےα, то орбита и вектор
внешнего поля произвольным образом, составляя с ним ےα, то орбита и вектор 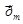 придут во вращение, которое называется прецессией (движение волчка). Прецессионное движение эквивалентно току. Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества, которое накладывается на внешнее магнитное поле и внутри магнетика образуется результирующее магнитное поле.
придут во вращение, которое называется прецессией (движение волчка). Прецессионное движение эквивалентно току. Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества, которое накладывается на внешнее магнитное поле и внутри магнетика образуется результирующее магнитное поле.
Диамагнетики – это такие вещества, в которых уменьшается магнитное поле. Для них магнитная проницаемость немного меньше 1 составляет μ ≈ 0,999935. (Объясняется действием правила Ленца). Диамагнетизм свойственен всем веществам.
Парамагнетики – вещества, в которых увеличивается магнитное поле при действии внешнего поля, для них μ больше 1, например, μ ≈ 1,00047. К парамагнетикам относятся редкоземельные элементы: Pt, Al, CuSO4 и т.д. Объясняется ориентацией орбитальных и спиновых магнитных моментов атомов в магнитном поле. При прекращении действия внешнего магнитного поля ориентация разрушается тепловым движением атомов и парамагнетик размагничивается. Магнитная проницаемость парамагнетиков превышает таковую для диамагнетиков.
Для количественного описания намагничивания магнетиков вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объема магнетика:
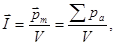 (79) где
(79) где 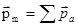 - магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул. Вектор результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля
- магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул. Вектор результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля 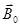 и поля микротоков
и поля микротоков 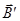 (молекулярных токов) :
(молекулярных токов) : 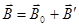 , отсюда
, отсюда 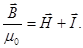 В несильных полях намагниченность пропорциональна напряженности поля, вызывающего намагничивание, т.е.
В несильных полях намагниченность пропорциональна напряженности поля, вызывающего намагничивание, т.е. 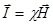 , где χ –магнитная восприимчивость вещества. Для диамагнетиков она отрицательна, для парамагнетиков – положительна. Из вышеприведенных формул:
, где χ –магнитная восприимчивость вещества. Для диамагнетиков она отрицательна, для парамагнетиков – положительна. Из вышеприведенных формул: 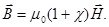 Здесь
Здесь 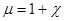 , используя эту формулу придем к известной формуле
, используя эту формулу придем к известной формуле 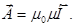
Явление электронного парамагнитного резонанса было открыто в Казани в 1945 году ученым Е.К.Завойским, сотрудником Казанского университета. Сущность явления заключается в резонансном поглощении высокочастотного электромагнитного поля при его воздействии на парамагнитное вещество, которое находится в постоянном магнитном поле. При этом частота Ларморовой процессии спинов электронов совпадает с частотой внешнего электромагнитного поля и электрон поглощает эту энергию.
Магнитные моменты ядер атомов значительно слабее магнитных моментов электронов, поэтому ядерный магнитный резонанс был открыт позже, чем электронный, 1949 году в США. Процесс аналогичен электронному, но получил более широкое применение для исследования веществ. Вершиной этого применения является создание ЯМР – томографов.
Ферромагнетики. К ним относятся: железо, кобальт, никель, гадолиний, их сплавы и соединения. μ>>1, составляет несколько тысяч.
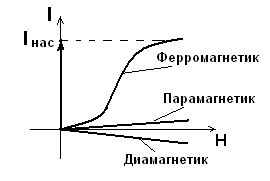
Рис.30
Iнас – магнитное насыщение.
При насыщении ориентируется все большее количество магнитных моментов.
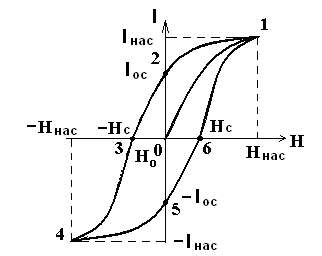
Рис.31
Характерной особенностью ферромагнетиков является то, что для них зависимость I от Н (а следовательно В от Н) имеет вид петли, которая получила название петли гистерезиса: 0 – размагниченный; 1 – насыщение ( 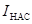 ); 2 – остаточная намагниченность (
); 2 – остаточная намагниченность ( 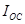 ), постоянные магниты; 3 – размагничивание (
), постоянные магниты; 3 – размагничивание ( 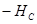 – коэрцитивная сила); дальше – повторяется.
– коэрцитивная сила); дальше – повторяется.
Ферромагнетики с малой коэрцитивной силой называются 1)мягкими, а с большой коэрцитивной силой – 2)жесткими. Первые применяются для сердечников трансформаторов и электрических машин (двигателей и генераторов), вторые – для постоянных магнитов. Точка Кюри – температура, при которой ферромагнетик теряет магнитные свойства и превращается в парамагнетик. Процесс намагничивания ферромагнетиков сопровождается изменением их линейных размеров и объема. Это явление получило название магнитострикция. Ферромагнетики имеют доменную структуру: микроскопические объемы, в которых магнитные моменты ориентированы одинаково. В ненамагниченном состоянии магнитные моменты доменов направлены хаотично и результирующее поле равно нулю. При намагничивании ферромагнетика магнитные моменты доменов скачкообразно поворачиваются и устанавливаются вдоль поля и ферромагнетик намагничивается. Как только сориентируются все домены, так намагниченность достигает насыщения. При остаточной намагниченности ( 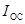 ) – ориентированы часть доменов.
) – ориентированы часть доменов.
Существуют антиферромагнетики (соединения MnO, MnF2, FeO, FeCl2).
В последнее время большое значение приобрели ферриты – полупроводниковые ферромагнетики, химические соединения типа 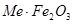 , где Ме – ион двухвалентного металла (Mn, Co, Ni, Cu, Zn, Cd, Fe). Они обладают заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением (в миллионы раз больше чем у металлов). Нашли широкое применение в электротехнике и радиотехнике.
, где Ме – ион двухвалентного металла (Mn, Co, Ni, Cu, Zn, Cd, Fe). Они обладают заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением (в миллионы раз больше чем у металлов). Нашли широкое применение в электротехнике и радиотехнике.
Лекция 10.
3.3 (2 час) Электромагнитная индукция. Закон Фарадея. Правило Ленца. Индуктивность. Самоиндукция. Плотность энергии магнитного поля. Взаимоиндукция. Трансформатор.
Опытами Ампера было показано, что около проводников с токами образуется магнитное поле, т.е. «электричество превращается в магнетизм». В то время ряд ученых задались вопросом, «а нельзя ли наоборот магнетизм превратить в электричество?». Этим же вопросом в 1821 году задался М.Фарадей и через 10 лет 29 августа 1831 года ему это удалось. Он открыл явление электромагнитной индукции – явление возникновения индукционного тока в замкнутом проводящем контуре при всяком изменении внешнего магнитного поля. Два случая: Опыт I. Если в замкнутый на гальванометр соленоид вдвигать и выдвигать постоянный магнит, то в момент его движения в цепи возникает электрический ток, называемый индукционным. Опыт II. Концы одной из двух катушек, вставленных одна в другую, подключаются к гальванометру, а через другую катушку пропускают ток. Отклонение стрелки гальванометра наблюдается в моменты включения и выключения тока, в моменты его увеличения или уменьшения, при перемещении катушек относительно друг друга.
Закон электромагнитной индукции Фарадея:
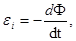 (80) где
(80) где 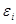 - ЭДС индукции, В,
- ЭДС индукции, В,
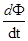 - скорость изменения магнитного потока,
- скорость изменения магнитного потока, 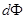 - изменение магнитного потока, Вб за время dt (с). Знак «-» указывает на Правило Ленца: индукционный ток в катушке всегда имеет такое направление, при котором его магнитное поле препятствует всякому изменению внешнего магнитного поля, вызывающего этот ток.
- изменение магнитного потока, Вб за время dt (с). Знак «-» указывает на Правило Ленца: индукционный ток в катушке всегда имеет такое направление, при котором его магнитное поле препятствует всякому изменению внешнего магнитного поля, вызывающего этот ток.
При вращении проводящей рамки в магнитном поле, в рамке возникает переменная ЭДС в соответствии с формулой 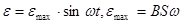 (или через косинус), здесь
(или через косинус), здесь 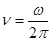 =50 Гц – частота промышленного переменного тока, используемого в России.
=50 Гц – частота промышленного переменного тока, используемого в России.
Вихревые токи (токи Фуко) – это токи, возникающие в массивных проводниках. Используются: в индукционных печах для нагрева и плавки металлов. Для их уменьшения сердечники трансформаторов и электрических машин набирают из пластин. При высокочастотных токах в линейных проводниках возникает скин – эффект – выталкивание тока на поверхность проводника. На этом основан метод поверхностной закалки металлов.
Явление возникновения индукционного тока (или ЭДС самоиндукции) в том же самом проводнике, в котором меняется основной ток, называется явлением самоиндукции:
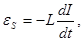 (81) здесь
(81) здесь 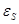 - ЭДС самоиндукции, В,
- ЭДС самоиндукции, В,
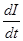 - скорость изменения основного тока,
- скорость изменения основного тока, 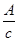 ,
,
L – индуктивность проводника (катушки).
«-» указывает на правило Ленца, 1 Гн = 1 Вб/A = 1 B·c/A.
Индуктивность бесконечно длинного соленоида:
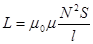 , (82) где μ – магнитная проницаемость вещества, ед,
, (82) где μ – магнитная проницаемость вещества, ед,
μ0 – магнитная постоянная вакуума, 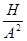 .
.
Взаимная индукция.
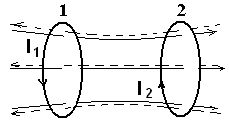
Рис.32
Если ток 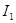 изменяется, то в контуре 2 индуцируется ЭДС
изменяется, то в контуре 2 индуцируется ЭДС 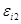 за счет изменения магнитного потока
за счет изменения магнитного потока 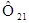 , созданного током в первом контуре и пронизывающего второй:
, созданного током в первом контуре и пронизывающего второй: 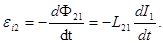 Аналогично, если ток протекает по контуру 2 и изменяется, то ЭДС
Аналогично, если ток протекает по контуру 2 и изменяется, то ЭДС 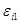 будет:
будет: 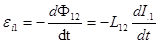 . Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимоиндукцией. Коэффициенты
. Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимоиндукцией. Коэффициенты 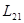 и
и 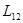 называются взаимной индуктивностью контуров. Как показывают расчеты
называются взаимной индуктивностью контуров. Как показывают расчеты 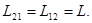 Коэффициент взаимной индуктивности (L) зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей среды. Так, если контуры имеют число витков
Коэффициент взаимной индуктивности (L) зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей среды. Так, если контуры имеют число витков 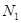 и
и 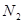 и связаны замкнутым сердечником с магнитной проницаемостью μ, площадью S и длиной l, то коэффициент взаимоиндукции будет:
и связаны замкнутым сердечником с магнитной проницаемостью μ, площадью S и длиной l, то коэффициент взаимоиндукции будет: 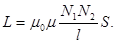
Трансформаторы – устройства предназначенные для повышения или понижения напряжения переменного тока. Работа основана на явлении взаимной индукции. Впервые трансформаторы были сконструированы русскими учеными П.Н.Яблочковым и И.Ф.Усагиным.
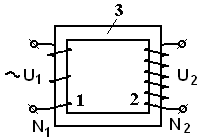
Рис.33
Простейший трансформатор устроен следующим образом: две обмотки (1 и 2) (первичная и вторичная) насажены на железный сердечник (3). Первичная обмотка подключена к источнику тока, а ко вторичной обмотке может быть подключена к нагрузке. Числа витков первичной и вторичной обмоток соответственно 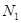 и
и 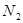 , ЭДС -
, ЭДС - 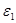 и
и 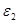 , В результате действия взаимной индукции при подключении первичной обмотки к источнику переменного тока, будет выполняться соотношение:
, В результате действия взаимной индукции при подключении первичной обмотки к источнику переменного тока, будет выполняться соотношение: 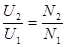 .
.
Если же подключить нагрузку, то 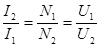 , а мощности
, а мощности 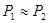 . Потери энергии составляют (2-4)%. Если
. Потери энергии составляют (2-4)%. Если 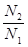 >1, то трансформатор называется повышающим и наоборот при
>1, то трансформатор называется повышающим и наоборот при 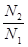 <1 – понижающим.
<1 – понижающим.
Энергия магнитного поля. Магнитное поле, образуемое электрическим током, обладает энергией. Энергия магнитного поля равна работе, которая затрачивается током на создание этого поля:
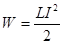 или (83)
или (83)
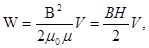 здесь (84)
здесь (84)
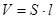 - объем соленоида.
- объем соленоида.
Объемной плотностью энергии называется 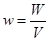 , тогда
, тогда 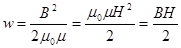 .
.
Таблица. Сравнение величин электрического и магнитного полей
| Электрическое поле | Формулы и обозначения | Магнитное поле | Формулы и обозначения |
| Точечный заряд | q, Q 
| Элемент проводника с током | Idl |
| Взаимодействие точечных зарядов | 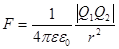
| Взаимодействие токов | 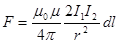
|
| Электрическая постоянная | 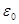
| Магнитная постоянная | 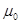
|
| Силовая характеристика электрического поля | 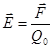
| Силовая характеристика магнитного поля | 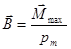
|
| Принцип суперпозиции | 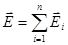
| Принцип суперпозиции | 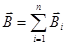
|
| Поляризованность | 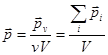
| Намагниченность | 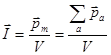
|
| Электроемкость | 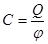
| Индуктивность катушки | 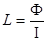
|
| Энергия заряженного конденсатора | 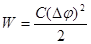
| Энергия катушки с током | 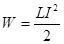
|
| Объемная плотность энергии | 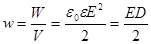
| Объемная плотность энергии | 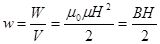
|
| Диэлектрическая проницаемость | Ε | Магнитная проницаемость | μ |
Поток вектора 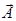 через поверхность S через поверхность S
| 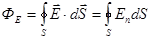
| Поток вектора 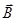 через поверхность S через поверхность S
| 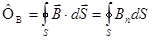
|

Лекция 11.
Образование р- n переходов. Диоды. Транзисторы.
При контакте двух полупроводников р- и n- типов образуется запирающий слой. Такое устройство называется полупроводниковым диодом. Используется для выпрямления переменного электрического тока.
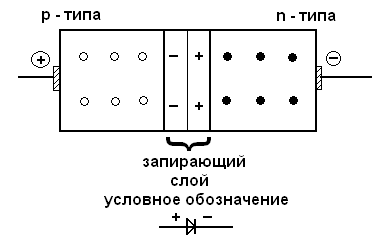
Рис.37
Односторонняя проводимость диодов
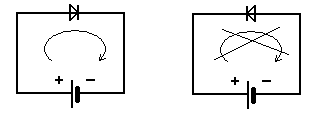
Рис.38
Вольтамперная характеристика диода
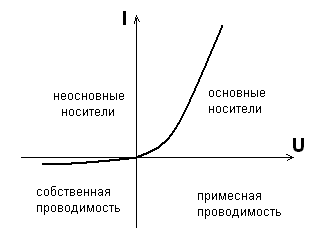
Рис.39
Транзистор предназначен для усиления электрического тока и для элементов памяти ЭВМ. Коэффициент усиления транзистора 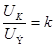 .
.
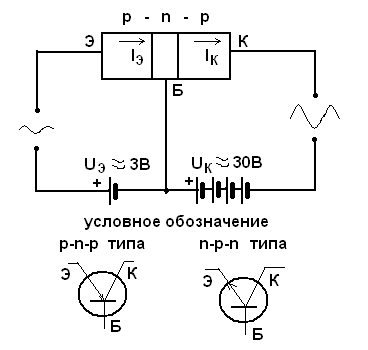
Рис.40
Интегральные схемы – сверхминиатюрные электронные устройства, состоящие из большого количества элементов. Взяв за основу элемент керамики или полупроводниковый кристалл, на него на молекулярном уровне производят напыление электронных устройств и связей между ними: транзисторов, их сочетаний (триггеров), сопротивлений, катушек и т.д. В результате такой обработки в объеме образуется сложная сеть микроячеек, обладающих определенным комплексом свойств. Такие схемы имеют твердую оболочку и они называются интегральными схемами или большими интегральными схемами (БИС). Такие схемы используются в современных компьютерах и другой вычислительной технике. Интегральные схемы отличаются высокой прочностью и надежностью, очень малым расходом энергии и исключительно малым объемом.
Лекция 12.
4.2. (0,5 часов) Токи в газах. Ионизация газов. Газоразрядная плазма. Движение заряженных частиц в электрических и магнитных полях. Циклотрон. Масс – спекрометр. Электронный микроскоп.
Газы при не очень высоких температурах и при давлениях, близких к атмосферному, являются хорошими изоляторами. Это объясняется тем, что газы при обычных условиях состоят из нейтральных атомов и молекул и не содержат свободных зарядов. Газ становится проводником, если часть его молекул ионизируется, т.е. произойдет расщепление нейтральных атомов и молекул на ионы и свободные электроны. Ионизация атомов газов происходит под действием ионизаторов (например, пламя свечи, свет и др.). Прохождение тока через газы называется газовым разрядом. Энергия, необходимая для того чтобы вызвать выбивание электрона из атома, т.е. чтобы превратить его в ион, называется энергией ионизации, значение которой для различных атомов лежат в пределах 4-25 эВ. Процесс, обратный ионизации, называется рекомбинацией. Разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным. Это происходит в результате процесса ударной ионизации.
Виды электрического разряда в газах: 1) тлеющий разряд (в трубке при пониженном давлении, ЛДС, неоновые лампы, рекламные трубки и др.); 2) искровой разряд (  ), распознается по искре и характерному треску (молния, искрение одежды и др.). Используется для воспламенения горючего в ДВС, предохранения ЛЭП от молний (искровые разрядники), искровая обработка металлов (резание, сверление); 3) дуговой разряд (дуга открыта В.В.Петровым). Применяется: для сварки и резки металлов, освещения в мощных прожекторах, в дуговых лампах с ртутными электродами и кварцевым стеклом, как источник мощного ультрафиолетового излучения; 4) коронный разряд – образование искрения и потрескивания на проводах, имеющих высокое напряжение и малый диаметр. Используется в электрофильтрах для очистки газов. Применяется при нанесении красочных и порошковых покрытий.
), распознается по искре и характерному треску (молния, искрение одежды и др.). Используется для воспламенения горючего в ДВС, предохранения ЛЭП от молний (искровые разрядники), искровая обработка металлов (резание, сверление); 3) дуговой разряд (дуга открыта В.В.Петровым). Применяется: для сварки и резки металлов, освещения в мощных прожекторах, в дуговых лампах с ртутными электродами и кварцевым стеклом, как источник мощного ультрафиолетового излучения; 4) коронный разряд – образование искрения и потрескивания на проводах, имеющих высокое напряжение и малый диаметр. Используется в электрофильтрах для очистки газов. Применяется при нанесении красочных и порошковых покрытий.
Плазма – четвертое состояние вещества, состоящее из ионов и электронов. Различают высокотемпературную (электрический разряд в газах) и низкотемпературную (металлы и др.).
Электрический ток в вакууме – движение заряженных частиц в электрическом поле. Для создания тока необходимо впрыснуть в вакуум заряженные частицы. Эти частицы – электроны. В зависимости от способа освобождения электронов различают термоэлектронную, фотоэлектронную, вторичную электронную и автоэлектронную эмиссию.
Схема масс – спектрометра
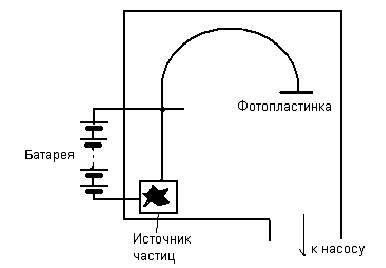
Рис.42
По радиусу движения частицы определяют отношение заряда частицы к массе: 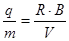 .
.
В электронном микроскопе в качестве частиц используют электроны (вместо света). Их фокусировку обеспечивают с помощью магнитных полей, которые создают специальные катушки.
Циклотрон – ускоритель элементарных частиц в магнитном поле под действием переменного электрического тока.
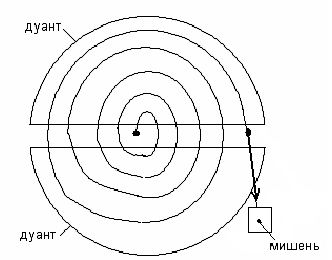
Рис.43
Лекция 13.
4.3. (0,5 часа) Токи в электролитах, Закон Фарадея. Электролитическая диссоциация. Химические источники тока.
Явление разделения нейтральных молекул на положительные и отрицательные ионы при растворении веществ в жидкостях называется электролитической диссоциацией. При подаче напряжения на электроды в электролите возникает электрический ток.
В химических источниках тока, как было рассмотрено в п.2.1 (закон Ома для участка цепи), происходит взаимодействие химических веществ с одним из электродов, который заряжается отрицательно, а раствор заряжается положительно. Такие источники дают ЭДС от 1,2 до 1,6 В.
Электролиз – явление выделения вещества на электродах, связанное с окислительно – восстановительными реакциями.
Применение электролиза: 1. Гальваностегия – покрытие изделий из металла другими металлами гальваническим методом. 2. Гальванопластика - получение рельефных копий. 3. Получение чистых металлов (алюминия, меди0 и др.
Законы электролиза Фарадея.
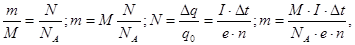 отсюда закон Фарадея
отсюда закон Фарадея
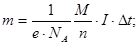 (86)
(86)
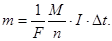 (87)
(87)
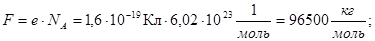
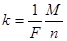 - электрохимический эквивалент; (88)
- электрохимический эквивалент; (88)
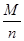 - химический эквивалент.
- химический эквивалент.
Формулировка (76) – электрохимические эквиваленты веществ пропорциональны их химическим эквивалентам.
Второй вид закона Фарадея: 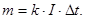 (89)
(89)
Лекция 14.
Лекция 15
5.4. Цепь переменного тока с R , L и С.
Так было, когда мы U брали за основу. Здесь все значения максимальные. От них можно перейти к действующим.
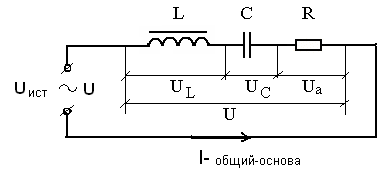
Рис.50
При последовательном соединении 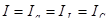
Основа – U, Основа – Iобщий , складывая 1), 2) и 3)
так было ранее так должно быть получим:
сейчас
( по схеме рис.50)
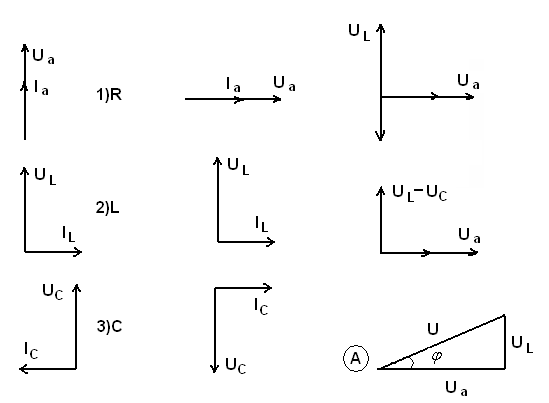
Рис.51
( А) – треугольник напряжений. Можно найти стороны. φ – сдвиг фаз между током в цепи (i) и напряжением(u) в источнике (розетке). 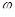 <
< 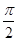 .
.
Если в треугольнике (А) стороны поделить на R, то получим (Б) – треугольник сопротивлений, подобный А, из которого получим закон Ома для цепи переменного тока с R, L и С.
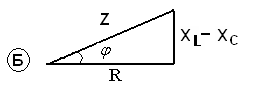
Рис.52
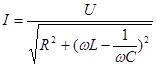 , или (107)
, или (107)
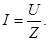 (108)
(108)
Если у треугольника (А) стороны умножить на I ,то получим треугольник мощностей (В).
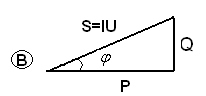
Рис. 53
Здесь Р – активная мощность (Вт),
Q – реактивная мощность (ВАр),
S – полная мощность (ВА).
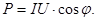 (109) cosφ – коэффициент мощности.
(109) cosφ – коэффициент мощности.
Добиваются снижения φ и увеличения cosφ – на предприятиях.
Обобщения теории Максвелла.
В 60-х годах 19-века Д.К.Максвелл, основываясь на идеях Фарадея об электрическом и магнитном полях, обобщил законы, установленные экспериментальным путем, и разработал теорию единого электромагнитного поля.
Математическим выражением теории Максвелла служат четыре уравнения Максвелла, которые принято записывать в двух формах: интегральной и дифференциальной. Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей. Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. Дифференциальные уравнения получают из интегральных с помощью теоремы Гаусса и теоремы Стокса.
6.1. Система уравнений Максвелла в дифференциальной форме:

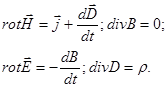
6.2. Уравнения Максвелла в интегральной форме.
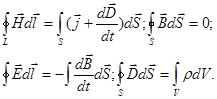

Связь величин:
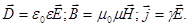
Если поля стационарны, то Е = const и В = const.
Уравнения Максвелла примут вид:
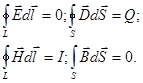
6.3. Уравнение волны:
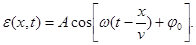
Резерв времени – 4 часа.
Формулы
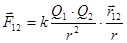 ; ;
| 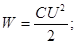
| 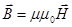 . .
|
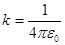 . .
| 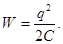
| 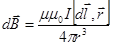 . .
|
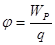 ; ; 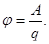
| 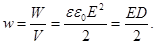
| 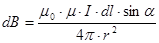 . .
|
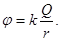
| 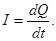
| 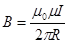 . .
|
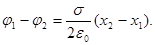
| 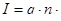 v v 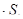
| 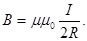
|
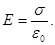
| 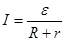 . .
| 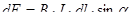 . .
|
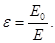
| 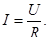
| 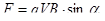
|
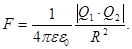
| 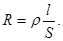
| 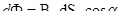
|
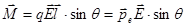 . .
| 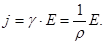
| 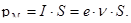
|
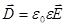 ; ; 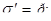
| 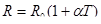 . .
| 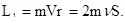
|
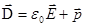 ; ; 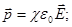
| 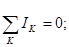 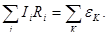
| 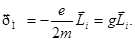
|
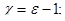
| 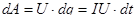 . .
| 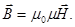
|
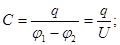
| 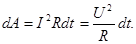
| 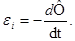
|
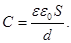
| 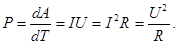
| 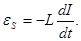
|
| Параллельное соединение конденсаторов:
| Законы последовательного соединения проводников: 1) 2) 4) | 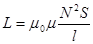 . .
|
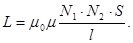
| ||
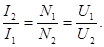
| ||
| Последовательное соединение конденсаторов:
| Законы параллельного соединения проводников: 1) 2) 3) 4) | 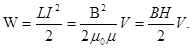
|
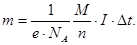
| ||
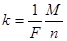 . .
| ||
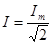 ; ; 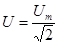 . .
| 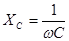 ; ; 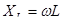 . .
| 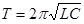 . .
|
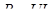 . .
| 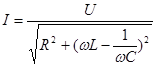 . .
| Уравнения Максвелла в дифференциальной форме:
|
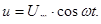
| 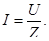
| |
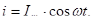
| 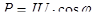
|
Основная литература:
1. Савельев И.В. Курс общей физики т. 2, М.:Наука,1999,340с.
2.Трофимова Т.И. Курс физики: учебное пособие для вузов – М.: «Академия»,2007,560с.
3. Детлаф А.А.,Яворский Б.М. Курс физики: учебное пособие для вузов – М.: «Высшая школа»,2001,718с.
Физика.
Курс лекций, II семестр, 34 часа
III, IV. Электричество и магнетизм
| Оглавление Лекция 1. 1. Электростатика. 1.1. Электрический заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Потенциал. Разность потенциалов. | 4 4 |
| Лекция 2. 1.2. Диэлектрики в электростатическом поле. Диполь. Дипольный момент. Вектор поляризации. Электростатическая теорема Гаусса. Вектор электрической индукции. Уравнение Пуассона. Условия на границе раздела двух сред. | 7 |
| Лекция 3. 1.3. Проводники в электростатическом поле. Распределение зарядов на проводнике. Электрическое поле внутри и вне проводника. Электростатическая защита. | 10 |
| Лекция 4. 1.4. Электрическая емкость. Конденсаторы. Энергия электрического поля. Плотность энергии электростатического поля. | 12 |
| Лекция 5. 2. Постоянный электрический ток. 2.1. Сила и плотность тока. Закон Ома для участка цепи и замкнутого контура. Сторонние силы. Электродвижущая сила. Закон Ома в дифференциальной форме. | 14 14 |
| Лекция 6. 2.2. Разветвление электрической цепи. Правила Кирхгофа. 2.3. Работа и мощность электрического тока. Закон Джоуля-Ленца. Превращение энергии в электрических цепях. | 17 19 |
| Лекция 7. 3.Магнитное поле. 3.1. Магнитное поле тока. Законы Био-Савара-Лапласа и Ампера. Сила Лоренца. Вектор магнитной индукции. Поток вектора магнитной индукции через замкнутую поверхность. Теорема о циркуляции вектора магнитной индукции. | 21 |
| Лекция 8. Магнитное поле прямого тока. Магнитное поле в центре кругового проводника с током. Взаимодействие двух проводников. Сила Лоренца. Поток вектора магнитной индукции. | 23 |
| Лекция 9. 3.2. Магнитные свойства вещества. Молекулярные токи. Диа -, пара- и ферромагнетики. Вектор намагниченности. Магнитная восприимчивость и магнитная проницаемость. Представление о ядерном магнитном резонансе и электронном парамагнитном резонансе. | 26 |
| Лекция 10. 3.3. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Индуктивность. Самоиндукция. Плотность энергии магнитного поля. Взаимоиндукция. Трансформатор. | 29 |
| Лекция 11. 4. Электронные и ионные явления. 4.1. Электропроводность твердых тел. Зависимость сопротивления металлов от температуры. Сверхпроводимость. Полупроводники. Эффект Холла. Электронная и дырочная проводимости, p – n переходы. Диоды, транзисторы, интегральные схемы. | 33 |
| Лекция 12. 4.2. Токи в газах. Ионизация газов. Газоразрядная плазма. Движение заряженных частиц в электрических и магнитных полях. Циклотрон. Масс-спектрометр. Электронный микроскоп. | 36 |
| Лекция 13. 4.3. Токи в электролитах, Закон Фарадея. Электролитическая диссоциация. Химические источники тока. 4.4. Контактные явления. Работа выхода электронов. Контактная разность потенциалов. Термоэлектронная эмиссия. | 38 39 |
| Лекция 14. 5. Переменный электрический ток. | |
| Лекция 15. 5.4. Цепь переменного тока с R, L и С. 6. Обобщения теории Максвелла. | 39 |
| Формулы. | 47 |
Лекция 1.
Электростатика
1.1. (2 часа). Электрический заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Потенциал. Разность потенциалов.
Существуют два рода зарядов: 1)положительные и 2)отрицательные. Положительные заряды образуются на стеклянной палочке, потертой о шелк, а отрицательные заряды образуются на каучуковой палочке, потертой о мех. Опытным путем (1910 – 1914) американский физик Р.Милликен показал, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда ( 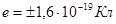 ). Электрон (
). Электрон ( 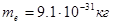 ) и протон (
) и протон ( 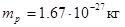 ) являются соответственно носителями элементарных отрицательного и положительного зарядов. Все тела способны электризоваться, т.е. получать избыточный электрический заряд. Электризация может осуществляться различными способами: соприкосновением (трением), электростатической индукцией (наведением) и др. При электризации электризуются оба тела: одно – положительно, другое – отрицательно. Положительная электризация объясняется недостатком электронов в теле, отрицательная – их избытком. В природе выполняется закон сохранения зарядов. В зависимости от концентрации свободных зарядов все вещества делятся на 1)проводники, 2)диэлектрики и 3)полупроводники. Единицей электрического заряда является кулон (Кл). Кулон – это такой заряд, который проходит через поперечное сечение проводника при силе тока 1А за время 1с.
) являются соответственно носителями элементарных отрицательного и положительного зарядов. Все тела способны электризоваться, т.е. получать избыточный электрический заряд. Электризация может осуществляться различными способами: соприкосновением (трением), электростатической индукцией (наведением) и др. При электризации электризуются оба тела: одно – положительно, другое – отрицательно. Положительная электризация объясняется недостатком электронов в теле, отрицательная – их избытком. В природе выполняется закон сохранения зарядов. В зависимости от концентрации свободных зарядов все вещества делятся на 1)проводники, 2)диэлектрики и 3)полупроводники. Единицей электрического заряда является кулон (Кл). Кулон – это такой заряд, который проходит через поперечное сечение проводника при силе тока 1А за время 1с.
Закон Кулона. Закон взаимодействия неподвижных точечных зарядов экспериментально установлен в 1785 г. Ш.Кулоном с помощью крутильных весов, подобных тем, которые использовались Г.Кавендишем для определения гравитационной постоянной ( ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет). Точечный заряд – это такой заряд, который сосредоточен на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других зарядов. Сила взаимодействия (F) между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна величинам этих зарядов (Q1 и Q2) и обратно пропорциональна квадрату расстояния между ними 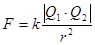 (1) в векторной форме:
(1) в векторной форме: 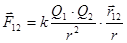 ; (2) где
; (2) где 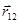 - радиус вектор, соединяющий заряд
- радиус вектор, соединяющий заряд 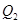 с зарядом
с зарядом 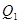 ;
; 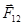 - действует на заряд 1.
- действует на заряд 1. 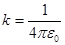 - коэффициент пропорциональности,
- коэффициент пропорциональности, 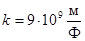 ;
; 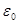 -электрическая постоянная вакуума,
-электрическая постоянная вакуума, 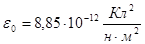 или (
или ( 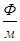 ), фарад – единица электроемкости. Точность закона проверена в большом интервале расстояний.
), фарад – единица электроемкости. Точность закона проверена в большом интервале расстояний.
Напряженностью электростатического поля в данной точке называется величина, равная отношению силы, действующей на положительный пробный заряд, помещенный в данную точку поля, к величине этого заряда.
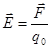 ; (3) для точечного заряда
; (3) для точечного заряда 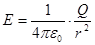 . (4) Вектор
. (4) Вектор 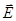 направлен в ту же сторону, что и сила.
направлен в ту же сторону, что и сила.

Рис.1
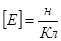 ; Линия напряженности – линия, касательная к которой в каждой точке совпадает с направлением напряженности в данной точке.
; Линия напряженности – линия, касательная к которой в каждой точке совпадает с направлением напряженности в данной точке.
Напряженность поля от нескольких зарядов равна векторной (геометрической) сумме напряженностей, созданных отдельными зарядами.
Поток вектора напряженности: 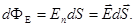

Единица потока вектора напряженности электрического поля - вольт·метр (В·м).
Потенциал электростатического поля.
Поля, в которых работа силы (созданной полем) по замкнутой траектории равна нулю называются потенциальными. Это – электростатическое и гравитационное поля.

Рис.2
Определение I : Потенциалом поля в данной точке называется величина, равная отношению потенциальной энергии заряда в этой точке, к величине этого заряда.
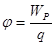 . (5)
. (5)
Определение II : Потенциалом поля в данной точке называется величина, равная отношению работы по перемещению положительного пробного заряда из данной точки поля в бесконечность, к величине этого заряда.
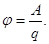 (6)
(6)
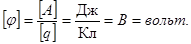
Разность потенциалов. Напряжение.
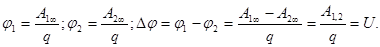
Разностью потенциалов двух точек поля называется величина, равная отношению работы по перемещению положительного пробного заряда из одной точки поля в другую, к величине этого заряда.
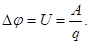 (7)
(7)
Потенциал, созданный шаром (равномерно заряженным по поверхности)
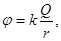
где 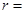 от
от 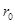 до
до 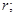
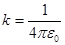 .
.
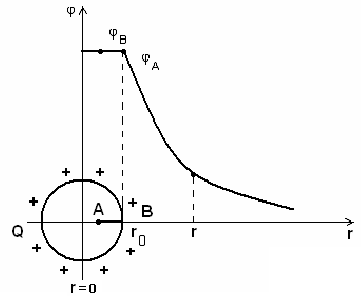
Рис.3
Поле равномерно заряженной плоскости:
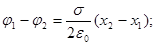 (8)
(8)
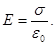 (9)
(9)
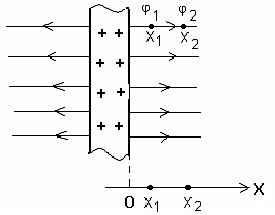
Рис.4
Поле равномерно заряженного бесконечного цилиндра:
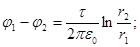 (10)
(10)
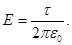 (11)
(11)
Лекция 2
1.2. (2 часа) Диэлектрики в электростатическом поле. Диполь. Дипольный момент. Вектор поляризации. Электростатическая теорема Гаусса. Вектор электрической индукции. Уравнение Пуассона. Условия на границе раздела двух сред.
- Два вида диэлектриков:
( 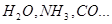 ) (
) ( 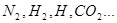 )
)
1. Полярные – это такие диэлектрики, 2. Неполярные – это такие диэлектрики,
у которых центры положительных и у которых центры положительных и от-
отрицательных зарядов внутри моле- рицательных зарядов совмещены (ε <3).
кул разделены (ε >3).


противоположных по знаку электри- совмещен с центром положительного за-
ческих зарядов. ряда (ядра).
2(а). 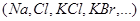 Эту группу составляют вещества, молекулы которых имеют ионное строение (ионные кристаллы). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток (разного знака). (ε >3).
Эту группу составляют вещества, молекулы которых имеют ионное строение (ионные кристаллы). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток (разного знака). (ε >3).
Поляризация диэлектриков.

Рис.5
В полярных диэлектриках диполи поворачиваются, а в неполярных и ионных – заряды смещаются.
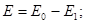
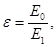 (12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
(12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
Закон Кулона:
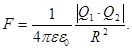 (13)
(13)

Рис.6
Электрический момент диполя: 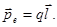 (14)
(14)
Дипольный момент: 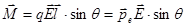 (15) или:
(15) или: 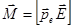 - этот вектор направлен перпендикулярно плоскости векторов
- этот вектор направлен перпендикулярно плоскости векторов 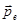 и
и 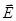 , так что из конца вектора
, так что из конца вектора 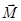 вращение от
вращение от 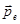 к
к 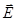 по кратчайшему пути видно происходящим против часовой стрелки.
по кратчайшему пути видно происходящим против часовой стрелки.
Поляризованностью называют дипольный момент единицы объема диэлектрика:
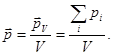 (16)
(16)
Для большинства диэлектриков (за исключением сегнетодиэлектриков) поляризованность линейно зависит от напряженности поля (Е). Если диэлектрик изотропный и 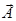 не слишком велико, то
не слишком велико, то
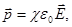 (17) где χ – диэлектрическая восприимчивость вещества:
(17) где χ – диэлектрическая восприимчивость вещества:
χ + 1 = ε, (18) величина безразмерная, причем χ >0. Поляризованность проявляется образованием на поверхности диэлектрика связанных зарядов. Поверхностная плотность ( 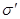 ) связанных зарядов равна поляризованности (р).
) связанных зарядов равна поляризованности (р). 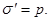 Вектор электрического смещения (поляризации) для электрически изотропной среды:
Вектор электрического смещения (поляризации) для электрически изотропной среды:
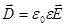 (19) или
(19) или 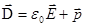 . (20)
. (20)
Единица электрического смещения - 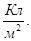 Вектором
Вектором 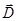 описывается электрическое поле, созданное связанными зарядами.
описывается электрическое поле, созданное связанными зарядами.
Поляризацией диэлектрика называется процесс ориентации диполей или появление под действием внешнего электрического поля ориентированных по полю диполей.
Вектор 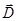 аналогично
аналогично 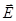 изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
Для произвольной замкнутой поверхности S поток вектора 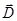 сквозь эту поверхность:
сквозь эту поверхность:
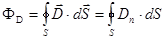 , (21) где
, (21) где 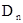 - проекция
- проекция 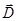 на нормаль
на нормаль 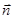 к площадке dS .
к площадке dS .
Теорема Гаусса для электростатического поля в диэлектрике:
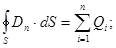 (22) или упрощенно
(22) или упрощенно 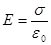 или D = σ.
или D = σ.
Для электростатического поля в вакууме дифференциальное уравнение, называемое уравнением Пуассона:
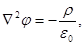 (23) где оператор Лапласа:
(23) где оператор Лапласа:
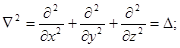 (24) ρ – объемная плотность заряда. В среде
(24) ρ – объемная плотность заряда. В среде 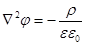 , φ – потенциал поля.
, φ – потенциал поля.
Если в среде нет свободных зарядов, то 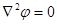 - уравнение Лапласа.
- уравнение Лапласа.
Условия на границе раздела двух сред:
ε2 > ε1

Рис.7
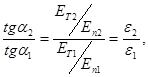 отсюда
отсюда 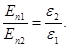 (25)
(25)
На границе двух сред нет свободных зарядов, тогда Еn2 < En1, т.к ε2 > ε1.
Лекция 3 .
1.3.(2часа) Проводники в электростатическом поле. Распределение зарядов на проводнике. Электрическое поле внутри и вне проводника. Электростатическая защита.
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. Если поле внутри проводника не было бы равно нулю, то под действием этого поля заряды пришли бы в движение без внешнего источника, что противоречит закону сохранения энергии. Равенство нулю электрического поля внутри проводника приводит к тому, что потенциал поля внутри проводника одинаков (φ = const). Поверхности, которые имеют одинаковый потенциал, называются эквипотенциальными. Отсюда следует, что в любой точке проводника любой формы в каждой его точке вектор напряженности поля на внешней поверхности перпендикулярен к этой поверхности. Если бы было не так, то под действием составляющей напряженности вдоль этой поверхности заряды пришли бы в движение, что противоречит равновесному распределению зарядов.
Если проводнику сообщить некоторый заряд, то он распределится по поверхности проводника, внутри же проводника зарядов так же не будет.
Взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью σ зарядов на его поверхности в соответствии с теоремой Гаусса будет:
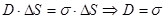 (26)
(26)
или 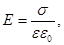 (27) где ε – диэлектрическая проницаемость вещества.
(27) где ε – диэлектрическая проницаемость вещества.
Согласно этой формулы Е и σ связаны вблизи проводника любой формы. Из формулы 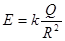 и формулы (27) вытекает, что плотность зарядов и напряженность поля на одном и том же проводнике там больше, где кривизна поверхности (1/R) больше, или R меньше.
и формулы (27) вытекает, что плотность зарядов и напряженность поля на одном и том же проводнике там больше, где кривизна поверхности (1/R) больше, или R меньше.
Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряд придут в движение и будут двигаться до поверхности проводника.

Рис.8
Эти заряды называются индуцированными. Напряженность внутри проводника будет равна нулю. Явление образования индуцированных зарядов называется электростатической индукцией. По формуле (26) электрическое смещение вблизи проводника численно равно поверхностной плотности смещенных электрических зарядов, поэтому вектор 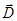 получил название вектора электрического смещения. Применение явления – электростатическая защита – густая металлическая сетка (экранирование приборов, установок, людей).
получил название вектора электрического смещения. Применение явления – электростатическая защита – густая металлическая сетка (экранирование приборов, установок, людей).
Электростатический генератор – предназначен для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт.

Рис.9. 1 – шарообразный полый проводник,
2 – изоляторы, 3 – лента из прорезиненной ткани,
4 – система остриев, 5 – заземленная пластина,
6 – источник высокого напряжения,
7 – кисточковый съемник зарядов.
Лекция 4.
1.4. (2часа). Электрическая емкость. Конденсаторы. Энергия электрического поля. Плотность энергии электростатического поля.
Понятие электроемкости уединенного проводника такое же как и для двух проводников. В этом случае электроемкостью двух проводников называется отношение заряда на одном из проводников к разности потенциалов между этими проводниками.
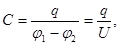 (28) где С – емкость;
(28) где С – емкость;
q – заряд;
U – разность потенциалов.
Единицы электроемкости
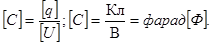
В радио: В учебниках:
1 мкФ = 10-6Ф мФ, мкФ, нФ, nФ
1nФ = 10-12Ф
Опыт

Рис.10
Электроемкость шара.
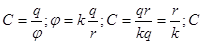 ~ r .
~ r .
Емкость земного шара 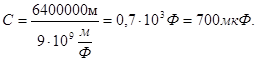 Емкость Солнца: 0,2Ф.
Емкость Солнца: 0,2Ф.
Конденсаторы – устройства для накапливания электрических зарядов, изобретались как устройства, обладающие большой емкостью.
Конденсатор – устройство, состоящее из двух пластин, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами пластин.

Рис.11 Зарядка конденсатора

Рис.12
Под зарядом конденсатора понимают заряд одной из его пластин.
Первый конденсатор – лейденская банка.
Электроемкость плоского конденсатора:
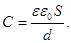 (29)
(29)
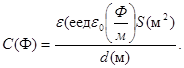 (Объяснение зависимости С от S и d).
(Объяснение зависимости С от S и d).
Измерение диэлектрической проницаемости
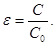 (30)
(30)
Электроемкость шарового и цилиндрического конденсатора при r >> d определяется по формуле (16).
Дата: 2019-07-24, просмотров: 334.
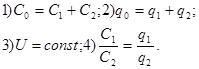
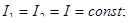
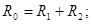 3)
3)