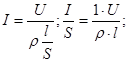
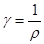- удельная электрическая проводимость, ;

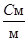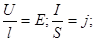
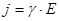 - закон Ома в дифференциальной форме.

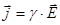 - в векторном виде.

Зависимость сопротивления от температуры.

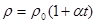 ;                                                                                                           (42)

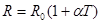,                                                                                                            (39) где ρ и ρ₀, R и R₀ – удельные сопротивления и сопротивления проводника при t и 0⁰С

α – термический коэффициент сопротивления, ;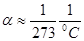

Из приведенной формулы можно получить

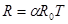,                                                                                                                  (42) здесь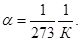

При низких температурах открыто явление сверхпроводимости.

Термосопротивления используются для термометров сопротивления.

Термисторы – термосопротивления из полупроводников.

Лекция 6.

2.2.(1 час) Разветвление электрической цепи. Правила Кирхгофа.

Непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.) довольно сложен. Эта задача более просто решается с помощью двух правил Кирхгофа (немецкий физик, 1824 – 1887). Любая точка разветвления цепи, в которой сходятся не менее трех проводников с током, называется узлом. При этом ток, входящий в узел считается положительным, а ток, выходящий из узла – отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

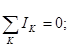                                                                                                                       (44) или непосредственно по рисунку 17:

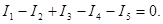
Это правило вытекает из закона сохранения заряда.

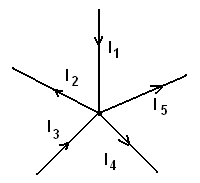
Рис.17

Второе правило Кирхгофа: в любом замкнутом контуре (произвольно выбранном в разветвленной электрической цепи) алгебраическая сумма произведений сил токов 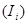 на сопротивление 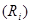соответствующих участков этого контура равна алгебраической сумме ЭДС 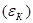, встречающихся в этом контуре:

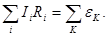                                                                                                              (45)

Если направление тока (I) совпадает с направлением обхода, то ток положителен. Если направление обхода от «минуса» к «плюсу» источника, то ЭДС положительна и наоборот.

Пример:

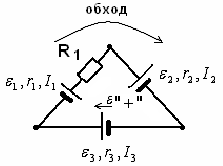
Рис.18

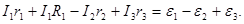
При расчете сложных цепей постоянного тока используют следующий алгоритм:

1. Выбрать произвольное направление токов на всех участках цепи; действительные направления токов определятся после решения задачи; если искомый ток получится положительным, то его направление было выбрано правильным, если отрицательным, то его истинное направление противоположно выбранному.

2. Выбрать произвольно направление обхода контура и строго придерживаться его. Записать произведения токов на сопротивления с учетом знаков и приравнять их сумме ЭДС. Составить уравнения по первому правилу Кирхгофа.

3. По этапам 1 и 2 составить столько уравнений, чтобы их число было равно числу искомых величин. В систему уравнений должны входить все сопротивления и ЭДС цепи.

В качестве примера рассмотрим схему измерительного моста Уинстона (английский физик, 1802 – 1875). Используется для определения неизвестных сопротивлений.

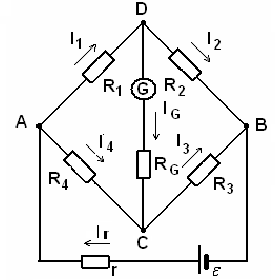Рис.19

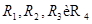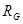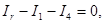
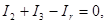
Сопротивления образуют его «плечи». Между точками А и В моста включена батарея с ЭДС ε и сопротивлением r, между точками С и Д включен гальванометр с сопротивлением . Для узлов А,В, и С, применяя первое правило Кирхгофа, получим: 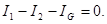(1)

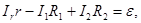
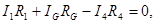
Для контуров АСВА, АСДА и АВДС можно записать: 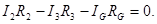(2)

Если известны все сопротивления и ЭДС, то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления 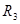 и 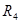 можно добиться, чтобы ток через гальванометр был равен нулю 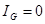, тогда из (1) получим 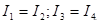(3). Тогда из (2) получим:  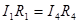и 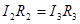 (4). Из (3) и (4) получим  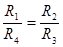или 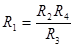(5). Тогда в случае равновесного моста  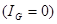при определении неизвестного (искомого) сопротивления  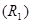ЭДС батареи, сопротивление батареи и гальванометра роли не играют.

На практике используют реохордный мостик Уинстона, где сопротивления 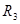 и 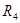 представляют собой одну длинную проволоку с большим удельным сопротивлением. Тогда формула (5) будет 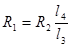. Длины  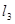и 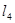 легко измеряются по шкале, а  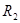всегда известно.

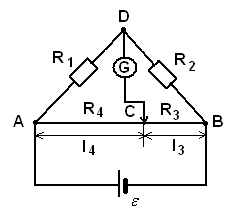
Рис.20