За время dt через сечение проводника, к которому приложено напряжение U, переносится заряд dq= I·dt, При этом силы электростатического поля (и сторонние силы) совершают работу 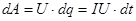                                                                                    .                                                                                                       (46)

Если из закона Ома ввести в (46) сопротивление R:

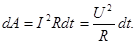                                                                                                        (47)

Это формула для работы тока. Из (47) получим мощность тока:

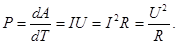                                                                                                 (48)

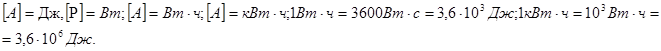
Если работа тока идет на нагревание, то

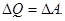                                                                                                                        (49)

Тогда количество теплоты будет определяться из (47) и (49) по закону Джоуля – Ленца

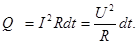                                                                                                        (50)

Закон Джоуля – Ленца широко используется в технике: русским инженером Лодыгиным изобретена лампа накаливания (1873), на нагревании проводников электрическим током основано действие электрических (нагревательных) муфельных печей, электрической дуги ( открыта русским инженером В.В.Петровым), контактной электросварки, бытовых электронагревательных приборов и т.д.

Законы соединения проводников.

1. Последовательное соединение проводников.

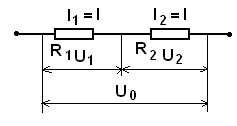
Законы:                                                 Рис.21

1)

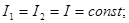
2)

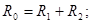
3)

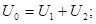
4)

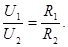
 - Где используются, недостатки, преимущества?

2. Параллельное соединение проводников.

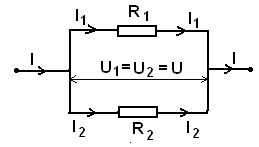
Законы:                                                   Рис.22

1)

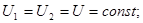
2)

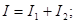
3)

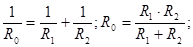
4)

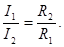
 - Где используется, преимущества, недостатки?

                                                      Лекция 7

Магнитное поле

3.1 (2часа) Магнитное поле тока. Законы Био-Савара-Лапласа и Ампера. Сила Лоренца. Вектор магнитной индукции. Поток вектора магнитной индукции через замкнутую поверхность. Теорема о циркуляции вектора магнитной индукции.

В пространстве, где протекает электрический ток и находятся постоянные магниты образуется силовое поле, называемое магнитным полем. Название «магнитное поле» возникло при наблюдении ориентации магнитной стрелки под действием этого поля.

Свойства магнитного поля: 1) Магнитное поле создается током (движущимися зарядами); 2) Магнитное поле обнаруживается по действию на электрический ток.

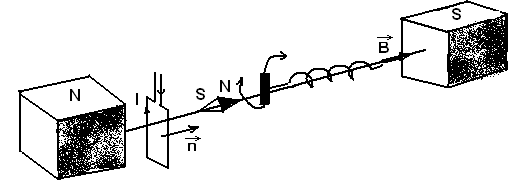
Рис.23

Изучение магнитных полей проводят с помощью 1)рамки стоком, 2)магнитной стрелки. Используют правило буравчика.

За направление магнитного поля принимают направление, в котором устанавливается 1)ось магнитной стрелки от S к N или 2)нормаль к плоскости рамки, определяемая по правилу буравчика (правого винта).

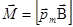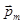Правило: за положительное направление нормали принимают направление поступательного движения винта, рукоятка которого вращается в направлении тока, протекающего в рамке. Вращающий момент, действующий на рамку: , где  - вектор магнитного момента рамки с током, 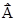- вектор магнитной индукции. Для плоского контура с током: 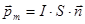, где S – площадь поверхности контура (рамки),  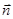- единичный вектор нормали. 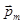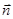(Направления  и  совпадают).

Характеристикой поля может служить магнитная индукция:

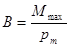                                                                                                                      (51)

Магнитной индукцией поля называется отношение максимального вращающего момента к магнитному моменту, когда нормаль к рамке перпендикулярна направлению поля. Вектор 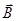может быть получен по закону Ампера и из выражения для силы Лоренца.

Линии магнитной индукции – линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции. Их направление определяется с помощью рамок с током и с помощью магнитных стрелок.

Линии магнитной индукции можно проявить с помощью магнитных стрелок. Свойства линий магнитной индукции: они всегда замкнуты, они нигде не пересекаются, они расположены там гуще, где магнитное поле сильнее, для постоянных магнитов они выходят с из северного полюса и входят в южный.

Магнитное поле – вихревое поле. Магнитных зарядов, подобных электрическим, нет.

Магнитные свойства вещества объясняются циркуляционными токами, протекающими в атомах веществ, они создают свое магнитное поле и могут поворачиваться по отношению к внешнему полю, полю макротоков. Магнитное поле макротоков описывается вектором напряженности магнитного поля .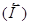

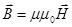,                                                                                                                (52)

где 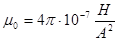 - магнитная постоянная,

μ – магнитная проницаемость среды, ед, безразмерная величина, она показывает во сколько раз магнитное поле в среде больше чем вне среды,

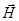 - вектор напряженности магнитного поля, ,

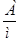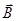 - индукция магнитного поля, .

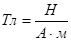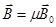,                                                                                                                  (53)

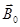 - индукция магнитного поля вне среды (вакуум),

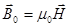 - связь  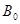и Н (индукции и напряженности).

Закон Био-Савара-Лапласа (французские ученые) получен (рис.22) для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля 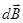, записывается в виде:

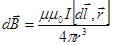,                                                                                                      (54) где 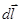- вектор по модулю равный длине dl провода и совпадающий по направлению с током,

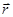 - радиус- вектор проведенный из элемента dl проводника в точку А поля,

r  – модуль радиуса –вектора .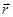

Направление 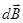 перпендикулярно  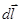и 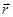, т.е. перпендикулярно плоскости, в которой они лежат.

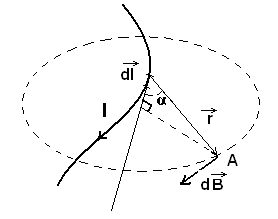
Рис.24

Модуль вектора 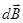 определяется выражением:

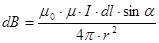.                                                                                              (55)

Для магнитного поля выполняется принцип суперпозиции: вектор магнитной индукции результирующего поля, создаваемого несколькими токами (или их элементами, а также движущимися зарядами) равен векторной сумме магнитных индукций, создаваемых этими токами (или их элементами, а также движущимися зарядами):

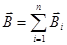.                                                                                                                 (56)

Расчет характеристик магнитного поля ( 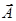 и 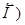по приведенным формулам в общем случае сложен.. Однако, если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа и принципа суперпозиции позволяет просто рассчитать конкретные поля.

Лекция 8

  Рассмотрим два примера:

1. Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины.

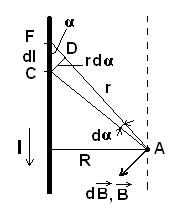
Рис.25

В произвольной точке А, удаленной от оси проводника на расстояние R. Сложение векторов 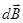 можно заменить сложением их модулей. В качестве постоянной интегрирования выбираем угол α (между 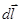и 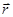), выразив через него все остальные величины.

Из рисунка:

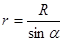,                                                                                                                  (57)

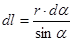.                                                                                                                (58)

Подставляя эти величины в (43) закон Био-Савара-Лапласа, получим:

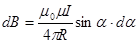.                                                                                                 (59)

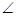α меняется от 0 до π, поэтому:

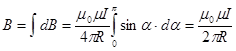.                                                                           (60)